Dictionnaire de base du vocabulaire des mathématiques C

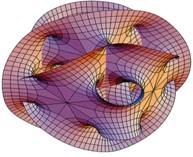
= 0, 577 215 … Constante d'Euler-Mascheroni.
Limite de la différence entre la série harmonique et le logarithme naturel.
– v. Constante d'Euler, lettres symboles
– a. Euler's constant: a mathematical constant usually denoted by the lowercase Greek letter gamma.

c = 299 792 458 m/s Célérité de la lumière dans le vide; valeur exacte.
– v. Vitesse de la lumière, lettres symboles
– a. Speed of light in vacuum or lightspeed

Aussi: vitesse de toutes les particules sans masse, des rayonnements électromagnétiques et des ondes gravitationnelles.
Valeur constante du fait de la définition du mètre: 1 m = longueur du trajet de la lumière en 1/299 792 458 seconde.

C en fonte éclaircie: est l'ensemble des nombres complexes; c'est un corps.
– v. Nombre complexe
– a. Complex numbers

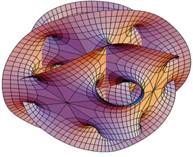Calabi-Yau (variété de -): variétés ("surfaces") particulières de dimension quatre ou plus (Exemple en illustration). Utiles pour tenter d'unifier la relativité générale et de la mécanique quantique avec la théorie des super cordes. En effet, pour assurer sa cohérence mathématique, notre espace-temps devrait posséder 6 ou 7 dimensions supplémentaires.
– a. Calibi-Yau manifold or space

Calcul: consiste à effectuer des opérations et à en donner le résultat.
– étym. mot qui vient du latin calculus, caillou .
– v. Arithmétique, compter
– v. Initiation au calcul, les quatre opérations, histoire du calcul, mots usuels du calcul
– a. Calculation, computation; the method of calculation, to learn arithmetic at school; you have to calculate the sum; etc.

Calcul mental: calcul de tête sans papier ni crayon..
– v. Calcul mental
– a. mental math: mental math is math that is done in your head, without writing or using a calculator or other device.

Calcul numérique: calcul avec seulement des nombres, par opposition à calcul littéral ou calcul algébrique.
– syn. Application numérique: calcul numérique à partir d'une formule algébrique.
– v. Calcul algébrique
– a. Evaluate expression, calculate the following expression for x=3 and z=2, replace the formula by its value;
Algebra computation, symbolic computation, computer algebra;

Calcul rapide: calcul avec des techniques, des procédés, des astuces accélérant l'obtention des résultats;
– v. Calcul rapide
– a. Fast calculation, quick calculation, maths tricks,

Calcul trigonométrique: calcul utilisant la trigonométrie
– v. Trigonométrie, identités trigonométriques
– a. Trigonometric calculation

Calculable (nombre réel -)** il est possible de formaliser un algorithme qui donne tous ses chiffres; sinon il est non-calculable.
– v. Machine de Turing et calculabilité, Oméga de Chaitin
– a. Computable number: real numbers that can be computed to within any desired precision by a finite, terminating algorithm.

Calcul infinitésimal – Calculus >>>
Calcul différentiel – Differential calculus >>>
Calcul intégral – Integration calculus >>>
Calcul vectoriel ou analyse vectorielle – Vector calculus >>>
Calcul matriciel – Matrix calculus >>>

Calcul multipartite sécurisé*: branche de la cryptographie.
– a. Secure multi-party computation ou multi-party computation (MPC)

Prenons un exemple: trois personnes et leur salaire. Ils veulent connaître le plus élevé des trois salaires, sans se révéler le salaire de chacun.

Un tiers de confiance pourrait le calculer ce maximum et le communiquer à chacun en gardant le secret des salaires.

Le but de la MPC est de se passer de ce tiers en calculant une fonction particulière basée sur des échanges messages uniquement entre eux.

Calculable: qui peut être calculé par une machine de Turing; dit-autrement: calcul qui peut être exécuté et donner une réponse en un temps fini.
– syn. théorie de la calculabilité
– v. Machine de Turing et calculabilité, Oméga de Chaitin
– a. Computable, computability theory, computable functions

Calculer une expression: réduire, développer, factoriser, simplifier.
– v. Mots usuels du calcul, techniques de base de l'algèbre,
– a. Reduce, expand, factor, simplify an expression. Algebraic manipulations, compute expressions

Calotte sphérique: portion de la sphère limitée par un plan ne passant pas par le centre.
Un plan passant par le centre forme deux demi-sphères.
– v. Calotte sphérique, segment sphérique, zone sphérique
– a. Spherical cap or spherical dome: a portion of a sphere cut off by a plane; hemisphere.

Canonique (forme -): Se dit d’un objet mathématique attaché à certaines structures de façon privilégiée.
Forme particulière d'un polynôme permettant d'étudier plus facilement la résolution des équations.
– v. Forme canonique du polynôme / Exemple
– a. Canonical form or standard form (attention: acception légèrement différent du français)

Équation canonique: équation modèle pour une famille d'équations.
– ex. L’équation Ax² + Bxy + Cy² + Dx + Ey + F = 0 est l’équation canonique de la famille d’équations du second degré à deux variables.
– v. Formes polynomiales du second degré

Forme canonique du polynôme du second degré: f(x) = a { b(x – h) }² + c

Injection canonique: si A est une partie d’un ensemble E, l’application qui à chaque élément x de A associe le même élément x considéré comme élément de E (c’est donc une application de A dans E) est appelée injection canonique de A dans E.

Base canonique: ℝ², ensemble des couples (x. y) d’éléments de ℝ, est un espace vectoriel de dimension 2, dont la base simple est constituée par l’ensemble des deux couples (0, 1) et (1, 0). Cette base est appelée base canonique de ℝ².
De même, la base constituée par les trois triplets (1, 0, 0), (0, 1, 0) et (0, 0, 1) est appelée base canonique de l’espace vectoriel ℝ³ (ensemble des triplets (x, y, z) d’éléments de ℝ).

Application canonique: si E est un ensemble sur lequel est définie une relation d’équivalence R, l’application qui à chaque élément x de E associe sa classe d’équivalence Cl(x) est appelée application canonique de E. C’est une application de E dans l’ensemble quotient E/R.

Cantor (diagonale de -)* . Outil inventé par Georg Cantor en 1891 pour démontrer que l'ensemble des nombres réels n'est pas dénombrable.
– syn. Argument de la diagonale de Cantor
– v. Diagonale de Cantor
– a. Cantor's diagonal argument

Cap: Angle compris entre l'orientation du véhicule (ligne de foi de l'avion, du bateau ...) et la direction du nord.
Cap vrai: avec le nord géographique.
Cap magnétique: avec le nord magnétique.
Cap compas: avec le nord indiqué par la boussole.
– v. Gisement, relèvement, gisement et cap, tangage et roulis
– a. Heading , Course, Drift angle

La route est égale au cap en l'absence de dérive. La dérive est due aux courants ou aux vents. Dans le cas général, la route est égale au cap plus la dérive: R = G + D.

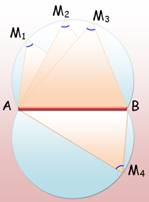Capable (arc -): l'arc capable relatifs à un angle et deux points A et B est l'arc de cercle limité par les points A et B, tel que tout point M de cet arc intercepte AB sous un angle . L'ensemble des points du plan (M_i) d'où l'on voit un segment (AB) fixé sous un angle donné est la réunion de deux arcs de cercle, les arcs capables (voir figure).
– v. Angles, angle inscrit
– a. Inscribed angle

Caractère: terme de statistique désignant l'objet sur lequel porte l'étude: la taille d'un individu, le poids d'un objet, la dépense d'une famille …
– v. Variable quantitative (terme préféré à caractère); opposée à: variable qualitative.
– v. Statistique, fréquence, distribution
– a. Quantitative variable may be continuous or discrete
qualitative variable or categorial variable

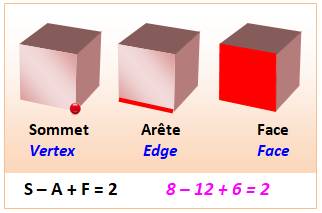
Caractère quantitatif: le prix d'un objet, la hauteur des arbres ou tout autre critère d'étude en statistique auquel on peut donner une valeur; un caractère quantitatif peut être soit discret soit continu.

Caractère qualitatif: ce sont des noms et pas des nombres; ex: les produits d'un magasin.

Caractère de divisibilité: Voir Critère de divisibilité

Caractériser des éléments mathématiques: décrire les propriétés propres à ces éléments.

Caractéristique: désigne un élément qui permet de distinguer des objets d'une même famille, de nature semblable.
– a. Characteristic

Caractéristique (d'un logarithme): partie entière d'un logarithme décimal.
La partie décimale à rajouter à la partie entière s'appelle mantisse.
– ex. log₁₀ (120) = log₁₀ (10² × 1,2) = 2 + log₁₀ (1,2) = 2 + 0,07918…
– v. Logarithme
– a. Characteristic and mantissa

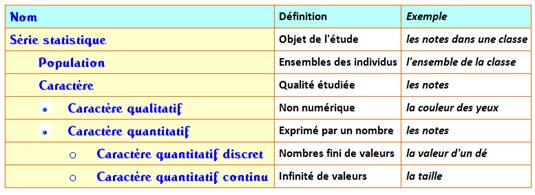Caractéristique d'Euler-Poincaré*: nombre qui caractérise une famille d'objets en topologie.
– ex. Pour le cube, comme pour tous les polyèdres convexes, cette caractéristique vaut 2 (Illustration)
– v. Caractéristique d'Euler-Poincaré
– a. Euler characteristic

Caractéristique (fonction -) ou fonction indicatrice de l'ensemble F relativement à E: elle indique si un élément x de E appartient à F (valeur 1) ou non (valeur 0).
Cette fonction qui vaut 1 o u 0 permet de résumer une fonction en une ligne plutôt que plusieurs lignes selon son domaine de valeurs.
– a. Indicator function
– ex.

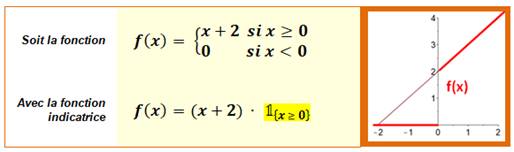Cardinal: quantité d'éléments dans un ensemble.
– v. Cardinal, Cardinaux et infini
– a. Cardinality; to have a cardinality of 5.

Cardinal (ou ordre) d'un groupe, cardinal d'un corps
– a. Order of a group, of a field

Cardinal (nombre -): qui exprime une quantité d'objets (3 pommes, 5 poires)
– ex. zéro, un, deux, trois, quatre, etc. sont des adjectifs numéraux cardinaux.
– v. Cardinaux et ordinaux, ordinal, subitisation, surcomptage
– a. Cardinal and ordinal numbers

On distingue deux sous-catégories principales de numéraux : les numéraux cardinaux utilisés pour désigner une quantité et les numéraux ordinaux utilisés pour désigner la position numérique d’un élément dans une liste.
A Cardinal Number is a number that says how many of something there are, such as one, two, three, four, five.
An Ordinal Number is a number that tells the position of something in a list, such as 1^st, 2^nd, 3^rd, 4^th, 5^th etc.
The set A = {5, 7, 9} contains 3 elements and therefore A has a cardinality of 3.

Numérosité: synonyme de cardinalité.
Aussi: quantité de chiffres d'un nombre.– v. Concept de nombre; Comment calculer le nombre de chiffres ?

Cardinal (sinus -): la fonction sinus de x divisée par x.
Utile en physique ondulatoire.
– a. Sinc function
– Développement en série et graphe:

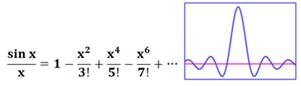
Cardioïde: trajectoire d'un point fixé à un cercle qui roule sans glisser sur un second cercle de même diamètre.
Courbe algébrique plane.
– eq. (x² + y² - ax)² = a²(x² + y²). Illustration avec a = 1, 2 et 3.
– étym. du grec cardia, cœur
– v. Champ brouté par la chèvre, le pou fractal
– a. Cardioid

Carré: rectangle dont les quatre côtés sont égaux (côtés de même longueur ou côtés isométriques); ou rectangle dont deux côtés adjacents sont égaux.
Ses quatre angles sont droits.
Quadrilatère régulier à quatre côtés.
Le carré possède huit cas de symétries: rotations de -90, 0, 90 et 180°, puis réflexions par rapport aux deux diagonales et aux deux segments milieux.
– syn. (vieilli): tétragone.
– not. □ ABCD veut dire carré de sommets A, B, C et D. (unicode: 25A1)
– v. Carré, quadrilatère, losange
– a. Square: de l’ancien français esquarre, qui a donné équerre, du latin exquadra.

Carré: opération qui consiste à multiplier un élément par lui-même.
On dit: élever au carré (nombre) ou mettre au carré (expression algébrique).
– not. un petit deux en exposant derrière l'élément.
– ex. a² = a · a; (a + b)² = a² + 2ab + b²
– v. Identités remarquables
– a. Squaring; élever au carré: to square

Racine carrée: inverse du carré: nombre qui multiplié par lui-même donne l'original
– ex. 2 est la racine carrée de 4 car 2 × 2 = 4.
– v. Racine carrée
– a. Square root

Carré d'un nombre ou carré parfait: ce nombre multiplié par lui-même.
– noté: a² (100 est le carré de 10 car 10 x 10 = 100).
– ex. 4, 9, 16, 25, 36, 49 … sont des carrés parfaits.
– v. Racine carrée, puissance, cube
– v. Carré d'un nombre, nombres sans facteur carré
– a. Square, square number, perfect square

Carré latin, gréco-latin: jeu de grille, les éléments sur une ligne ou sur une colonne doivent être différents.
– v. Carré latin, carré magique, Sudoku
– a. Latin square: an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column.

Carré magique: tableau de chiffres dont les lignes, colonnes et diagonales donnent une même somme, dite magique.
– v. Carrés magiques / Vocabulaire du carré magique
– a. Magic square

Carré diabolique: carré magique présentant de nombreuses autres fois la somme magique.
Carré panmagique, diabolique 5x5
– a. panmagic, pendiagonal magic, diabolic square

Carrés (méthode des moindres -)* méthode de lissage d'une courbe. La courbe étant définie par un nuage de points, la méthode est basée sur la minimisation de la moyenne quadratique des écarts.
– v. Régression
– a. The method of least squares

Carrelage: synonyme de dallage, de pavage, de tessellation: recouvrement complet du plan ou de l'espace.
– a. Tessellation, tiling

Carroll (diagramme de -): représentation des éléments d'un ensemble: ceux qui appartiennent dans une case et les autres dans une autre. Peut être étendu à plusieurs appartenances.
– v. Diagramme de Carroll, diagramme de Karnaugh, paradoxe de Lewis Carroll
– a. Carroll diagram: a diagram used for grouping things in a yes/no fashion

Cartésien: caractérise ce qui repose sur la représentation des points du plan par un couple de nombres (x et y).
Ce qui est appelé le système de coordonnées cartésien ou repère cartésien.
Système original dû à René Descartes (1637).
– v. Cartésien
– a. Cartesian

Cartésien (système de coordonnées – ou repère – ou graphique -): système d'axes à deux ou trois axes.
Graphique dont les axes rectilignes se croisent au point d’origine des coordonnées.
– ex. Graphique ou repère, cartésien orthogonal (axes perpendiculaires) et orthonormé (mêmes unités de longueur sur les axes) – Illustration.
– v. Repère
– a. Cartesian coordinate system, rectangulat coordinates

Produit cartésien de l'ensemble E par l'ensemble F: ensemble de tous les couples associant un élément de l'un à un élément de l'autre.
Sorte de résumé d'une table de multiplications non exécutées. Voir illustration.
– symb. A ☓ B se lit A produit cartésien B. (Unicode: 2613).
– ex. E = {1, 2, 3} et F = {A, B, C} :
A ☓ B = {(1,A), (2,A), (3,A), (1,B), (2,B), (3,B), (1,C), (2,C), (3,C)}
– v. Produit cartésien
– Carré cartésien: produit cartésien d'un ensemble sur lui-même.
– a. Cartesian product

Équation cartésienne: d'une manière générale, une équation cartésienne dans le plan s'écrit: f(x) = 0. La fonction f(x) peut être représentée par une courbe f(x, y) = 0 dans un système de coordonnées cartésien.
– ex. équation d'une droite: ax + by + c = 0. Équation du cercle de rayon 1, cad. tous les points à la distance 1 de l'origine: x² + y² - 1 = 0.
– a. Cartesian equation of a line, of a circle. An equation of a curve or surface in which the variables are the cartesian coordinates of a point on the curve or surface.

Catalan (nombres de -)* nombres utilisés en combinatoire. Très nombreuses applications.

Les premiers sont: 1, 1, 2, 5, 14, 42, 132 …
– v. Nombres de Catalan
– a. Catalan numbers

Cathètes: côtés du triangle rectangle par opposition à l'hypoténuse.
– a. Cathetus: either of the sides that are adjacent to the right angle.

Cauchy (suite de -)**: suite de réels, de complexes, de points d'un espace métrique ou plus généralement d'un espace uniforme, dont les termes se rapprochent les uns des autres. Ces suites sont celles susceptibles de converger. Elles sont au centre de la définition de la complétude.
– v. Suite de Cauchy, espace complet
– a. Cauchy sequence

Cavalière (perspective -): projection (représentation) en 2D d'objets 3D, sans effet de fuite.
– v. Perspective
– a. Oblique projection

Caveat: exprime une réserve, un avertissement préliminaire.
– étym. du latin: caveat: il doit faire attention.

Cayley (table de -): sorte de table de "multiplication" (tableau à double entrée) utilisées pour définir une loi de composition interne (une opération) sur un groupe fini.
Sa lecture est riche d'enseignement: étude des propriétés du groupe fini qu'elle représente.
– origine: Arthur Cayley en 1854
– v. Table de Cayley, carré latin
– a. Cayley table

Graphe de Cayley*: représentation de la table par un graphe dès que la quantité de variables grandit. Cette représentation permet de repérer la structure interne du groupe: identification de générateurs, de sous-groupes qui via la même loi vont redonner tous les éléments du groupe.
– a. Cayley graph

Cc: cubic centimeter.
Abréviation en anglais (pas en français) de l'unité de volume: centimètre cube (cm³).

Célérité: synonyme de vitesse pour une onde; sa vitesse de propagation;
– ex. Célérité de la lumière
– a. Celerity

Cellule d'un polytope: un polyèdre (3D) possède des arêtes et des faces. Un polytope (>3D) possèdent en plus des cellules
– a. Edgse, faces and facets

Cent = 100 = 10²
– Orthographe: deux cents, mais deux cent vingt.
– v. Cent, le nombre 100 et culture
– a. Hundred

Centaine: quantité voisine de cent.
– a. Hundred; plus d'une centaine de fois: over one hundred times
Centième: vaut 1/100.
– a. Hundredth; the hundreth anniversary
Centuple: multiplié par cent.
– a. Hundredfold;

Centile: partage une population en cent parties de même effectif.
– ex. le quatre-vingt-quinzième centile (ou nonante-cinquième centile) est la valeur telle que 95 % des valeurs mesurées sont en dessous et 5 % sont au-dessus.
– v. Quartile, quantile, pourcentile
– a. Percentile

Centrale (symétrie -): l'image M' d'un point M est son symétrique par rapport à un point O, le centre de symétrie.
C'est une transformation affine, une involution.
– ex. le 9 est l'image du 6 par symétrie centrale (Illustration)
– v. Symétrie
– a. Point reflection, central inversion

Centre: point milieu d'une figure.
Point d’un objet à une égale distance de l’ensemble des éléments de cet objet.
– ex. centre du cercle, de la sphère, du polygone régulier, d'un segment, d'un arc, …

Centre du cercle: point à égale distance de tous les points du cercle.
– v. Cercle, vocabulaire du cercle, construction du cercle sans connaitre le centre
– a. Central point

Centre de gravité: point d'équilibre d'un objet.
Dans un triangle, c'est le point de concours des médianes.
– v. Centre de gravité, barycentre, isobarycentre
– v. Centre de gravité, calcul du centre de gravité
– a. Gravity center, center of mass, centroïd

Centre de symétrie: tous les points de la figure sont deux à deux symétriques par rapport à ce centre; point par rapport auquel la figure est invariante par une symétrie centrale.
– v. Symétrie
Symmetry center

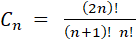
Centre d'une homothétie: point de rencontre des lignes de tracé de l'homothétie (Illustration)
– v. Similitude
– a. Homothetic center

Anticentre: point symétrique du centre par rapport à un point situé sur le cercle ou la sphère.
Utilisé en astronomie: l'anticentre de notre Galaxie est le point symétrique du centre de la Galaxie par rapport au Soleil.
– a. Galactic anticenter

Centrée réduite (variable aléatoire - )* en gros sa moyenne est nulle. Utile pour effectuer des comparaisons.
Une variable centrée réduite à une espérance nulle, une variance égale à 1 et un écart type égal à 1. Ainsi, on obtient des données indépendantes de l’unité ou de l’échelle choisie, des variables ayant même moyenne et même dispersion.
– v. Réduite
– a. Centered variable, standardized variable

Centered independent variables are obtained just by subtracting the mean of the variable. Standardized variables are obtained by subtracting the mean of the variable and by dividing by the standard deviation of that same variable.

Centrosymétrique: Un polygone est dit centrosymétrique quand il présente un centre de symétrie.
– a. Centrosymmetry

Cercle: figure géométrique plane dont tous les points sont à égales distance du centre; des points sur le même cercle sont dits cocycliques; mot qui vient du latin circulus, un diminutif de cirque
– v. Cercle, vocabulaire du cercle
– a. Circle

Cercles inscrit, exinscrits, circonscrit: Voir Cercle circonscrit, cercle inscrit …
– a. Incircle, excircle, cicumcircle

Cercles concentriques: Voir Cercles concentriques
– a. Incircle, excircle, cicumcircle

Grand cercle: sur une sphère cercle dont le plan passe par le centre de la sphère
– v. Géodésique, arc de grand cercle, triangle sphérique.
– v. Sphère terrestre.
– a. Great cicle or orthodrome

Cercle et droite: une droite est soit extérieure au cercle, soit tangente au cercle, soit sécante au cercle.

Cercle et cercle: des cercles de même centre sont dits concentriques; deux cercles qui se coupent en deux points sont dits sécants; deux cercles qui ont un seul point commun sont dits tangents.

Cercles et triangle:
– v . Cercle et triangles: circonscrit, inscrit, exinscrits

Cercle trigonométrique: cercle de rayon unité et orienté positif dans le sens antihoraire.
– v. Cercle trigonométrique
– a. Unit circle; clockwise and counterclockwise (É-U) or anticlockwise (RU).

Cercle déférent: cercle sur lequel, selon les Anciens, se déplacent les planètes.
Les planètes tournent sur un épicycle qui lui-même tourne sur un déférent.
– v. Mouvement rétrograde
– a. Deferent and epicycle

Cerf-volant (ou pseudo-carré): quadrilatère ayant deux paires de côtés adjacents égaux.
– v. Famille des quadrilatères
– a. Kite: a quadrilateral with two pairs of adjacent sides that are the same length.

Certain (événement): dont la probabilité d'occurrence est sûre, soit égale à 1.
L'univers Ω, regroupant toutes les issues possibles, est un événement certain.
Contraire de: improbable ou impossible.
Ne pas confondre avec affirmation vraie.
– v. Probabilités et statistiques
– a. the event is certain, impossible or probable

Cévienne: droite passant par le sommet d'un triangle comme la bissectrice, la hauteur ou la médiane (la médiatrice n'est pas une cévienne).
– v. Céviennes / Théorème de Ceva / Ménélienne
– a. Cevian

Chaîne de divisibilité: Suite indicée de nombres telle que: un élément de rang n est divisible par un de rang m si n est divisible par m.
– ex. Les multiples de n.
– v. Divisibilité
– a. Divisibility chain

Chaîne d'opérations: suite de calculs à réaliser avec nombre, symboles et parenthèses.
– v. Calcul, priorité des opérations, calcul algébrique, expression
– a. Expression or mathematical expression

Chaînette: courbe caractérisée par l'emploi d'exponentielles.
– v. Chaînette
– a. Catenary

Champ*: étendue d'espace dans laquelle une force a un effet sur la matière. Un aimant exerce une action partout autour de lui, mais avec une intensité et un sens qui évolue avec la position; à chaque point on peut y associer un vecteur; le champ est l'ensemble de tous les vecteurs; ex: le champ magnétique ou le champ électrique; le champ peut être un caractérisé par un vecteur (comme indiqué ci-avant) ou un simple nombre (scalaire), ou un super vecteur (tenseur).
– v. Champ, champ électromagnétique
– v. Champs en mathématiques: scalaire, spinoriel, vectoriel, tensoriel.
– a. Field, electromagnetic field

Chaos (théorie du -)* certains phénomènes, même modélisés par des équations parfois simples, semblent complètement erratiques; ils font partie de cette nouvelle branche des mathématiques.
Étude du comportement de systèmes très sensibles aux conditions initiales.
Domaine des systèmes dynamiques.
Effet papillon.
– v. Chaos, théorie du chaos, attracteur, fractale, complexité, variété
– a. Chaos theory, butterfly effect

Chasles (relation de-): relation relative à une somme de vecteurs:

remarquez l'enchaînement des lettres
– v. Vecteur, exemple d'application, inégalité triangulaire
– a. Segment addition postulate

Étant donnés deux points A et C, un troisième point C est situé sur le segment AC, si et seulement si la relation AB + BC = AC est satisfaite.

Chat-GPT: generative pre-trained transformer. Une intelligence artificielle formée à base de plusieurs couches de neurones informatiques et utilisant l'apprentissage par renforcement guidé par l'humain.
Chat-GP-3, mis en service en 2023, compte 175 milliards de paramètres et a été entrainé à partir de 570 Go de textes.
– v. IA, Réseaux de neurones, Machine learning & Deep learning
– a. Artificial intelligence

La modélisation d'un texte passe par la vectorisation. Un texte est vu comme une suite de mots, et chaque suite de mots est représentée par un vecteur dans l'espace de tout le vocabulaire utilisable. L'algorithme GPT consiste à prédire le mot n+1 connaissant les mots de 1 à n.

Chemin: sur un graphe, enchainement de liens.
Suite finie d'arcs consécutifs dans un graphe orienté.
Un chemin relie un point initial à un point final.
– voisin: si le graphe n'est pas orienté, il s'agit d'une chaine.
– v. Chemin eulérien: tracé en un seul trait, topologie
– a. Path, path graph

Lacet: chemin fermé.
– a. Loop (littéralement: boucle).

Chemin sur réseau: ligne brisée prenant appui sur les points d'un quadrillage régulier (réseau).
Un tel chemin est définit par une suite de couple de coordonnées.
La quantité de chemins pour rejoindre un point de coordonnées (a, b) est le coefficient binomial .
– v. Chemins sur réseau
– a. Lattice paths: a path composed of connected horizontal and vertical line segments, each passing between adjacent lattice points.

Chemin auto-évitant: chemin sur réseau qui ne repasse jamais sur le même point.
– v. Chemins auto-évitant
– a. Self-avoiding walk: a path from one point to another which never intersects itself.

Graphe chemin: arbre où chaque nœud est de degré deux, au plus.

Graphe eulérien: un chemin qui passe par toutes les arêtes exactement une fois.
– v. Graphe eulérien
– a. Eulerian path: a walk that uses every edge of a graph exactly once.

Graphe hamiltonien: graphe qui a au moins un cycle passant par tous les sommets exactement une fois, et ce cycle est appelé cycle hamiltonien
– v. Graphe hamiltonien
– a. Hamiltonian path or cycle:

Chien (courbe du – ou courbe de poursuite)* le maître avance régulièrement, le chien le rejoint en adaptant la direction de sa course; Sa trajectoire est la courbe du chien.
– a. Pursuit curve

Chiffre: chacun des symboles permettant d'écrire les nombres.
En numération décimale les chiffres sont 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.
En hexadécimal on ajoute A, B, C,D, E et F.
En binaire ce sont simplement 0 et 1.
– étym. Le mot chiffre vient curieusement de l'arabe sifr qui veut dire zéro, vide; en italien il est devenu cifra (tchifra)
Il existe plusieurs manières d'écrire le même nombre: 1,5 = 1 ½ = 15/10 = 3/2 …
– v. Histoire des chiffres, Écriture des chiffres
– a. Digit, numeral
Numeral: a symbol that is not a word and represents a number, such as the Hindu-Arabic numerals: 1, 2, 3, …

Chiffres romains: Les différents symboles servant compter en Romain: I, V, X, L, D et M.
La numération romaine est un système de numération additive
– v. Chiffres romains
– a. Roman numerals

Chiffres arabes: Nos chiffres sont dits "arabes" ou plutôt "indo-arabes", alors que les arabes n'utilisent pas nos chiffres. (Illustration)
– v. Histoire des chiffres, Écriture des chiffres
– a. Arabic numeral

Chiffre certain: Voir Chiffres significatifs

Chiffrement ou cryptage: comment écrire des messages secrets avec des chiffre; généralisation à toute méthode pour obtenir un message secret.
– ex. Un algorithme qui permet de chiffrer des données.
– v. Cryptographie
– a. Encryption, encoding information

Chinois (théorème -): solution à un type de problème impliquant des restes de division (des congruences)
– v. Théorème des restes chinois avec des exemples
– a. Chinese remainder theorem

Chisanbot: opérations réalisées avec les doigts façon boulier.
– v. Calcul mental avec les doigts
– a. Finger mental maths, chisanbot

CHP***: calcul haute performance.
– v. Ordinateurs et superordinateurs
– a. HPC: high performance computation.

Le calcul haute performance consiste à associer un grand nombre de processeurs – de plusieurs milliers à plusieurs millions – pour construire des architectures de calcul en parallèle et diminuer les temps de calcul.
Applications: modélisation des évolutions du climat, optimisation de la production d’énergie, analyse des sous-sols pour la recherche de pétrole, simulation technologique, craquage des codes en cryptographie, analyse financière, etc.

Chromatique (nombre -): quantité maximale de couleurs nécessaire pour colorier un graphe sans que deux sommets adjacents aient la même couleur.
– v. Nombre chromatique, théorème des quatre couleurs, graphe coloré
– a. Chromatic number: The smallest number of colors needed to color a graph.

Cinématique: étude du mouvement de points dans un repère.
– a. Kinematics

Cinq: 5
– v. Nombre 5
– a. Five

Circonférence: ligne courbe, périmètre du cercle dont la longueur vaut
– v. Cercle, constante Pi

Circonscrit (cercle -): cercle qui passe par tous les sommets du polygone.
Le centre du cercle circonscrit à un triangle est le point de concours des trois médiatrices du triangle; c'est le milieu de l'hypoténuse pour un triangle rectangle.
– v. Cercle circonscrit, cercle et triangle
– a. Circumscribed circle or circumcircle: a circle which passes through all three vertices of a triangle

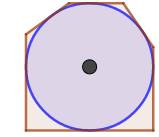
Circonscrit (polygone -): polygone dont les côtés sont tous tangents à un cercle. Illustration
– a. Circumscribed polygon

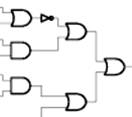Circuit logique: fonction logique représentée un schéma comportant des portes logiques.
– v. Opérateusr logiques, addition, automate
– v. Logic circuits, networlks

Curiosité: un circuit logique comporte d'un côté des entrées et de l'autre des sorties. Il n'est donc pas fermé comme le voudrait l'étymologie du mot (circulus, circueo: aller autour).

Circulaire (fonction -): les fonctions trigonométrique s'appuyant sur le cercle trigonométrique: sinus, cosinus, tangente, cotangente, sécante et cosécante
– v. Trigonométrie
– a. Trigonometric functions or circular functions

Circonscriptible (ou tangentiel): polygone dont tous les côtés sont tangents à un même cercle. Anglais: tangential polygon or circumscribed polygon.
– v. illustration /
– v. Cercle circonscrit

Cis: fonction trigonométrique complexe valant cos x + i sin x = .

Classe: sous-ensemble défini par une relation d'équivalence;
En bref: une famille de nombres partageant la même propriété comme la classe des nombres pairs.
– syn. Ensemble
– v. Classe
– a. Class (set theory): a class is a collection of sets

Classe de restes modulo n: ensemble des nombres d'un ensemble qui ont le même reste par la division par n.
– ex. E = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} avec la division par 4, on aura {4, 8} avec reste 0; {1, 5, 9} avec reste 1; {2, 6, 10} avec reste 2; et {3, 7} pour le reste 3. Soit quatre classes d'équivalence.
– v. Relation d'équivalence
– a. Equivalence class

Classe de valeurs: en statistique, regroupement par même valeur d'un caractère.
– ex. La classe de tous les usagers ayant pris le train entre 8h et 9h.
– v. Classe: Each equivalence relation provides a partition of the underlying set into disjoint equivalence classes.

Classes (théorie des -)** dans ce cas classe est proche d'ensemble; la différence tient au fait qu'un ensemble peut-être lui-même un ensemble, ce qui n'est pas le cas pour une classe; cette subtile différence permet d'éviter certains paradoxes comme celui de Russell.

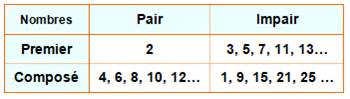
Classe d'équivalence: Si on prend l'ensemble des nombres entiers (N), la relation R = "divisible par 2" séparent les nombres pairs des nombres impairs.
L'ensemble des nombres est partitionné (partagé) en deux classes d'équivalence: le sous-ensemble des nombres pairs (P) et le sous-ensemble des nombres impairs (I).
L'ensemble ainsi partitionné par R, donc constitué de deux sous-ensembles, est l'ensemble quotient de N par R.
– v. Relation d'équivalence, congruences
– a. Coset

Classe d'équivalence avec les diviseurs
– v. Classe des diviseurs de 12

Classification décimale universelle (CDU): numérotation des connaissances par rubriques numérotées.
– ex. 5: Sciences exactes; 51: Mathématiques; 511: Théorie des nombres
– v. Classification universelle
– a. Universal Decimal Classification (UDC)

Classification supervisée ou non: en informatique (machine learning), méthodes de classement utilisant des rubriques connues pour les cas "supervisés " (comme la classification des animaux). Dans le cas "non supervisé", l'algorithme essaie de découvrir la structure interne des données.
– a. Clustering (non supervisé) et classification (supervisé)

Clé de cryptage* information permettant de décoder un message secret en cryptographie; souvent un nombre composé, produit de facteurs premiers de très grande taille de sorte ue le nombre composé connu, il est quasiment impossible avec la technologie actuelle de retrouver les facteurs
Clé publique: clé connue de tous, mais qui ne peut être exploitée par des tiers; ex: système de cryptage RSA
– v. Cryptographie RSA

Clique d'un graphe: sous-ensemble des sommets d'un graphe dont le sous-graphe induit est complet, c'est-à-dire que deux sommets quelconques de la clique sont toujours adjacents.
Généralisation à une structure donnée dans un ensemble. La théorie de Ramsey dit qu'une telle structure moochromatqiue est inévitable pour un ensemble suffisamment grand.
Le nombre-clique est la taille de la plus grande clique.
– v. Vocabulaire des graphes
– a. Clique (graph theory), clique number

CNS: condition nécessaire et suffisante.
– v. Équivalence

Cloche (courbe en -)*: courbe de Gauss, représentative de nombreux phénomènes de hasard.
– fonction: loi normale
– v. Courbe en cloche, Gauss

Clos (ensemble algébriquement -)** généralisation de la notion d'ensemble fermé ou stable.
Soit un ensemble G non stable par une relation . S'il existe un ensemble F de E tel que G est inclus dans F et que F est stable pour , alors F est la clôture ou la fermeture de G dans E.
Ex: L’ensemble des rationnels est clos pour l’addition et la multiplication et leurs opérations réciproques (soustraction et division).
– v. Ensemble clos et ensemble ouvert
– a. Closed set and open set

Le polynôme x² + 1 = 0 n’a pas de racines dans l’ensemble ℝ des nombres réels ? Mais, il a deux racines complexes : + i et - i. Il existe donc des polynômes à coefficients réels n’ayant pas de racines réelles. Mais, tout polynôme à coefficients réels ou complexes a des racines complexes. On dit que le corps C (ensemble des nombres complexes) est algébriquement clos.

C_n^p Notation d'une quantité qui revient souvent dans les questions de dénombrement;
; C'est le nombre de combinaisons de n objets pris p à p; c'est le coefficient du binôme de Newton; ces valeurs sont aussi présentes dans le triangle de Pascal.
– v. Coefficients du binôme

CNS: Condition nécessaire et suffisante.
– a. necessity and sufficiency, necessary and sufficient condition

Coaxial: objets qui partagent le même axe.
– ex. Cylindres coaxiaux; câbles coaxiaux.
– a. Coaxial, coaxal

Cocycliques (points -): points appartenant tous au même cercle.
Deux points ou trois points non alignés sont toujours cocycliques.
– v. Cocyclique, concentriques, puissance d'un point, théorème de Ptolémée, quadrilatère et réflexions
– a. Concyclic or cocyclic

Code: système de lettres, chiffres ou symboles servant à communiquer un message.
Le code: langage de programmation qui sert à créer des logiciels (des programmes informatiques).
Code binaire: code (ou programme) en langage binaire, indispensable pour communiquer avec le matériel de l'ordinateur.
– v. Liste des programmes sur ce site >>>

Coder: transformer un message pour le traiter, le compacter (compresser), le transmettre, le rendre incompréhensible aux tiers, indéchiffrable
– v. Chiffrement RSA, cryptologie

Coder en informatique: créer, rédiger un programme.
Un programme écrit doit être testé et débogué (corrigé, déverminé).
– syn. programmer, écrire du logiciel
– v. Débogage, recette, Scratch, Python, Maple, Maxima
– a. Coding, writing instructions, writing a computer program; testing, debugging

Coefficient: nombre multiplicatif dans une expression algébrique.
– ex. Pour le polynôme 3x² – 4x + 10, les coefficients sont: 3, -4 et 10.
– v. Paramètre, scalaire
– a. Coefficient, the highest degree of the variable in a polynomial is referred to as the leading coefficient.

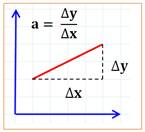
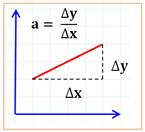
Coefficient directeur: valeur du coefficient a dans l'équation de la droite y = ax + b.
Témoigne de la pente de la droite (Illustration).
Le coefficient peut être positif (montée), nul (plat) ou négatif (descente).
La droite verticale a une pente indéfinie (division pas zéro impossible).
– a. Slope of a straight line, gradient; to calculate the slope, divide the change in height by the change in horizontal distance. A vertical line's slope is udefined.

Dans un repère Ox, Oy l’équation d’une droite non parallèle à Oy est de la forme : y = ax + b, où a et b sont deux nombres réels. Le nombre a est appelé coefficient directeur de la droite. Si le repère Ox, Oy est orthonormé ce coefficient directeur est encore appelé pente de la droite.

Coefficient de proportionnalité: facteur par lequel il faut multiplier tous les nombres d'un ensemble (d'une suite de nombres) pour obtenir tous les autres.
– ex. Entre {1, 2, 3} et {10, 20, 30} le coefficient de proportionnalité est 10.
– v. Suites proportionnelles, constante de proportionnalité
– a. Coefficient of proportionality: In proportional sequences, the number by which a term in the first sequence has to be multiplied to obtain the term with the same rank in the second sequence. The coefficient of proportionality is equal to the inverse of the constant of proportionality.

Coefficient de pondération: v. Moyenne pondéré
– a. Weighting coefficient or factor, weighted sum method

Coefficient binomial ou coefficient du binôme: Voir en Coefficients du binôme
– a. Binomial coefficient

Cœur (par -): de mémoire, sans recours à autre chose que sa tête.
Connaitre par cœur: savoir complètement, à fond, sans se tromper.
– a. Rote: I can rote counting from 0 to 20 (Je peux compter par cœur de 0 à 20).

Cohomologie: d'une manière générale, la cohomologie mesure dans quelle mesure les choses qui peuvent être faites localement ne peuvent pas être faites à grande échelle. Exemple: le tribar (illustration): on peut réaliser physiquement un morceau par l'objet entier quelle que soit la colle ou la soudure utilisée.
La cohomologie est un invariant de l'espace topologique, formellement dual de l'homologie. Elle détecte des 'trous" dans l'espace. Elle a une structure algébrique plus importante que l'homologie.
– a. Cohomologie

Col (point-col ou point-selle): qui est minimum selon un axe et maximum selon un autre
Point de passage au col (flèche rouge) sur cet exemple de paraboloïde hyperbolique.
– a. Saddle point

Colinéaires (points -): qui appartiennent à un même droite.
– syn. Alignés
– v. Colinéaire et coplanaire, diamétralement opposés.
– a. colinear points: collinear points are points that lie on the straight line.

Colinéaires (vecteurs -): qui appartiennent à la même droite ou à des droites parallèles; ce sont des vecteurs qui ont même direction.
– v. Colinéaire et coplanaire
– a. Collinear vectors: they are parallel to the same given line.

Collection: mot générique pour indiquer un regroupement d'objets similaires au sens classique et intuitif de chacun.
Une collection d'objets mathématiques est un ensemble.
On ne peut pas utiliser le mot groupe qui est un ensemble très particulier.
– a. Collection

Colonne: rangée verticale dans un tableau, un carré magique, une matrice …
– v. Ligne
– a. Column: an arrangement of figures, one above the other.

Combinaison: tout choix de p éléments parmi n.
L'ordre est sans importante. Lorsque c'est le cas, on parle d'arrangement.
La quantité de combinaisons sans répétition est égale à C_n^p .
– v. Combinaison
– a. Combination: any of the ways we can combine things, when the order does not matter. When the order does matter, it is a permutation.

Combinaison linéaire de deux (ou n) grandeurs: somme pondérée par des coefficients de chacune des grandeurs.
Combinaison linéaire de a et b: u.a + b.v.
Les grandeurs peuvent être des objets mathématiques comme des vecteurs.
Les coefficients restant des nombres (scalaires).

Combinatoire (analyse -): partie des mathématiques consacrée à l'art de compter, de dénombrer; branche des mathématiques qui étudie les combinaisons, les dénombrements ou les configurations d'ensembles finis;
– v. Combinatoire, vocabulaire du dénombrement"
– a. Combinatorics: a branch of mathematics which is about counting.

C’est étudier comment se comporte une suite de nombres, ou d’objets, qui ont un début et une fin", explique Guillaume Chapuy, "combinatoriste",

Commensurable: se dit de deux grandeurs dans un rapport rationnel, que l'on peut évaluer avec la même unité.
Dans le cas contraire, elles sont incommensurables et le rapport est un nombre irrationnel (un nombre à décimales sans fin et sans répétition).
Deux nombres a et b sont commensurables si la fraction a/b est rationnelle.
– étym. Du latin cum mensura, mesure commune.
– v. Aliquote
– a. Commensurable; ne pas confondre avec commensurate (he was given a job commensurate with his abilities)

Commensurable: En anglais, se traduit parfois par divisible.
Divisible without remainder by a common unit.
– a. The number 42 is commensurable by 6 and 7.

Commun (facteur -): a (c+d) + b (c+d) mis en facteur commun donne (a +b) (c+d).
– v. Techniques de base de l'algèbre, mots usuels du calcul

Commutativité (commutatif): l'ordre des termes ne change pas le résultat; 1 + 2 + 3 = 3 + 2 + 1; l'addition et la multiplication sont commutatives; la soustraction et la division ne le sont pas.
– v. Groupe, abélien ou commutatif, distributivité, associativité, vocabulaire des structures algébriques

La loi de composition interne, notée *, définie sur l’ensemble E, est commutative si, quel que soit le couple (a, b) d’éléments de E, le composé de a avec b et le composé de b avec a sont deux éléments égaux :

Quels que soient les éléments a et b de E, a étoile b est égal à b étoile a.

Addition et multiplication sont commutatives, mais pas la soustraction.

Groupe commutatif ou abélien: si un ensemble E a structure de groupe pour la loi de composition interne *, on dit que ce groupe est commutatif si la loi * est commutative (on dit aussi qu’il est abélien).

Anneau ou corps commutatif: si un ensemble E muni de deux lois de composition interne (notées + et x) a une structure d’anneau (ou de corps), on dit que c’est un anneau (ou un corps) commutatif si la loi notée x est commutative (la loi notée + est toujours commutative).

Compact**: Un espace topologique E est dit compact s'il est séparé et si tout recouvrement ouvert de E contient un sous-recouvrement fini.
– ex. Deux points distincts A et B sur une droite. Si l'ensemble formé par ces deux points peut-être recouvert par des intervalles, alors l'un des intervalles contient A et un autre (peut-être le même) contient B. Il suffit donc d'au moins deux intervalles pour recouvrir notre ensemble: il est compact.
Le théorème de Bolzano-Weierstrass dit essentiellement qu'un segment [a, n] de est compact.
– a. Compact space, compactness

Un espace topologique E est compact s’il satisfait aux deux propriétés suivantes :

il est séparé; et

on peut extraire un recouvrement fini de tout recouvrement ouvert de E.

Les intervalles fermés bornés [a, b] de R sont des ensembles compacts, car :

1) [a, b] est séparé ; quels que soient les points distincts x et y de cet intervalle, on peut toujours trouver un voisinage de x et un voisinage de y qui ne se rencontrent pas ;

2) De tout recouvrement ouvert de [a, b], on peut extraire un recouvrement fini (la démonstration existe).

ℝ n’est pas compact. La droite numérique achevée ℝ est compacte.

Compas: instrument qui permet de dessiner des cercles
– v. Construction à la règle et au compas
– a. Compass (drawing tool), compasses-and-straightedge constructions: these constructions use only compass, straightedge (i.e. ruler) and a pencil.

Comparable: si E est un ensemble muni d’une relation d’ordre notée ≤ , deux éléments x et y de E sont comparables si l’une au moins des deux propositions x est inférieur à y ou y est inférieur à x est vraie.
Dans le cas d’une relation d’ordre total, deux éléments quelconques de E sont toujours comparables; dans le cas d’une relation d’ordre partiel, il existe des couples d’éléments de E non comparables.

Comparaison de deux nombres: c'est dire lequel est le plus petit ou le plus grand des deux nombres.
– ex. Entre 0,1234 et 0,12339 le premier est le plus grand;
       entre 2³ et 3² le second est le plus grand;
       entre racine de 10 et 10/3 le second est le plus grand (3,16 et 3,33);
       entre 5/7 et 3/4 le second est le plus grand (20/28 et 21/28).
– v. Égal, inférieur, différent, supérieur, inégalité
– a. Comparing numbers

Compatible: si E est un ensemble sur lequel sont définies une relation d’équivalence et une loi de composition interne notée *, on dit que est compatible avec la loi * si, lorsque x est équivalent à x’ et y à y’, alors le composé x * y est équivalent au composé x’ * y’.

– ex. Soit l'ensemble ℤ et la relation définie par x a même reste dans la division par 2 que y. Cette relation d’équivalence est compatible avec l’addition, car, si x a même reste que x’ et y même reste que y’ dans la division par 2, x + y a même reste que x’ + y’ dans la division par 2.
– a. Compatible

Compilateur: en informatique, programme de traduction d'un langage en un autre, habituellement d'un langage proche de l'humain (dit langage évolué) vers un langage plus proche de la machine matérielle, et cela en cascade jusqu'au codage ultime des instructions en binaire.
– a. Compiler

Complément: le complément à m de n est le nombre qu'il faut ajouter à n pour obtenir m.
Le complément à 10 de 7 est égal à 3 (pour certains: 8 + 5 = (8+2) + 3 = 13.
Notion très utile pour le calcul mental.
– v. Théorème de Midy ou de la demi-somme des périodes
– a. Complement, the tens complement is the number we add to make 10.

Complément (logique): C'est le nombre binaire obtenu en inversant chaque bit.
La fonction OU entre le nombre et son complément est égale à un nombre binaire fait de "1".
– a. Logical complement, the 1's complement (101 becomes 010), the 2's complement add "1" (101 becomes 010 + 1 = 011)

Complémentaires (angles -): dont la somme vaut 90°, soit / 2 = 1, 57 … radian.
Ils forment un angle droit (Illustration)
Ils ne sont pas forcément voisins; pourvu que la somme soit 90°.
Dans un triangle rectangles des deux angles non-droits sont complémentaires.
– v. Supplémentaire
– a. Complementary angles: Two angles are complementary when they add up to 90 degrees (a right angle).

Complémentaires (ensembles -): ensembles dont la réunion forme l'ensemble total.
Tous les éléments de l'univers qui ne sont pas dans l'ensemble considéré.
– ex. Aux dés: A' = {4, 5, 6} est le complément de a = {1, 2, 3}. Notation avec un prime.
– a. Complement of a set

Complémentaires (événements): événements disjoints dont la somme des probabilités est 1.
Toutes les issues qui ne sont pas l'événement considéré.
– ex. À pile ou face, l'événement complémentaire de pile est face et inversement.
– ex. Aux dés: A' = {4, 5, 6} est l'événement complémentaire de a = {1, 2, 3}. Notation avec un prime.
– a. Complement of an event

Complémentaires (couleurs): couple de couleurs qui, mélangées, annulent la perception de couleur, produisant un gris neutre.
– a. Complementary colors

Complémentaire (triangle -): triangle dont les sommets sont les points milieux des côtés d'un triangle donné; les deux triangles sont homothétiques.
– v. Triangle médian
– a. Midpoint triangle or medial triangle

Complémentation: en logique, prendre la négation d'une proposition.
– Notation:
– v. Complément, négation, réunion, intersection
– a. To negate a proposition

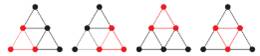
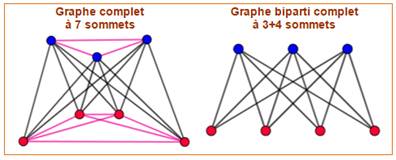
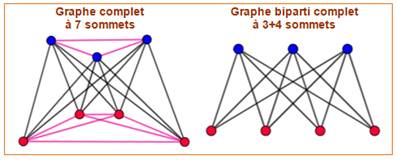Complet:
Graphe complet ou polygone complet: graphe ou polygone muni de toutes les arêtes ou diagonales.
– v. Graphe complet, nombres de Ramsey (coloration des graphes complets)
– a. Complete graph

Graphe biparti complet: chaque sommet du premier ensemble est relié à tous les sommets du second ensemble.
– v. Graphe biparti complet,
– a. Complete bipartite graph

Jeu à information complète: jeu où le hasard est exclu comme aux échecs ou au jeu de GO.
Jeux de stratégie combinatoire abstraits (abstrait car ne fait référence à rien dans le monde réel, contrairement aux jeux de simulation, par exemple).
– a. Game with complete information: the knowledge about other players is available to all participants

Espace complet**: espace qui n'a pas de trou, aucun point manquant.
Avec la notion usuelle de la distance, l'espace des nombres réels est complet, mais pas celui des nombres rationnels.
Un espace complet est un espace métrique dans lequel toute suite de Cauchy est convergente.
– v. Espace de Hilbert

Complexe (nombre -): nombre (z) composé dune partie réelle (a) et d'une partie imaginaire (b) introduite par le symbole i, soit z = a + ib.
a est la partei réelle, b la partie imaginaire et i l'unité imaginaire
Sa forme polaire est z = r (cos q + i sin q) avec r le module et q l'argument.
Ils forment l'ensemble noté .
– propriétés: .
– v. Nombre complexe – Index , vocabulaire des nombres complexes, imaginaire, quaternion
– a. Complex number: a combination of a real number and an imaginary number, real part, imaginary part, imaginary unit

Complexité d'un objet* comment caractériser la difficulté d'appréhender un objet mathématique? Deux pistes: donner la taille du plus petit algorithme permettant de décrire l'objet; déterminer le temps de calcul de l'algorithme minimal décrivant l'objet
– v. Complexité, fractale, chaos.
– a. Complexity

Componendo et dividendo: Méthode de simplification de fractions.
– v. Componendo et dividendo

Composante: dans un couple (x, y), l’élément x est appelé première composante du couple et l’élément y deuxième composante.
– a. Component

Composantes d'un vecteur: les coordonnées de ce vecteur: norme, direction et sens.
– v. Vecteurs
– a. Vector component x and y.

Composé (nombre -): nombre qui peut se mettre sous a forme d'une multiplication de deux nombres; nombre non-premier; ex: 4 = 2 x 2, 20 = 2 x 2 x 5, 100 = 4 x 25 = 2 x 2 x 5 x 5 = 2² x 5² .
– v. Nombre composé
– a. Composite number: a positive integer that can be formed by multiplying two smaller positive integers.

Composée d'une application: résultat de cette application, notamment d'une loi de composition interne.
– ex. Si le composé x*y appartient à l'ensemble de départ, l'ensemble est fermé.
– v. Vocabulaire des structures algébriques
– a. Map (function) refers to the action of applying a function to the elements of its domain

Le résultat de l’addition de deux nombres entiers x et y est appelé somme de ces deux nombres et noté x + y; le résultat de la multiplication de l’entier x par l’entier y est appelé produit de ces deux nombres et noté x × y ou xy.

De façon générale, si un ensemble E est muni d’une loi de composition interne, dont le symbole est noté * (par exemple), le résultat de la composition de x et de y est appelé le composé des deux éléments x et y et noté x * y.

Composée de transformations: résultat de l'application de plusieurs transformations successives.
– ex. Une symétrie orthogonale puis une autre par rapport à la même droite redonne la figure initiale.
– ex. La composée de deux translations de vecteurs u et v est la translation de vecteur u+v.
La composée de la symétrie de centre A et de la symétrie de centre B est la translation de vecteur 2.AB.
– a. A composite transformation (or composition of transformations) is two or more transformations performed one after the other. Sometimes, a composition of transformations is equivalent to a single transformation.

Règle de dérivation des fonctions composées ou règle de la chaine*: formule explicitant la dérivée d'une fonction composée pour deux fonctions dérivables.
– ex. Une variable y dépend de u et u de x, le taux de variation (la dérivée) de y en fonction de x se calcule selon la formule indiquée.
– a. Chain rule

Composition de fonctions ou d'applications: procédé de construction d'une fonction dite composée, à partir de deux autres.
– notation: g o f. Lue g rond f. Calcul par g( f(x) ).
– attention: la loi de composition n'est pas commutative.
– ex. si f(x) = x + 2 et g(x) = x² alors g o f = (x+2)².
– v. Loi de composition
– a. Function composition: an operation ∘ that takes two functions f and g, and produces a function h = g ∘ f such that h(x) = g(f(x)).

Composition des nombres: toutes les partitions d'un nombre déclinées en tenant compte des permutations des termes. On parle aussi de décompositions ou de partitions induites.
– v. Composition, suite de Narayana
– a. Composition

Compréhension: un ensemble est défini en compréhension s’il est défini à l’aide d’une propriété que possèdent tous ses éléments et qu’ils sont les seuls à posséder.
– ex. La phrase les nombres entiers positifs ou nuls multiples de 3 et plus petits que 20 définit l’ensemble { 0, 3, 6, 9, 12, 15, 18 } en compréhension.
On note aussi :

– contraire: définition par extension en énumérant tous les éléments de l'ensemble
– a. semantic description: a way to define a set by using a rule to determine what the elements are

Compression de données** (ou codage de source): compresser une suite d'information, c'est coder cette information de sorte qu'elle occupe moins de place en mémoire, sans détériorer l'information initiale, ou de manière imperceptible dans le cas des images, par exemple.
– ex. 111123344444455 (15 chiffres) sera comprimé en 4112236425 (10 chiffres) en comptant la quantité de chiffres.
Les techniques de compression sont nombreuses et plus sophistiquées que dans cet exemple simpliste.
– ex. MPest une méthode de compression avec perte d'un signal audio; JPEG est utilisé pour les images.
– v. Entropie de l'information, compression et parcimonie
Data compression, source coding, bit-rate reduction: the process of encoding information using fewer bits than the original representation

Compter: donner le nombre, la quantité d'éléments dans un ensemble
– v. Compter, dénombrer, cardinal, calculer, arithmétique
– a. Calculate, count, reckon

Concaténer (concaténation): assembler, mettre bout à bout pour ne faire qu'un; ex: concaténer 123 et 456 donne 123456.
Une concaténation de 1forme les repunits.
– étym. Latin: cum, ensemble et catena, chaine.
– v. Mot de Fibonacci, exemple de programmation avec concaténation, exemples avec les "doublement carrés" ou encore le jeu des six chiffres pour faire 100.
– a. Concatenate

Concave: synonyme de rentrant, qui présente un creux; pour retenir: idée d'une courbe concave dans un verre, son ventre pend vers le bas, vers la cave, comme la bouche du smiley heureux J
– v. Convexe (antonyme)
– a. Concave and convex

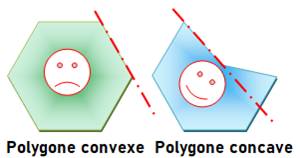
Polygone concave: tel qu'il existe deux points du polygone reliés par un segment non-entièrement contenu dans le polygone. Voir le trait rouge sur l'illustration.
– v. Polygone concave, polygones
– a. Concave polygon

Humour: un cave, en argot, est une personne un peu bête, un peu con. Mais ce n'est pas une personne qu'on vexe facilement.

Concentrique: qui ont même centre.
Concentricité: objets qui partagent le même centre.
– ex. Cercles concentriques, polygones réguliers concentriques
– v. Cercles concentriques, couronne
– a. Concentric objects: sharing the same center point

Concourantes (droites -): droites passant toutes par un même point;.
Droites ayant un point d'intersection, dit point de concours ou point d'intersection ou point de rencontre.
– note: Deux droites sont sécantes; Plus de deux droites peuvent être concourantes en un même point
– v. Théorème de Céva, parallèles, droites remarquables du triangle
– a. Concurrent lines: they intersect at a single point; they are in contrast to parallel lines.

Condensées (mathématiques -)**: théorie développée par Dustin Clausen et Peter Scholze qui vise à unifier divers sous-domaines mathématiques, notamment la topologie, la géométrie complexe et la géométrie algébrique.
– v. Théorie des représentations, programme de Langlands
– a. Condensed mathematics

L'objectif est de créer de nouvelles fondations pour la topologie, en remplaçant la notion traditionnelle d'espace topologique (dont les exemples incluent la sphère et le doughnut) par des objets plus polyvalents qui sont appelés ensembles condensés. Dans cette nouvelle perspective, les espaces topologiques sont pensés comme étant assemblés à partir d'infinis points de poussière collés les uns aux autres, les perfectoïdes.

En 2019, Peter Scholze établit qu'un domaine mathématique appelé analyse fonctionnelle réelle fonctionne toujours si vous remplacez les espaces topologiques par des ensembles condensés. Un théorème majeur des maths pures.

Condition nécessaire et suffisante (abrégé en CNS).
– v. Nécessaire, si et seulement si (ssi)
– a. if and only if (iff).

Condition nécessaire: Pour qu’un nombre entier positif supérieur à 2 est premier s'il est impair (car un nombre pair supérieur à 2 et divisible par 2).

On dit que la condition x est impair différent de 1 est une condition nécessaire pour que x soit premier.

Condition suffisante

La condition x est impair ne suffit pas pour que x soit premier. Par exemple, 15 est impair mais non premier, puisque divisible à la fois par 3 et par 5. Cette condition n’est donc pas suffisante.

En revanche, x étant un nombre entier positif, la condition : la somme des chiffres de x est un multiple de 3 est une condition suffisante pour que x soit divisible par 3, car on a l’implication : Somme des chiffres de x multiple de 3 → x divisible par 3.

Condition nécessaire et suffisante

Si x est divisible par 3, alors la somme de ses chiffres est multiple de 3 et aussi si la somme des chiffres de x est multiple de 3, alors x est divisible par 3. On dit que la condition : la somme des chiffres de x est multiple de 3 est une condition nécessaire et suffisante pour que x soit divisible par 3.

Cône: figure engendrée par une droite (génératrice) passant par un point et s'appuyant sur une courbe fermée (directrice).

Ensemble de droites passant par un même point, appelé sommet du cône, et rencontrant une courbe (C) appelée directrice du cône. Les droites sont appelées génératrices du cône.

Si la courbe (C) est un cercle et si le point S se trouve sur l’axe de ce cercle, le cône est dit cône de révolution. L’axe du cercle est appelé axe du cône.

Cône de révolution: cône classique, celui dont la directrice est un disque et dont le sommet se trouve sur l'axe du disque; solide engendré par la rotation d'un triangle rectangle sur l'un de ses côtés.
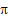– ex. abat-jour ou bille de bois
– étym. Grec: konos, cône, pomme de pin
– v Cône, conique, pyramide.
– a. Cone, cone height formula, slant height of cone, base area of a cone, lateral area of a cone

Cône droit: l'axe est perpendiculaire à la base.
– a. Right circular cone

Cône oblique: l'axe est oblique sur la base.
– a. Oblique cone

Cône tronqué ou tronc de cône: cône étêté par un plan.
– a. Frustum, truncated cone

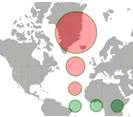Conforme*: transformation (ou application) qui conserve localement les angles.
La projection stéréographique est conforme.
La projection de Mercator l'est également.
L'indicatrice de Tissot (illustration) est un cercle de petite taille à l'équateur et plus grand pour les grandes latitudes.
– v. Géodésique, Loxodromie
– a. Conformal map: a function that locally preserves angles, but not necessarily lengths.

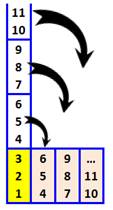Congru, congruence: relation d'équivalence; où il est question de divisions pour lesquelles on s'intéresse uniquement aux restes.
Comme si l'on repliait les nombres pour les mettre dans une cour où seul ce qui dépasse compte:
– ex. 1, 4, 7, 11 sont congrus à 1 dans un repliement par 3, on dit mod 3.
Deux nombres entiers sont dits congrus modulo n si leur différence est un multiple de n, n étant un nombre entier.
On parle d'arithmétique modulaire.
On note N/3N le fait de ramener tous les nombres à leur reste dans la division par 3.
– v. Modulo, nombres congruents, étymologie, portion congrue, relation d'équivalence et ensemble quotient
– a. Congruence: In modular arithmetic, having the same remainder when divided by a specified integer

Congruentes (figures -): figures superposables ("égales").
– Attention: pas forcément isométriques.
– ex. les angles 90° et 270° sont superposables mais non isométriques.
Une acception rigoureuse exige que les figures soient superposables par un déplacement (isométrie directe ou même orientation) et non par symétrie (isométrie indirecte ou orientation inversée).
– v. Égalité et ressemblance en géométrie, transformations du triangle
– a. Congruence: being the same size and shape.

Conique* nom générique des paraboles, hyperboles et ellipses (et le cercle comme ellipse particulière);.
Ces figures résultent de l'intersection d'un cône de révolution par un plan.
– v. Coniques
– a. Conic or conic section: a curve obtained as the intersection of the surface of a cone with a plane.

Conjecture: propriété supposée vraie, mais non encore démontrée.
Tant qu'elle n'est pas démontrée, une conjecture reste une hypothèse.
– ex. Conjecture de Goldbach: tout nombre pair est la somme de deux nombres premiers.
– v. Conjectures; Théorème, axiome, hypothèse, etc.
– a. Conjecture

Conjonction ou produit logique*: connecteur logique noté a Ù b, a ET b ou aussi a · b (algèbre de Boole).
– v. Conjonction, Intersection
– a. Logical conjunction

Conjugué d'un nombre complexe*: nombre complexe qui conserve sa partie réelle, alors que la partie inamgianre est son opposé: a – ib est le conjugué de a + ib.
– notation:
Le produit d'un nombre e t son conjugués donne un nombre réel.
– ex. (3 - 2i) (3 + 2i) = 9 – 4(i²) = 9 + 4 = 13
Une astuce qui consiste à rendre réel le dénominateur d'une fraction et ainsi poursuivre les calculs.

– v. Conjugués des nombres complexes
– a. Complex conjugate

Conjugué de deux points: Deux points A, B sont conjugués par rapport à deux autres C, D s'ils sont tous alignées et en division harmonique.
– a. Harmonic conjugate

Conjugués isotomiques**: Cas d'intersection de céviennes dans le triangle
– v. Conjugués isotomiques
– a. Isotomic conjugates

Relation de conjugaison des foyers d'une lentille: >>>

Connexe: qui est en liaison avec des choses du même type.

Connexe en topologie: être d'un seul tenant.
– ex. La droite réelle est connexe.
– a. Connected space

Graphe connexe: Un graphe non-orienté est connexe s’il existe une chaine reliant chaque couple de sommets.
Un graphe orienté est fortement connexe s’il existe un chemin reliant chaque couple de sommets.
– v. Vocabulaire des graphes
– a. Connected graphs

Compas: instrument permettant le tracé des cercles.
Aussi, une boussole horizontale
– v. Construction à la règle et au compas
– a. Compass (drawing tool), compass (navigation), straightedge and compass construction, or ruler-and-compass construction

Connecteur logique: mot qui relie des propositions: et, ou, si, alors, non …
Un connecteur logique est un opérateur booléen utilisé dans le calcul des propositions.
– v. Logique formelle, Logique de Boole
– a. Logical connective, logical operator

Connexe*: qui se touche; voisins.
– ex. Des sommets connexes dans un graphe.

Connexe (graphe): graphe non orienté d'un seul tenant.
Pour tout couple de sommets, il existe un chemin du graphe qui les relie.
Aucun sommet du graphe n'est orphelin.
– v. Vocabulaire des graphes
– a. Connectivity in grah theory, connected graph

Connexe (topologie): d'un seul bloc, d'un seul tenant, d'un seul morceau.
– v. Topologie

Conoïde*: surface réglée dont toutes les droites (génératrices) sont parallèles à un plan directeur et passent par une droite (l'axe).
Lorsque le plan directeur et l'axe sont perpendiculaires, le conoïde est dit droit.
– v. Nouveau conoïde de Fermat
– a. Conoid

Coplanaires (vecteurs -): qui sont parallèles au même plan.
– a. Coplanor vectors: Vectors parallel to the same plane, or lie on the same plane.

Consécutif: qui se suivent.
– ex. Les cinq premiers nombres consécutifs sont: 1, 2, 3, 4 et 5.
– v. Nombres consécutifs
– a. Consecutive numbers

Conséquent: en logique, la deuxième proposition, prémisse d'un raisonnement.
– ex. Dans "si A, alors B" , A est l'antécédent et B est le conséquent.
– v. Implication
– a. Antecedent and consequent

Consistance ou cohérence logique**: une assertion ne peut pas être à la fois vraie et non vraie.
Il n'est pas possible de tout démontrer à partir des axiomes de la théorie concernée.
Une théorie est cohérente ou non-contradictoire s'il existe une structure telle que tous les axiomes de la théorie sont vrais dans cette structure.
– v. Incomplétude
– a. Consistency

Constante: quantité dont la valeur est fixe indépendamment de tout contexte.
Pi et e sont des constantes.
– v. Constantes
– a. Constant

Constantes dans une expression: valeurs connues par opposition aux variables.
– ex. Dans ax² + bx + c, x est la variable et a, b et c sont des constantes ou des coefficients.

Constante de proportionnalité: inverse du coefficient de proportionnalité.
Rapport d'un terme de la première suite au terme de même rang de la deuxième suite.
A = {2, 4, 6, 8, …} et B = {6, 12, 18, 24, …}, la constante de proportionnalité est 2/6 = 1/3. et le coefficient est 3.
– a. Proportionality constant. Il semble que les Anglais ne font pas le distinguo entre les deux.

Fonction constante: qui conserve la même valeur quelles que soient les valeurs des variables d'entrée.
Une fonction est constante si et seulement si son image est réduite à un singleton.
Une fonction constante d'une variable réelle est représentée par une droite parallèle à l'axe des abscisses.
La dérivée d'une fonction constante est nulle.
– a. Constant function: output value is the same for every input value

Application constante: Une application d’un ensemble E dans un ensemble F est dite constante si, pour tout couple (x, y) d’éléments de E, on a : f(x) = f(y).
Tous les éléments de E ont la même image: a (a F).
On dit souvent (par abus de langage) que l’application est constante et égale à a.

Constructible (polygone -): polygone régulier constructible à la règle et au compas.
Ils sont constructibles pour n = 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24 …
– v. Constructibles
– a. Constructible

Constructible (nombre -)** : mesure d'un longueur qui est constructible à la règle et au compas en un nombre fini d'étapes.
Tout nombre constructible est algébrique.
– ex. Racine carrée de 2 est constructible, mais la racine cubique, non.
– v. Construction géométrique des nombres
– a. Constructible numbers

Construction à la règle et au compas: exercice, jeu, défi qui consiste à pouvoir dessiner une figure avec ces deux seuls instruments, sans mesurer quoi que ce soit.
– v. Règle, compas
– v. Constructibles
– a. Constructible: Gauss showed that some polygons are constructible but that most are not.
Straightedge and compass construction or ruler-and-compass construction or classical construction,

Contexte mathématique: problème de pure mathématique sans relation avec le monde réel.
– ex. calculez l'hypoténuse d'un triangle rectangle.
Dans un contexte réel, donnez les mesures pour que deux murs soient à angle droit (un classique des maçons: 60, 80, 100).

Continu (caractère -): en statistique, un caractère quantitatif continu prend toutes les valeurs dans un intervalle.
Il faut les numériser pour les rendre discrètes et les traiter.
Il existe deux sortes de caractères quantitatif: les discrets et les continus.
– v. Caractère
– a. Continuous variable, A quantitative variable may be continuous or discrete.

Continu (fraction -) : fraction à étage représentant une constante.
Tout nombre réel (tels que Pi ou e ou le nombre d'or) peuvent être représentés par une fraction continue
– v. Fraction continue
– a. Continued fraction

Continu (fonction -) : si elle ne varie pas beaucoup lorsque la variable varie.
Toutes les fonctions dérivables sont continues; la réciproque n'est pas vraie.
– a. Continuous function: there are no abrupt changes.

Hypothèse du continu: l'infinitude des nombres réels est plus grand que l'infinitude des nombres entiers, et aucun ensemble ne s'intercale entre les deux; rien entre et ;
– v. Aleph, cardinal, diagonale de Cantor
– v. Hypothèse du continu

Continuité notion utilisée pour indiquer qu'une fonction évolue "docilement", sans rupture.
La continuité d'une application f en un point x est le fait que f(y) est de plus en plus proche de f(x) quand y se rapproche de x.
Si une application est continue en tout point de l'intervalle [a, b], alors f(x) prend toutes les valeurs entre f(a) et f(b).
– v. Analyse
– a. Continuity

Solution de continuité = rupture, hiatus.
Attention à cette expression faux-amis
– étym. Latin solutio, solvere: dissoudre, séparation des parties.
– v. Solution de continuité

Continument: (sans accent depuis 1990) Sans aucune interruption.
Chose non divisée ni interrompue du début à la fin.
– ex. l'antenne envoie continument son faisceau vers l'espace.
– a. Continuously

Continuellement: Choses interrompues, mais qui recommencent souvent et à de courts intervalles.
– ex. Il s'acharnait continuellement à trouver une nouvelle méthode.
– a. Continually

Contour: limite d'une figure. Enveloppe de la figure, son périmètre.
– a. Exterior limit of a figure

Contraction, contractile, application contractante*: en topologie, objet susceptible de se contracter selon certaines règles.
– v. Topologie
– a. Contracting mapping or contraction

Contradiction: lorsque une proposition se retrouve vraie et fausse à la fois; une contradiction existe lorsque deux affirmations, idées, ou actions s'excluent mutuellement;
la contradiction est une relation existant ente deux ou plusieurs termes ou deux ou plusieurs propositions dont l’une affirme ce que l’autre nie; A et non-A sont contradictoires;
ex: tous les moutons du troupeau sont blancs et j'ai vu un mouton noir dans le troupeau.
– v. Tiers exclu
– a. Contradiction, law of excludes middle

Contrainte: force appliquée sur une surface donnée à l'intérieur d'un corps.
– a. Stress
Étirement : contrainte de tension.
Écrasement: contrainte de compression.
Cisaillement: forces opposées s'exerçant sur les côtés opposés d'un matériau.

Contrainte: en mathématique et notamment en optimisation linéaire, condition restrictive imposée à une ou des variables numériques ou géométriques.
– a. Constraint, linear optimization problems

Contraire (événement -): en probabilité, un événement et son contraire ne peuvent pas se produire ne même temps, mais la probabilité des deux réunis est certaine (égale à 1).
Le contraire d'un événement est son complémentaire dans l'ensemble des possibles.
– v. Probabilité
– a. Complementary event: the complement of any event A is the event not A.

Contraire (propositions -): deux propositions contraires s'appliquent à l'ensemble tout entier, indépendamment du fait qu'elle soit vraie ou fausse.
Les deux propositions peuvent être fausses en même temps, mais pas vraies en même temps.
– ex. Tous les moutons sont noirs et aucun mouton n'est noir.
– v. Contradictoire
– a. Square of opposition
– type de propositions:

Contraposée*
Si a Þ b (a implique b ou si a alors b), la proposition contraposée est (non b) Þ (non a).
– ex. La proposition contraposée de la proposition « s'il pleut, alors le sol est mouillé » est « si le sol n'est pas mouillé, alors il ne pleut pas ».
– v. Implication
– a. Contraposition
Réciproque de: si A alors B: si B alors A
Contraposée de: si A alors B: si non B, alors non A

Contre-exemple: un seul exemple qui suffit à infirmer une propriété supposée (conjecturée).
– ex. Tous les nombres premiers sont impairs. Non, car 2 est premier et pair (même s'il est le seul premier pair).
– v. Conjecture (fausse) de De Polignac, conjecture (fausse) de Polya.
– a. Counterexample: any exception to a generalization, counter-proof

Convergente (suite -): La suite U_n est convergente si elle admet une limite quand n tend vers l'infini.
– notation:
– v. Suite, divergente
– a. If a limit exists, the sequence is called convergent; if not: divergent .

Convergent (procédé -): procédé (algorithme) de calcul itératif, qui à partir d'une valeur initiale, finit par approcher une valeur limite, solution du problème cherché. La convergence est plus ou moins rapide.

Conversion d'unités, de mesure: Passage d'une unité de mesure à un autre par application de coefficients.
– v. Conversion des unités
– v. Conversion of units, conversion factor

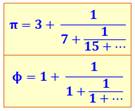
Convexe: synonyme de sortant, qui présente une bosse.
– v. Concave (antonyme)
– a. Concave and convex

Objet convexe: tel qu'un segment de droite qui relie deux points quelconques de cet objet est entièrement à l'intérieur de cet objet.
Les polygones ou polyèdres réguliers sont convexes. Un polygone convexe est situé entièrement d'un seul côté d'une ligne passant par chacun de ses côtés. Un polyèdre convexe est situé entièrement d'un seul côté d'un plan passant par chacun de ses faces.
Autre propriété: en parcourant le périmètre de la figure dans le sens horaire par exemple, on pivote toujours dans le mêmes sens (la droite, par exemple) pour tracer le côté suivant.
– v. Icosagone

Objet concave: non convexe.
– mnémotechnique: idée d'une courbe convexe dans un verre, courbe qui monte, comme la bouche du smiley triste L (celui qu'on vexe est triste!) alors que concave va, bien content, à la cave J.

Fonction convexe**: soit une fonction définie sur un intervalle (a, b) de ℝ et soit (C) sa courbe représentative. Si M est le point de (C) d’abscisse x et N le point de (C) d’abscisse y, on dit que la fonction est convexe si, pour tout nombre z compris entre x et y, le point de (C) d’abscisse z (P) est situé au-dessous du point Q de la droite MN qui a pour abscisse z.
– ex. f(x) = x² : fonction convexe; f(x) = x³ : fonction non convexe sur un intervalle de la forme (- a, + a).
– a. Convex function

Convolution (produit de -)**: produit entre deux fonctions qui en donne une sorte de moyenne glissante.
Opération sur deux fonctions qui en produit une troisième, laquelle reflète comment la forme de l'une est modifiée par l'autre.
On utilise ce produit en électronique pour l'écriture des filtres passe-bande.
En mathématiques, il sert à approximer et régulariser des fonctions.
– v. Multiplication rapide
– a. Convolution

Coordonnées: valeurs lues sur les axes d'un graphique muni d'un système d'axes (x, y, z …) et qui suffisent pour déterminer la position d'un point.
– types: cartésiennes, polaires, cylindriques, sphériques, homogènes.
– v. Abscisse (x), ordonnée (y), et cote (z).
– v. Coordonnée
– a. Coordinates, abscissa, ordinate, applicate

Système de coordonnées: il permet la représentation de point dans le plan ou l'espace.
– illustartion: Système de coordonnées tridimensionel (ou 3D)
– v. Repère, base, référentiel
– a. Coordinate system, three-dimensional coordinate system, 3D coodinate system

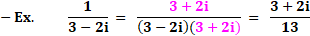Coordonnées cartésiennes: coordonnées dans un repère orthonormé.
Tout point du plan peut être repéré par deux nombres réels appelés abscisse et ordonnée.
La troisième coordonnée pour l'espace est la cote (Illustration).
– v. Cartésien
– a. Cartesian coordinate system or rectangular coordinate system or orthogonal coordinate system

Coordonnées du milieu d'un segment: soit les extrémités du segment A(x, y) et A'(x', y'), les coordonnées de M, milieu du segment AB, sont (x + x') / 2 et (y + y') / 2.
– v. Théorème du point mileu
– a. Midpoint coordinates of a segment

Coplanaires (vecteurs -): qui appartiennent au même plan ou à des plans parallèles.
– v. Colinéaire et coplanaire

Copremiers: se dit de nombres premiers entre eux.
Nombres dont le seul facteur commun est 1.
Nombres dont le PGCD est égal à 1.
– a. Coprime, mutually prime or relatively prime.

Copte: langue descendant de l'égyptien ancien.

Copule**:
En linguistique, mot qui lie le sujet d’une proposition avec l’attribut. En français, le verbe être est une copule.
En logique, c'et le verbe être qui lie le prédicat au sujet.
En théorie des probabilités, la copule est utilisée pour décrire la dépendance entre variables aléatoires sans se préoccuper de ses lois marginales.
– étym. ne latin, copula signifie: lien, laisse, union. De cum avec et apere, attacher.
– a. Copula

Corde: segment dont les extrémités appartiennent à une courbe, un cercle…
Une corde d'un cercle est un segment qui joint deux points du cercle; une corde sous-tend deux arcs de cercle.
Une corde qui passe par le centre du cercle est un diamètre.
Une corde prolongée est une sécante
En théorie des graphes: arête reliant deux sommets non-adjacents d'un cycle.
– v. Cordes, partage du cercle par ses cordes
– a. Chord

Corde focale: corde qui passe un point focal d'une conique (parabole et ellipse).
La corde latus rectum est une corde focale perpendiculaire à l'axe principal de la conique.
– a. Focal chord: a chord that passes through the focus of a parabola or an ellipse.

Cornet: solide formé de l réunion d'un cône régulier à base circulaire et d'une demi-sphère.
Image d'un cornet à glace surmonté d'une boule.
– a. Volume: h hauteur du cône et R rayon du cercle.
– a. Cone mounted over hemisphere

Corollaire: propriété découlant naturellement d'une propriété déjà démontrée.
Conséquence directe d'un théorème.
– v. Démonstration, théorème, axiome, hypothèses, etc.
– a. Corollary: a theorem of less importance

Corps* ensemble de nombres stable par division. Par exemple, l'ensemble des nombres complexes dont la partie réelle et la partie imaginaire sont des rationnels est un corps de nombres; Ensemble ayant deux lois de composition interne, dont la première lui donne une structure de groupe commutatif et la seconde donnant aux éléments non nuls la structure de groupe, et de plus la seconde loi étant distributive par rapport à la première
– v. Corps, anneau, vocabulaire des structures algébriques
– a. Field: set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers do.

Corps	Corps convexe	Corps Fini	Corps gauche, algèbre à division
*Field*	*Convex body*	*Galois field, finite field*	*Division algebra, division ring, skew field*

Corps quadratique**: famille des nombres de la forme a + b .
Il est noté Q().
Les nombres a et b sont rationnels (Q) et k est un entier positif sans facteur carré.
Si k est négatif, on a Q() avec des nombres de la forme a + ib.
– ex. Q() regroupe tous les nombres en a + b avec a et b rationnels.
– a. Quadratic field

Corps fini ou corps de Galois**: famille de polynômes en quantité finie via les congruences.
Manière de passer du monde infini des polynômes à un monde fini.
– ex. avec le premier degré, il n'existe que deux polynômes: x et x + 1.
– v. Corps de Galois, polynômes irréductibles
– a. Galois field (GF)

Corrélation* propriété de ce qui est très lié.
Liaison entre deux caractères (corrélation simple) ou plus (corrélation multiple) telle que les variations de leurs valeurs soient toujours de même sens (corrélation positive) ou de sens opposé (corrélation négative).
– a. Correlation

Coefficient de corrélation entre deux variables numériques: il est égal au rapport de leur covariance et du produit non nul de leurs écarts types. Il est compris entre -1 et 1.
– v. Big Data
– a. Correlation coefficient

Correspondants (angles -): angle d'un même côté d'une sécante à deux droites parallèles
– v. Types d'angles, alternes internes
– a. Corresponding angles

Côtés correspondants ou homologues: côtés dans la même disposition pour les figures semblables (Illustration).
Leurs longueurs sont proportionnelles ou égales si les figures sont isométriques.
– a. Corresponding sides, in similar figures, the corresponding sides are proportional in length

Cosécante: inverse du sinus;

– v. Trigonométrie
– a. Cosecant

Cosinus: dans un triangle rectangle et pour l'un des angles, valeur du rapport de la longueur du côté adjacent à celle de l'hypoténuse (pour retenir: cosinus avec le côté à côté ); ex:

– v. Trigonométrie, sinus, loi des cosinus
– a. Cosine

Cotangente: égal inverse de la tangente; cotg = 1/ tangente = cosinus / sinus.

– v. Trigonométrie
– a. Cotangent

Côté: chacun des segments délimitant un polygone, ou un angle.
Désigne aussi la mesure de ce segment (un côté de 5 cm).
– v. Adjacent, opposé, arête
– v. Bases de la géométrie
– a. Side

Cote: valeur lue sur la ligne verticale (z) d'un repère tridimensionnel.
– proches: Abscisse, ordonnée
– v. Coordonnées
– a. Applicate: The z-coordinate, similar to abscissa and ordinate for the x- and y-coordinates, respectively.

Côtés de l'angle: chacune des demi-droites formant l'angle.

Côtés du polygone: chacun des segments formant le polygone.

Côtés du polyèdre: chacune des faces formant le polyèdre.
– a. Side. Edge = arête

Côtés homologue: synonyme de côtés correspondants.

Cototient* ou co-indicatrice d'Euler de n: quantité de nombres ayant un facteur commun avec n.
– a. Euler's cototient function.

Couple: deux nombres ou deux objets dans l'ordre indiqué; c'est donc une paire ordonnée.
– notation: (9, 8)
– propriété: (a, b) = (c ,d) ssi a = c et b = d.
– v. Doublet, bipoint, k-tuple, paire
– a. Ordered pair

Couple: objet mathématique formé à partir de deux objets x et y, que l’on note (x, y). x s’appelle première composante du couple et y deuxième composante du couple.

Deux couples (x, y) et (x’, y’) sont égaux si et seulement si x = x’ et y = y’.

Donc, en général, si x et y ne sont pas égaux, les deux couples (x, y) et (y, x) sont distincts.

Parfois, pour insister sur cette importance de l’ordre des éléments x et y, on donne le nom de couple ordonné à un couple.

Coupure de Dedekind**: manière de définir (de construire) les nombres réels.
Moyen de caractériser un nombre (un réel) en le situant dans un intervalle de nombres connus (rationnels).
– ex. le nombre racine de 2 (réel) est situé entre 41/29 et 99/70 (par exemple). On peut affiner et ainsi, racine de 2 est défini par l'ensemble des nombres rationnels qui lui sont inférieurs et par celui de ceux qui lui sont supérieurs.
La définition formelle n'est pas limitée aux nombres.

Courbe ou ligne courbe: ligne dessinée par un point qui se déplace continument dans le plan, sans rebroussement.
– v. Courbes élémentaires, arc de cercle
– a. Curve or curved line: not a straight line

Courbe en cloche ou courbe de Gauss: v. Normale

Courbe paramétrée: v. Paramétrée

Courbe de Jordan: courbe fermée simple (continue et lisse).
– v. Problème du rectangle inscrit

Courbe de niveau: v. Ligne de niveau

Une courbe (objet à une dimension) dans un espace à n dimensions est caractérisée par trois paramètres:

Dimension de l'espace: D = 2, 3, 4 …

Degré de la courbe: quantité de fois que la courbe traverse l'espace D – 1; et

Genre: quantité de trous.

Courbure: inverse du rayon du cercle osculateur à une courbe.
– v. Courbure
– a. Curvature

Couronne (circulaire): surface comprise entre deux cercles concentriques.
– v. Couronne, couronne magique, couronne en or et Archimède.
– a. Annulus (pl. annuli): region between two concentric circles.

Covariance*: nombre permettant d'évaluer le sens de variation de deux variables aléatoires (ou de deux séries de données numériques) et, ainsi, de qualifier l'indépendance de ces variables.
Si deux variables aléatoires sont indépendantes alors leur covariance est nulle, mais la réciproque est fausse.
– v. Corrélation
– a. Covariance: a measure of the joint variability of two random variables

CQFD: ce qu'il fallait démontrer.
Du latin QED Quod Erat Demonstratum; indique la fin d'une démonstration;
N'est plus guère utilisé.
La fin d'une démonstration est parfois notée

Cramer (système de -, règle de -, ou méthode de -):
Système de n équations linéaires à n inconnues ayant une solution unique.
– v. Système d'équations
– a. Cramer's rule

Crédit: en comptabilité, c'est la somme que l'on me doit et je crois que je vais être remboursé un jour; partie d'un compte qui mentionne les sommes dues; c'est un avoir, une créance;
Il me doit de l'argent: je suis son créancier, il est mon débiteur.
– étym. Latin creditum, de credere, croire:
– Contraire: débit
– v. Solde, balance, bilan

Crible d'Ératosthène: façon de trouver les nombres premiers par élimination successives des multiples de 2, 3, 5, 7 …
– v. Crible d'Ératosthène, crible de la roue
– a. Sieve of Eratosthenes: an algorithm for finding all prime numbers up to any given limit.

Crible (théorie des cribles) : généralisation aux méthodes permettant de dénombrer ou d'estimer la quantité d'éléments dans un sous-ensemble de nombres entiers. Une branche de la théorie des nombres.
– v. Cribles – Types
– a. Sieve theory

Critère de divisibilité ou caractère de divisibilité: règle qui permet de déterminer si un nombre est divisible par un autre nombre donné.
– ex. un nombre est divisible par 3 si la somme de ses chiffres est divisible par 3;
– v. Divisibilité, critères de divisibilité par un nombre k

Critère: synonyme de caractère.

Crochet: [ ]
– a. Square bracket

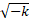
Croisé (quadrilatère -): dont les côtés se croisent (Illustration).
S'applique aussi aux polygones.
– v. Quadrilatère
– a. Crossed quadrilateral or complex quadrilateral: the quadrilateral has self-intersecting sides

Croissant (ordre -): qui va du plus petit vers le plus grand.
– v. Décroissant, ordre
– a. Decreasing and increasing order

Croix (produit en -) ou règle de trois: si alors, nous avons l'égalité du produit en croix ad = bc;
Produit intéressant car, si trois valeurs sont connues, il permet de calculer la quatrième proportionnelle.
– v. Règle de trois et quatrième proportionnelle
– a. Cross-multiplication

Cryptage: synonyme de chiffrement.
– a. Encryption, cypher

Cryptarithme: en récréation mathématique, opération formée de lettres à remplacer par des chiffres de façon à rendre l'opération exacte.
– v. Cryptarithme, alphamétique

Cryptographie: comment écrire des messages secrets, que personne ne peut comprendre sauf le destinataire; ensemble des techniques permettant de protéger une communication au moyen d'un code graphique secret; vient du grec kruptos, caché, et graphein, écrire
– v. Cryptologie, chiffrement
– a. Cryptography

Cube: volume dont les six faces sont carrées et égales comme le dé à jouer; parallélépipède rectangle à face carrées égales; les 12 arêtes sont aussi de même longueur
– v. Cube, polyèdre
– a. Cube: a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex.

Cube d'un nombre: ce nombre a multiplié par lui-même trois fois, noté a³ (1 000 est le cube de 10 car 10 x 10 x 10 = 1 000); 27, 64, 125 sont des cubes parfaits
– v. Puissance, carré, racine
– v. Nombres cubes.
– a. Cube: the third power of a number. Élever au cube: to cube

Cube parfait: nombre qui est le cube d'un nombre naturel.
– ex. 27 qui est égal à 3³.
S'applique aux nombres et non pas aux expressions mathématiques.
– ex. x³ – 3x² + 3x – 1 qui est égal à (x- 1)³ est le cube du binôme (x – 1).
– a. Perfcect cube

Cube de Rubik: casse-tête géométrique tridimensionnel composé de 26 petits cubes visibles, inventé en 1974 par le Hongrois Erno Rubik.
– v. Cube de Rubik
– a. Rubik's cube

Hypercube: analogue au cube en quatrième dimension.
L'hypercube est au cube ce que le carré est au cube.
L'hypercube est l'un des six polytopes réguliers convexes.
– v. Hypercube, tetracube
– a. Tesseract

Cubique: propriété relative au cube.

Racine cubique: nombre tel que multiplié trois fois par lui-même restitue le nombre d'origine.
– notation et exemple:
– a. Cubic root

Courbe cubique: une courbe cubique est une courbe algébrique plane définie par une équation du troisième degré.
– a. Cubic plane curve

Équation cubique: équation polynomiale de degré 3, de la forme ax³ + bx² + cx + d = 0 avec a non nul, où les coefficients a, b, c et d sont réels ou complexes.
– v. Équation du troisième degré – Résolution
– a. Cubic equation

Cumulées (valeurs – ou somme -): dans une suite de nombres et pour l'un d'eux, se dit de la somme de tous les nombres qui précédent; ex: suite (1, 2, 3, 4) et valeurs cumulées (1, 3, 6, 10).
– v. Somme des entiers
– a. Cumulative value or sum

Cumulé (effectif -): somme de toutes les valeurs des caractères précédents.
– ex. Effectifs cumulé pour "18 ans" = toutes les personnes dont l'âge est inférieur ou égal à 18 ans.
– a. Cumulated headcount, combined headcount

Cuspide ou point de rebroussement: point singulier sur une courbe avec changement de direction.
– a. Cusp

Curviligne (figure -): figure formée par les lignes courbes.
– ex. triangle curviligne.
– a. Figure made up of curved lines

Curviligne (intégrale -)*: intégrale dont la valeur est la somme sur chaque point de la courbe avec pondération par une fonction scalaire (une longueur d'arc par exemple). C'est cette pondération qui distigue l'intégrale curviligne de l'intégrale simple.
– a. Line integral, contour integral, path integral

Cybernétique: au sens (trop) strict: étude des systèmes asservis.
Plus généralement: science de l’information captée, transmise, stockée, et enfin élaborée c’est-à-dire soumise au calcul.
Science à l'origine de l'informatique.
– v. Cybernétique
– a. Cybernetic

Cycle d'un graphe: synonyme de boucle dans un graphe.
– a. Cycle: a closed walk (also called a tour) or more specifically a closed walk without repeated vertices

Cyclique: qui se répète régulièrement.
Nombres cycliques ou périodiques.
– ex. 1/7 = 0,142857142857… 142857 est la période
– a. Number with Repeating or recurring decimals

Nombre cyclique ou nombre phénix ou nombre têtu: nombre dont les permutations circulaires des chiffres correspondent aux multiples du nombre.
Période des nombres cycliques longs.
– ex. 142 857 × 2 = 285 714; 142 857 × 3 = 428 571; etc.
– v. Nombres phénix, nom des nombres
– a. Cyclic number

Cocycliques (points -): les sommets d'un quadrilatère inscriptible (tous sur le même cercle) sont dits cocycliques. Le cercle est circonscrit au quadrilatère.
– v. Cocyclique
– a. Concyclic points or cocyclic points: they lie on a common circle

Cycliques (quadrilatère -) ou quadrilatère inscriptibles: dont les quatre sommets sont situés sur un cercle.
– v. Théorème de Ptolémée
– a. Cyclic quadrilateral or inscribed quadrilateral: a quadrilateral whose vertices all lie on a single circle

Cycloïde ou roulette: trajectoire de la valve d'une roue de voiture (ou de tout autre point de la roue).
Lieu géométrique d’un point fixe M d’un cercle (C) qui roule, sans glisser, sur une droite 0x.
–v. Cycloïde
– a. Cycloid

Cylindre: solide qui a la forme d'un tube, d'un rouleau.
Plus généralement, un solide engendré par le mouvement d'une droite (génératrice) qui s'enroule sur une courbe (directrice).
Si la courbe directrice est un cercle, le cylindre est de révolution.
Si la droite génératrice est perpendiculaire au plan du cercle, le cylindre est droit.
–v. Cylindre
– a. Cylinder: right circular cylinder, oblique circular cylinder, eliptical cylinder.

Ensemble des droites parallèles à une droite (D) et rencontrant une courbe (C). Les droites sont appelées les génératrices du cylindre ; la courbe (C) est appelée directrice du cylindre. Si la courbe (C) est un cercle et si les génératrices sont parallèles à l’axe du cercle, le cylindre est appelé cylindre de révolution.

Cylindre droit de révolution: le cylindre classique, souvent appelé cylindre tout court.
–v. Cylindre droit
– a. Right circular cylinder

Cypher: mot anglais ayant plusieurs sens.
– Nombre, monogramme, code, système de codage, un message codé.
– Bloc de trois chiffres. Ex. 1,000,000 is a number having two ciphers of zeros
– étym. Du vieux français cifre pour chiffre; de l'arabe sifr, zéro, vide.

>>> D

Voir	Atlas des maths – des références Débutants – pour juniors ou novices
Aussi	DicoNombre – tous les nombres de 0 à l'infini DicoLettre – signification des lettres en maths et ailleurs DicoCulture lettre C
Autres	Voir page des liens et références
Cette page	http://villemin.gerard.free.fr/Referenc/Encyclop/C.htm