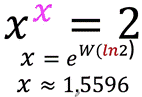![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page |
|
22 Novembre 2025
![]()
|
Édition du: 29/11/2025 |
|
INDEX lettre L |
Dictionnaire de base du vocabulaire des mathématiques |
|
|
Faites
un double-clic pour un retour en haut de
page
Pour
trouver un mot: Ctrl F et tapez le mot
cherché
|
Avertissement Dictionnaire pour débutants,
juniors, novices, "nuls" … !!! On privilégie la compréhension par rapport à une rigueur mathématique !!! Les liens permettent de compléter et d'approfondir Pour une
version plus académique se reporter aux ouvrages spécialisés |
Légende Parfois,
plusieurs définitions sont données: de la plus "intuitive" à la
plus correcte mathématiquement Mode de recherche: si vous ne trouvez
pas symétrie centrale à symétrie, voyez à centrale, par exemple. Difficulté: * notion avancée;
** notion complexe. |
![]()

Labyrinthe: tracé sinueux, muni
ou non d’embranchements, souvent destiné à égarer celui qui s’y engage.
– v. Labyrinthe
– a. Maze
Lacet: mouvement de gauche
à droite ou inversement d'un véhicule (navire, avion).
Pensez à l'angle de virage en voiture.
– v. Degrés de liberté, tangage, roulis
– a. Yaw
Mouvement d'oscillation d'un véhicule autour d'un axe vertical, passant
par son centre de gravité. Commandé par le palonnier
dans un avion. Le palonnier est constitué de deux pédales qui permettent d'actionner la gouverne de direction.
 – Voir site: Les gouvernes de vol
– L'avionnaire – On y trouve des figures
explicites
– Voir site: Les gouvernes de vol
– L'avionnaire – On y trouve des figures
explicites
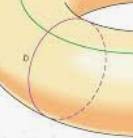
Lacet (topologie): chemin
fermé. Voir illustration
– a. Loop
(littéralement: boucle), closed curve, closed path, circuit
Lacune: trou, absence d'un
objet qui semble pourtant nécessaire.
– ex. série lacunaire,
dont un grand nombre de coefficients sot nuls.
– a. Gap
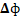 Lambert (fonction W de -) ou
fonction Oméga**: notion impliquée dans la résolution d'équation où l'inconnue est en
exposant.
Lambert (fonction W de -) ou
fonction Oméga**: notion impliquée dans la résolution d'équation où l'inconnue est en
exposant.
– def. ![]()
– v. Nombre
1,5596…, Lambert
– a. Lambert W function
Langage
binaire ou système binaire: utilisation de la numération binaire comme
moyen d'expression notamment dans les ordinateurs.
– a. Binary language
Au plus profond de l'ordinateur, les circuits
"discutent" entre eux dans ce mode: échanges de 0 et de 1 dont la
signification est convenue par le concepteur de l'ordinateur. Les nombres décimaux sont facilement codés en
binaire; les lettres font l'objet
d'une table de correspondance (ASCII, par exemple); Le travail de l'ordinateur
est une suite d'instructions qui,
elles aussi, sont codées en binaire. Devant votre clavier vous envoyez des
informations qui sont traduites (compilées) par étapes successives pour aboutir
à de longues listes de mots binaires.
Langlands Program**: notamment, une recherche d'une manière de relier chaque groupe de Galois (relatons entre les racines d'un
polynôme) avec des formes automorphiques (formes qui se
reproduisent elles-mêmes).
Plus généralement, recherche de structures internes de haut niveau entre divers
objets mathématiques.
C'est une collection de conjectures et de théorèmes interconnectés à propos des
relations entre la théorie des nombres, la géométrie et l'analyse.
– intérêt: il est parfois plus facile de
démontrer une propriété dans le monde image (par transformation automorphique)
que dans le monde d'origine.
– citation: Le programme Langlands est un
ensemble de conjectures
qui touchent presque tous les domaines des mathématiques pures – Ana Caraiani,
Imperial College London.
– v. Programme de Langlands,
perfectoïde, nombres
p-adiques, théorie des représentations, mathématiques condensées
Le programme Langlands a débuté en 1967, lorsque son homonyme, Robert
Langlands, a écrit une lettre à un célèbre mathématicien nommé André Weil.
Langlands a proposé qu'il devrait y avoir un moyen de faire correspondre chaque
groupe de Galois avec un objet appelé une forme automorphe. Alors que les
groupes de Galois apparaissent en algèbre (reflétant la façon dont vous
utilisez l'algèbre pour résoudre des équations), les formes automorphes
proviennent d'une branche très différente des mathématiques appelée analyse,
qui est une forme améliorée de calcul.
Laplacien (opérateur
-)**: opérateur différentiel du deuxième degré: application de l'opérateur
gradient suivie de l'application de l'opérateur divergence.
– symbôle: ![]() .
.
– v. Équations de Navier-Stokes
(utilisation), gradient, divergence
– a. Laplace operator
Largeur:
plus
petite dimension du rectangle;
la plus grande étant la longueur. Convention de langage, sans caractère de
qualité. Longueur et largeur sont des longueurs de segments.
– a. Width / al. Breite (f)
L'aire du rectangle est
égale au produit de la largeur par sa longueur. Un nombre est premier s'il est impossible de lui
trouver un rectangle dont l'aire à une largeur supérieure à 1. Ex: 8 = 4 x 2 n'est pas premier, mais 7 = 7 x 1 est premier. Autrement-dit: avec un nombre
premier, il est impossible de faire une multiplication autre qu'avec le nombre
1.
Latéral: synonyme de sur les côtés, sur les flancs;
– ex. Les faces latérales de la pyramide. Face qui ne joue pas le rôle de base
– éty. Du latin: latus côté
– a. Lateral face of the pyramid
LaTeX: outil d'écriture
linéaire de formules mathématiques.
Avec Word, l'outil
"insertion équation" permet l'écriture immédiate de formules.
Le logiciel GeoGebra utilise le
langage LaTeX et c'est un outil pratique (et gratuit) pour l'écriture les
formules.
– ex. écriture LaTex sur la ligne du haut et sa représentation classique sur la
ligne du bas:
Latin (carré -): grille carrés remplies
de nombres (ou objets), un objet unique sur chaque ligne et sur chaque colonne
– v. Carré latin, mathématique
des carrés latins, carré gréco-latin,
carré magique,
sudoku
– a. Latin square
Latitude: coordonnée
géographique sud-nord; angle entre la verticale d'un lieu et le plan de
l'équateur. Plus précisément: La latitude est une des coordonnées sphériques
d’un point de la surface terrestre définie par la distance angulaire de ce
point à l’équateur.
– ex. la France est située autour de la latitude 45° Nord.
– v. Sphère terrestre, longitude, parallèle, GPS.
– a. The location's latitude/longitude
coordinates.
Tous les points de la Terre de même latitude forment un cercle nommé parallèle. Ce cercle imaginaire est, en effet,
inscrit dans un plan parallèle à celui de l'équateur. Les parallèles sont des loxodromies,
et ne sont donc pas la plus courte distance entre deux points.
Latus rectum: segment de droite
qui relie deux points d’une conique, qui est
perpendiculaire à l’axe principal de la conique et qui passe par le foyer de
cette conique.
– éty. Du latin: côté droit
Lean: logiciel de haut
niveau (compréhensible par l'homme) dont une des applications majeures est la
vérification des preuves en maths.
Ce logiciel est accompagné d'une base de données (mathlib) de plus de 70
000 théorèmes.
– v. Outils de programmation,
trois types
de logiciels
– a. Theorem-proving programs
Lemme: sorte d'étape
préliminaire à une démonstration.
Proposition
déduite d'un ou de plusieurs postulats dont la démonstration
prépare celle d'un théorème.
Un lemme est un petit théorème de nature technique.
– en pratique, c'est une sorte d'aparté qui allège la démonstration principale.
– ex. Lemme d'Euclide-Gauss / Exemple de lemme**.
– v. Démonstration, théorème,
axiome, hypothèses, etc.
– mnémo. Deux lemmes = dilemme (avec
deux m) !
– ety. Du grec lêmma: résultat, recette, conséquence.
– a. Lemma
 Lemniscate: figure en forme de huit couché, symbole de l'infini. Illustration
Lemniscate: figure en forme de huit couché, symbole de l'infini. Illustration
Lentille: figure géométrique
en forme d'amande. Intersection de deux cercles de même rayon.
– v. Géométrie de la lentille, vesica piscis,
– a. Lens
Lettres grecques:
–
ex. Alpha, béta, delta, mu, epsilon, pi,
sigma, zêta, oméga …
– v. Alphabet grec
/ Lettres
symboles en maths
– a. Greek alphabet
Lettres hébraïques:
– v. Alphabet hébreux / Lettres symboles en
maths / Aleph et
infini
– a. Hebrew alphabet
LHS: Left hand side, la
partie gauche d'une équation, par exemple.
RHS: right hand side.
Lie
(Groupes de Lie)**: groupes de transformations de l'espace qui en
préservent la structure géométrique lors de petits déplacements, comme la
rotation du cercle.
– Notion de groupes
de symétries.
– v. Groupe de Lie
– a. Lie group
Lieu géométrique: ensemble de points
vérifiant une propriété géométrique donnée.
– ex. le cercle est le lieu des points à égale distante d'un point donné, le
centre du cercle.
– a. Locus: the set of points satisfying a particular condition, often forming
a curve.
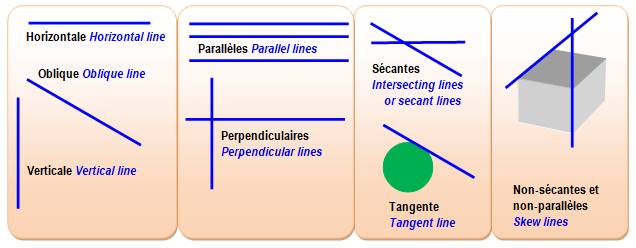
Ligne: figure qui a une
longueur mais pas d'épaisseur.
Trait continu à l'image d'un mince fil de couture.
Lieu où deux surfaces se coupent.
Un point qui se déplace engendre une ligne.
La ligne est une entité géométrique de dimension 1.
– v. Éléments de base de
la géométrie
– a. Line: a one-dimensional geometric figure with length but no width.
Types de lignes
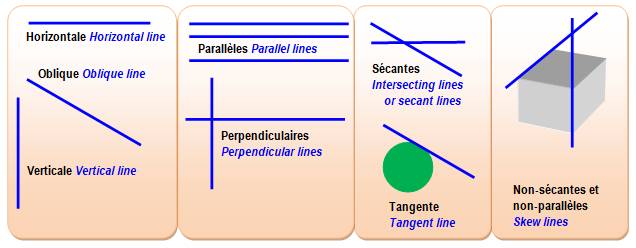
Ligne droite (une droite): tracé droit passant
par deux points; image du fil tendu;
Le segment entre les deux points constitue la plus courte distance entre deux
points.
– v. Droite
– a. Straight line, line segment, curved
line
Demi-droite: une ligne droite limitée à une extrémité est
une demi-droite; limitée aux deux extrémités, c'est un segment.
– a. Ray: A ray is part of a line
that extends without end in one direction. It starts from one endpoint and extends forever in one direction.
Ligne brisée ou ligne polygonale: ligne formée d'une
suite de segments adjacents, appelés arêtes.
– a. Polygonale chain: a connected series of line segments.
Ligne courbe (une courbe) : ligne continue
toute en arrondis; sans point anguleux.
– v. Courbes élémentaires
– a. Curved line
Ligne de tableau: rangée horizontale dans un tableau, dans un carré magique ou
dans une matrice
…
– v. Colonne
 – a. Row: things lying side-by-side. Objects, people, numbers, etc in a
horizontal line.
– a. Row: things lying side-by-side. Objects, people, numbers, etc in a
horizontal line.
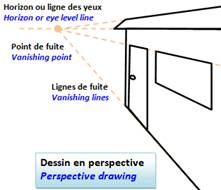
Ligne de fuite: dans une perspective simple, il y a un seul point de fuite où
toutes les lignes de fuite convergent.
– a. Vanishing lines, converging lines,
perspective drawing, vantage point (point de vue)
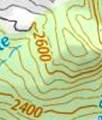
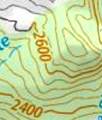
Ligne ou courbe de niveau: ligne de même altitude sur une carte géographique.
Llieu des points tel que l'application
donne une valeur constante: f(x) = k
– a. Contour line
|
L'étude du relief via les courbes de niveau
se nomme l'orographie (du grec: oros, la
montagne). Les lignes ou courbes de niveau sont aussi désignées par lignes orographiques. Notez que le
haut des nombres d'altitude montre la direction du sommet. |
|
Limite; valeur telle que
l'écart entre cette valeur et la fonction est arbitrairement petite.
– Notation: ![]() Ce qui veut dire que l'on peut rendre f(x) aussi proche de L que l'on
veut, sur un intervalle aussi petit soit-il autour de a.
Ce qui veut dire que l'on peut rendre f(x) aussi proche de L que l'on
veut, sur un intervalle aussi petit soit-il autour de a.
– v. Limite définition, limite développements, analyse, asymptote.
– a. Limit, limit of a function, right-end limit, left-hand limit, lower
boundary, upper boundary.
– Définition

Linéaire
(application ou opérateur ou transformation ou fonction -): application
f(x) = ax, représentée par une droite.
Plus généralement une application du type f = a1x1 + a2x2
+ a3x3 + …
– v. Affine
– a. Linear map, linear mapping, linear transformation, vector space
homomorphism, or linear function
Inégalité linéaire: inégalité
qui implique une fonction linéaire.
– ex: 3x – 2y > 5
– a. Linear inequality
Inégalité matricielle linéaire: inégalité linéaire
dont les coefficients sont des matrices.
– a. Linear matricial inequality (LMI).
Linéaire (combinaison -): ensemble de termes
sommés après multiplication par un coefficient.
Les termes forment un vecteur et les coefficients sont des scalaires.
– a. Linear combination: an expression
constructed from a set of terms by multiplying each term by a constant and
adding the results.
Expression algébrique faite d'une somme de
termes, résultant du produit d'un vecteur dont chaque terme est pondéré par un
scalaire. Soit la forme: ax + by … + c = 0.
Plus généralement, il s'agit d'une application linéaire valant une constante a1x1
+ a2x2 + a3x3 + … = c.
Linéaire (algèbre -): étude des
transformations linéaires, des systèmes d'équations
linéaires, des espaces vectoriels.
– a. Linear algebra
Linéaire (espace -) ou espace
vectoriel*: ensemble munis de deux opérations: addition et multiplication par un
scalaire.
– v. Espace vectoriel
Linéaire (programme -): résumé d'un problème particulier, comme
l'optimisation de la production d'objets, sous la forme d'un système
d'équations.
– Exemple
en Illustration.
Résolution algébrique ou graphique et parfois, pour les cas complexes, par
utilisation de la méthode
de Simplex ou de la Méthode de Monte-Carlo
Linéarisation
Linéarisation en algèbre: c'est trouver une fonction linéaire (affine) la plus proche de la
fonction considérée.
– syn. Approximation affine
– a. Linearization, linear approximation to a function at a given point.
Linéarisation en géométrie: c'est trouver la
ligne ayant même longueur qu'une courbe.
– a. Linear approximation, approximation of curves by line segments
Linéarisation en trigonométrie**: c'est transformer des produits et des
puissances en une somme de termes chacun élevé à la puissance 1.
– Exemples: ![]()
–
v. Linéarisation en trigonométrie
– a. Power reducing formulas for trigonometric functions
Linéarisation en informatique: c'est transformer une information en une suite de
nombres.
Codage d'une information sous la forme d'une suite d'informations plus petites
dites atomiques.
– Syn. sérialisation, encodage.
Contraire: désérialisation
– a. Serializationor marshalling; unmarshalling
Liste: Énumération dans
l'ordre d'éléments, d'objets, d'opérations, de mots, etc.
En informatique, on accède à un élément de la liste en précisant son rang.
– Ex: L = [a, z, table, bidule].
– voisins: Ensemble, suite, série, tuple
– v. Liste
– a. List
Littéral: avec un calcul
littéral (ou calcul algébrique), les nombres sont remplacés par des lettres.
– Syn. calcul algébrique
– v. Bases de l'algèbre
– a. Literal calculation
Logarithme:
nombre
y tel que ay = x, a est la base.
Si a = e, le logarithme est dit
népérien;
Si a = 10, le logarithme est décimal
– v. Logarithme népérien / Exponentielle
– a. Algorithm
La fonction logarithme de base 10 ou
logarithme décimal associe à tout réel x strictement positif, un réel noté log x. Elle
vérifie les propriétés: log 1 = 0; log 10 = 1; log 10n = n.log 10 =
n, pour tout entier naturel n.
En gros, elle compte la
quantité de chiffres dans un nombre.
Logiciel: ensemble des
instructions qui font fonctionner un ordinateur.
Proche de programmes ou ensembles de programme destiné à une application
particulière
– ex. Le logiciel de traitement de texte; Le logiciel de planification de
départ des avions dans un aéroport; etc.
– par opposion à matériel (hardware en anglais).
– v. Programmes
présents sur ces pages – Index ; Algorithme, informatique, matériel (ordinateur), historique de l'informatique
– a. Software
Logicisme: approche,
développée à l'origine par Gottlog Frege,
qui prétend que toutes les mathématiques sont réductibles à la logique.
– v. Logique
– a. Logicism
Logique: science du
raisonnement dans l'abstrait, peu importe à quoi cela s'applique; La logique est
la science qui permet d'établir des règles précises conduisant à un
raisonnement rigoureux.
– v. Algorithme,
logiciel, tiers exclu
– a. Logic
Logique de Boole ou algèbre de
Boole ou calcul booléen: logique "vrai / faux" ou "0 /
1"; logique dont les variables prennent deux valeurs qui s'excluent mutuellement.
– v. Logique de
Boole
– a. Boolean logic
Le calcul booléen utilise les techniques de
l'algèbre pour traiter des expressions à deux valeurs. Applications en
informatique et dans la conception des circuits électroniques (automates, ordinateurs).
Logistique**: En mathématique,
se réfère à l'évolution d'une population humaine ou animale.
– étym. du grec logistikos qui veut dire calcul. Terme proposé par Pierre
Verhulst en 1845 sans explication. Sans doute une proximité avec logarithme.
Deux termes synonymes à l'époque.
Loi logistique ou fonction logistique: modélisation continue de
l'évolution d'une population.
Loi particulière de probabilité.
– v. Croissance logistique, chaos
– a. Logistic distribution
Suite logistique: même chose en discret, d'une année sur l'autre par
exemple
– v. Loi logistique
En 1845, Pierre François Verhulst définit la
loi logistique en tant que modèle démographique, reprise en 1976 par le
biologiste Robert May. Allure de cette fonction polynomiale: xn+1 =
k · xn · (1 – xn). Son comportement est chaotique.
Loi: principe de base,
relation fondamentale.
En physique, formule qui modélise un phénomène, qui rend compte des
observations.
En maths, c'est un théorème applicable dans de nombreux cas.
– ex. La loi des grands
nombres, law of large numbers (LLN).
Loi des signes: lois applicables
aux opérations.
– ex. Le produit de deux nombres négatifs est positif.
– a. Calcul
arithmétique, priorités des
opérations
Loi de composition des fonctions (ou
des applications): pour tout couple d'applications f
et g de E dans E, leur composée f*g appartient à l'ensemble
des applications de E dans E.
– v. Loi de composition, vocabulaire des structures
algébriques
– a. Law of composition: rule that defines an operation.
Synonym of operation on a set E, when E is closed under the operation.
Loi de composition interne (sur un
ensemble): l'addition
et la multiplication
sont des lois de composition interne; ce terme vise à la généralisation à
d'autres opérations; c'est l'application de E x E dans E; notée par un rond
dans ![]()
– syn. Opération
– v. Types
de lois de composition
– a. Internal composition law, groupe, Cayley (table)
Loi de composition externe (sur un
ensemble): action d'un ensemble
sur un autre; application de ![]()
– a. External composition law
The
composition law is internal if the application that defines it maintains the
same set, both in the starting pair of sets and in the arrival pair . If the
starting sets are different from each other, the composition law is said to be
external.
Loi de probabilité: application
associant à chaque élément d'un ensemble d'évènements une probabilité
déterminée.
– a. Probability distribution: mathematical function that gives the
probabilities of occurrence of different possible outcomes for an experiment.
Loi gaussienne: v. Gauss
Lois de De Morgan: en logique, relation
symétrique entre une proposition
et sa négation.
– a. De Motgan's laws
Elle logique classique:
non (A ou B) = non A et non
B
non (A et B) = non A ou non
B
En logique propositionnelle:
![]()
![]()
En
théorie des ensembles:
![]()
![]()
Loi horaire: en mécanique,
fonction scalaire du temps, décrivant le déplacement du
point P selon le mouvement considéré.
– v. Énigmes
avec la vitesse
Longitude:
coordonnée
géographique ouest-est; angle entre le méridien du lieu
et celui de Greenwich (Angleterre).
– ex. Paris est située à un peu plus de 2° Est
– v. Sphère terrestre, latitude, GPS,
GMT
– a. Longitude
Longueur: en général,
distance entre deux points.
Et en particulier: plus grande dimension du rectangle, la plus
petite étant la largeur; on ajoutera la hauteur pour un
parallélépipède.
Ces trois grandeurs, longueur, largeur et hauteur, sont toutes des
longueurs au sens général.
– a. Length, width, breadth, depth, range
Losange:
quadrilatère dont
les quatre côtés ont même longueur.
Ses diagonales sont perpendiculaires;
– vieux nom: rhombe;
losange en espagnol: rombo.
– v. Losange, carré
– a. Rhombus: all four sides are equal in length, and both pairs of opposite
sides are parallel.
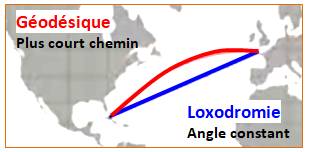 Loxodromie: ligne droite entre deux points sur une carte Mercator. Courbe
qui coupe les méridiens d’une sphère sous un angle
constant.
Loxodromie: ligne droite entre deux points sur une carte Mercator. Courbe
qui coupe les méridiens d’une sphère sous un angle
constant.
– v. Géodésique
– a. Rhumb line
Lunule (d'Hippocrate): sorte de quartier
de lune accrochée au côté
d'un triangle rectangle
ABC, BC étant l'hypoténuse;
on dessine les trois cercles de diamètre BC, AB et AC extérieurs au triangle.
Les deux lunules ainsi crées ont une aire égale à celle du triangle.
– v. Calcul de l'aire de la lunule.
– a. Lunula
Lyapounov
(fonction de -)**: fonction qui, à partir d'une équation
différentielle, permet d'estimer la stabilité d'un point d'équilibre ou, plus
généralement, d'un mouvement (c'est-à-dire d'une solution maximale).
– v. Fonction de Lyapounov, résolution avec
IA
– a. Lyapunov
functions
En
2024, Meta AI (ex Facebook) a résolu un problème de math vieux de 135 ans concernant
les fonctions de Lyapunov. Fonctions qui sont essentielles pour l'analyse de la
stabilité des systèmes dans le temps. Elles permettent de prédire le
comportement dynamique de systèmes. On pense au problème des trois
corps, par exemple.
![]()
|
Voir |
|
|
Aussi |
|
|
Autres |
|
|
Cette page |
![]()