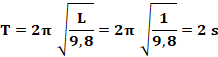Dictionnaire de base des mathématiques: jargon démystifié

Comme tout domaine, les mathématiques recourent à un vocabulaire propre, un jargon. Certains mots, proches ou non de mots du langage courant, n'entrent pas tout de suite dans notre conscience. Mais, une fois le "déclic" réalisé (le "Ah, Ah" dirait Gardner), le mot devient soudain familier.

Un exemple classique en physique: définir l'entropie par une équation ne dit absolument rien. Dès que l'on propose de traduire ce mot par "désordre " ou "bordel ambiant", alors le paysage s'éclaire.

Les définitions rapides des mots ne s'embarrassent pas des nuances. Se reporter au lien pour des explications détaillées.

NB: En mathématique, il existe un vocabulaire précis et certains sont pointilleux quant à leur emploi. Si vous êtes élève, remettez-vous en aux consignes de vos professeurs. Cette page a pour seul but de démystifier ces mots, le plus simplement possible.

Voir Enseignement – Index

Jargon de l'école
*Adjacent*	Collé à côté; qui ont un côté en commun.
*Aire*	Surface ou superficie	>>>
*Algorithme*	Recette de calcul; description pas à pas d'une méthode pour obtenir quelque chose.	>>>
*Circonférence*	Le tour du cercle, son périmètre	>>>
*Coordonnées*	Nombres qui définissent un point. Analogie avec la définition d'une case dans une grille.	>>>
*Plan*	Analogie avec une feuille de papier (deux dimensions). Par opposition à l'espace (trois dimensions)	>>>
*Quotient*	Résultats de la division. Exemple: 5 est le quotient de la division 10 / 2.	>>>
*Somme / Différence*	Résultat de l'addition et de la soustraction.	>>>

Suite Vocabulaire de base des mathématiques

Jargon du collège
*Affine*	Qui évolue de façon proportionnelle, linéaire.	>>>
*Aléatoire*	Au hasard	>>>
*Champ*	Caractérise la propriété en chaque point d'un plan ou d'un espace Comme le champ magnétique dont l'intensité et la direction varie en tout point.	>>>
*Ensemble*	Collection de choses, d'éléments.	>>>
*Homothétie*	Transformation qui grossit une figure (ou l'inverse). Le rapport d'homothétie précise le facteur de grossissement. Homothétiques: qui sont semblables	>>>
*Isométriques*	Qui ont même mesure, même longueur; qui sont égaux	>>>
*Orthogonal*	Perpendiculaire.	>>>
*Scalaire*	Un nombre normal. Utilisé dans le monde des vecteurs.	>>>
*Symétrie*	Effet miroir qui produit une image inversée de l'original.	>>>
*Théorème*	Propriété démontrée une fois pour toute. Le lemme est un "petit" théorème souvent provisoire.	>>>
*Translation*	Glissement sans faire tourner	>>>
*Trigonométrie*	Calculs dans les triangles: côtés et angles	>>>

Suite en DicoMot Math

Jargon du lycée
*Isobarycentre*	Centre de gravité Pour un objet mathématique ou un objet physique homogène (centre de masse)	>>>
*Complexe*	Un tout formé de deux nombres: un réel et un imaginaire Le couple représente les coordonnées d'un point du plan.	>>>
*Déterminant*	Somme de produit dans le calcul des matrices	>>>
*Discret*	Contraire de continu Valeur qui progresse par bonds	>>>
*Discriminant*	Terme général pour la résolution des équations Sa valeur détermine la nature des racines	>>>
*Ensemble quotient*	On pourrait dire ensemble partagé selon les restes de la division	>>>
*Groupe*	Ensemble d'éléments considéré comme un tout. Un objet mathématique qui possède des propriétés particulières.	>>>
*Imaginaire*	Nombre annoncé par le nombre i tel que i² = –1	>>>
*Isomorphisme*	Correspondance un à un entre deux ensembles.	>>>
*Matrice*	Tableau de nombres considéré comme un tout.	>>>
*Norme*	Longueur d'un vecteur.	>>>
*Tenseur*	Une généralisation des vecteurs.	>>>
*Vecteur*	Une flèche représentant un déplacement ou une force	>>>

Suite en DicoMot Math

>>> Lettres de l'alphabet

Langage du calcul

Mots usuels du calcul
*Calculer*	Effectuer des opérations simples (adition, soustraction, multiplication, division) ou élaborées (puissance, racine, sinus …). Calculer une expression se dit mais n'est pas conseillé. Il existe des termes plus précis, comme: simplifier, réduire, développer, factoriser.	Calculer: 12 x 11. C'est: 132. Calculer le prix de 10 kg de carottes à 1,50 euro le kilo: 10 x 1,50 = 15 euros. Calculer E = 10x + 5 avec x = 2. On remplace x par 2: 10x 2 + 5 = 25 Voir Initiation aux calculs
*Simplifier*	Effectuer tous les calculs possibles pour éliminer le superflu, l'inutile. Rendre plus lisible, mais attention aux notations ambigües: Correct: a × b = a·b = ab Ambigüe : 6 ÷ 2 (1 + 2) = ? En algèbre la croix pour multiplier est remplacée par un point ou rien, cela pour réserver la lettre x à la notation de l'inconnue.	Simplifier l'écriture 3 × a × b s'écrit 3ab a × a × a se simplifie en a³ Simplifier une expression arithmétique 10 + 2×3 + 2² = 20 Simplifier une expression algébrique 3x – (2x + 5) = x – 5 Simplifier une fraction
*Réduire*	Réduire expression algébrique consiste à simplifier une expression en regroupant les termes de même nature. Puis, effectuer tous les calculs possibles (encore simplifier). Dans certains cas, il sera nécessaire de développer et factoriser pour obtenir une expression algébrique plus compacte. Note: dans l'exemple, on remarque immédiatement que E = 0 pour x = – 1/3. Il suffit de substituer x par – 1/3.	Réduire 2x² + x + x² = 3x² + x Pour plus de lisibilité les termes sont ordonnés 3x + 2x² + x³ = x³ + 2x² + 3x ab + a² + b² + a²b = a² + a²b + ab + b² Réduire avec développement et factorisation E = (9x+2)(x+1) – 5x – 1 E = 9x² + 11x + 2 – 5x – 1 E = 9x² + 6x + 1 E = (3x + 1)²
	Réduire des fractions au même dénominateur.
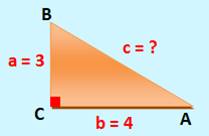
*Appliquer*	Appliquer un théorème, une règle, une procédure, un algorithme Utiliser une loi connue pour conduire un raisonnement, une démonstration.	En appliquant la commutativité: a · b = b · a En appliquant le théorème de Pythagore: a² + b² = c²

APPLIQUER: exemple de rédaction

Problème

Trouver la longueur de l'hypoténuse AB du triangle rectangle ABC.

Solution

Le théorème de Pythagore énonce que: dans tout triangle rectangle: a² + b² = c².

Or, le triangle ABC est rectangle, on lui applique le théorème de Pythagore en substituant les longueurs connues par leur valeur numérique:
c² = a² + b² = 3² + 4² = 25 = 5²

Le résultat étant la valeur de c², la valeur cherchée est sa racine carrée: c = 5.

Le triangle isiaque

Voir Propriétés de ce triangle

On aurait pu dire: on utilise le théorème de Pythagore en remplaçant les lettres par leur valeur numérique.

Résoudre

Résoudre c'est trouver la solution à un problème.

Par exemple, calculer les racines d'une équation, découvrir le fin mot d'une énigme, …

Résoudre un triangle: à partir de quelques paramètres, trouver les autres.

Le verbe solutionner a le même sens, mais est plutôt familier.

Résoudre cette équation:

3x = 12

Solution: x = 12/3 = 4

Substituer

Remplacer un élément par un autre, généralement une lettre par un nombre, une inconnue par sa valeur.

Alors que remplacer s'applique à n'importe quoi, substituer s'applique à des éléments de même nature: le premier est général (une longueur), le second est particulier (un nombre). En informatique, on dit instancier.

Exemples: remplacer les variables par des valeurs numériques; inverser le rôle des variables; réintégrer la valeur complète d'une variable intermédiaire, etc.

Note: il est conseillé de réduire une expression avant de substituer les valeurs numériques aux variables.

En substituant x par 2, on a:

Que devient y = x² + 2 en substituant x par z + 1:
y = (z + 1)² + 2 = z² + 2z + 1 + 3

Substituer

(le nombre d'or) dans

On obtient:

Application numérique

En maths comme en science, les calculs se font sous forme littérale pour conserver une loi générale.

L'application numérique consiste à substituer les lettres symboliques par des nombres pour connaitre les valeurs dans des cas particuliers.

Périmètre du cercle de rayon 5 m ?

Période du pendule de longueur 1m ?

Transformation des expressions algébriques (on dit aussi: des expressions littérales)
*Développer*	Développer une expression algébrique, c'est transformer un produit en somme. En gros: "déplier" une expression avec parenthèses. En anglais, on dit: to expand.	Développer Puis réduire (ou simplifier)
*Factoriser*	Factoriser une expression algébrique, c'est transformer une somme en produit (inverse de développer). C'est mettre en commun des facteurs. L'idée est de trouver les racines, les valeurs qui rendent le polynôme nul.	Factorisation avec des nombres 10a + 5b = 5 (2a + b) Factorisation algébrique simple Identité remarquable Polynôme nul pour x = 2 ou x = –2 Factorisation élaborée
	Factoriser un nombre: trouver les facteurs du nombre (les plus petits diviseurs).

Voir Bases de l'algèbre (réduire, développer et factoriser)

Suite	Voir Haut de page (ou double-clic) Divers termes de maths Caractères spéciaux
Voir	Atlas des maths – des références Débutants – pour juniors ou novices Enseignement – Index Notes de musique
Aussi	DicoNombre – tous les nombres de 0 à l'infini DicoLettre – signification des lettres en maths et ailleurs
Autres	Voir page des liens et références
Cette page	http://villemin.gerard.free.fr/Referenc/Encyclop/Jargon.htm