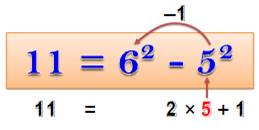|
||||||||||||||||||||||||||||||||
![]()
|
|
|
Si vous achetez
moins de dix roses pour votre amie, choisissez un nombre impair. Pourquoi? Eh bien, dans le temps, seuls
les fleuristes les vendaient par quantité impaire, alors que sur le marché,
elles se vendaient en quantité paire. |
|
Chez le
coiffeur: la raie au milieu? Pas facile, m'sieur vous avez un nombre impair
de cheveux ! |
|
Eunuque: homme
hors-pair – D'après Légitimus. |
|
Numero deus
impare gaudet. Traduction: le nombre impair plaît au dieu. Erreur de traduction: le nombre deux se
réjouit d'être impair. |
Rimes paires à-peu-près
|
0 – Zorro, braséro,
trois_héros 2 – Hideux, dieu,
adieu, pardieu, 4 – Pancarte,
psychiatre 6 – Abscisse, saucisse,
narcisse, il s'hisse |
8 – Fuite, poursuite, Inuit 10 – Indice, jadis,
préjudice, immondice, appendice, drisse, tisse 12 – Partouze,
ventouse, bouse, barbouze. |
Voir
Pensées & humour
/ Poésie
|
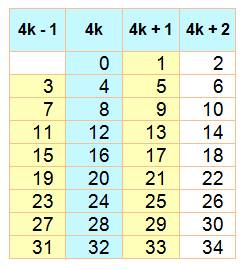
NOMBRES PAIRS & IMPAIRS Nombres
divisibles par 2 (PAIR) ou non (IMPAIR).
Mis en rang par deux les élèves forment un nombre exact de couples (le nombre
est pair) ou il reste un élève isolé
(nombre impair). Il est utile de connaître la traduction en anglais, car un nombre
pair est souvent représenté par la lettre E et impair pair par O – Cela pour
ne pas confondre avec p de premier et i de imaginaire.
Mnémotechnique: ODD
est le symbole de l'impair avec D
en double et un O en plus. Un autre truc: ODD s'écrit avec un nombre
impair de lettres.
|
Voir Découverte des nombres impairs
avec une énigme simple
|
Yeux
pers: entre bleu et le vert, le bleu étant
dominant, le vert pouvant tourner au violet voire au noir. Couleur qui n'est pratiquement utilisée
que pour les yeux. Se prononce comme pair. |
|
–
Caractérisation |
|
|
|
|
|
Autre exemple: 101 = 2 x 50 + 1 = 51 + 50 = 51² –
50² Amusement Somme des chiffres impairs: 1 + 3 + 5 + 7 + 9 = 25 Somme des chiffres pairs: 2 + 4 + 6 + 8 = 20 Égalité entre les impairs d'un côté et les pairs
de l'autre:
|
|
Voir Modulo
2 / Nombre
84,333… / Pannumériques
Pagination
des livres: pages paires à gauche et impaires à droite

|
|
||
|
|
|
|
|
Ils sont tous égaux
à: |
Ils sont tous égaux
à: |
|
|
|
|
|
|
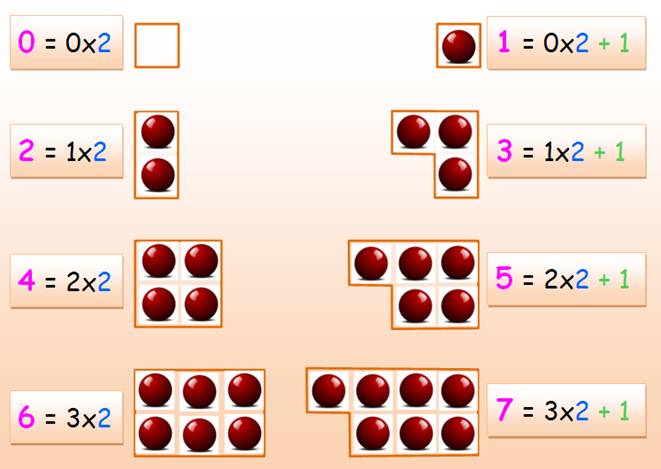
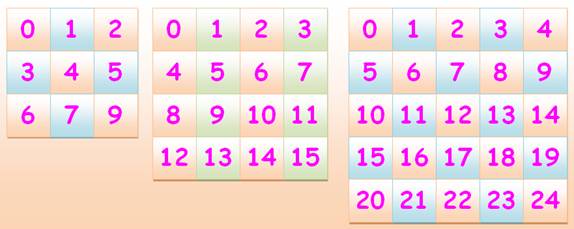
Illustration Avec
une quantité impaire de colonnes, on forme
un damier avec les nombres de même parité en quinconce;
et, avec une quantité paire, un alignement
vertical des nombres de même parité.
|
||
Voir Modulo
|
|
Liens vers la page de développement |
|
|||
|
3² – 2² 4² – 3² 5² –
4² |
= 5 = 7 = 9 |
= 3 + 2 = 4 + 3 = 5 + 4 |
Impairs
&
différence de carrés & somme de
consécutifs |
|
|
2 2 + 4 2 + 4 + 6 |
= 2 = 6 = 12 |
= 1 x 2 = 2 x 3 = 3 x 4 |
Somme
des pairs |
|
|
1² = 1 2² = 1 + 3 3² = 1 + 3 + 5 4²
= 1 + 3 + 5 + 7 |
Somme
des impairs |
|||
|
1 + 3 + 5 = 3 2 7 +
9 + 11 = 3 3 |
Nombres
impairs, carrés et cubes |
|||
|
|
||||
|
3 x
5 = 4² – 1 4 x
6 = 5² – 1 |
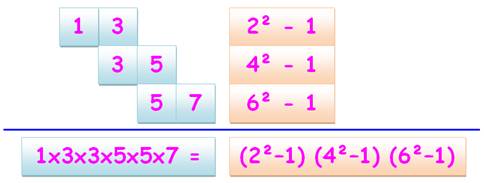
Produit
des pairs et des impairs Fraction
de ces produits (Wallis) |
|||
|
|
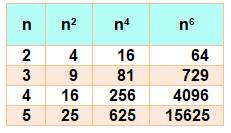
Un
nombre, son carré, sa puissance quatrième et toutes les puissances en 2k sont
de même parité. |
|||
Devinette double et une en bonus
|
Devinette
pour s'échauffer: j'ai une pièce de 1€ dans une main et de 2€ dans l'autre.
Comment faire, avec un petit calcul simple, pour deviner où sont chacune des
pièces? Réponse >>> Plus
coriace: j'ai dans une de mes mains un nombre pair de cailloux et dans
l'autre main un nombre impair. Dans quelle main ai-je le nombre pair de
cailloux ? Pour deviner, tu me poses une seule question dont la réponse doit
être un nombre. Quelle est la question? Réponse
>>> |
|
Pour matheux:
si a + b et ab sont deux nombres pairs, prouvez
que a et b sont pairs. Réponse >>> |
Voir Magie
|
|
||
|
4 x 6 = 24 = 25 – 1 = 5² – 1 Le produit de deux nombres pairs consécutifs ou de deux nombres impairs
consécutifs (tout couple de nombres avec un écart de 2) est égal au carré du
nombre moyen moins un.
|
1 x 3 = 2² –
1 2 x 4 = 3² –
1 3 x 5 = 4² –
1 4 x 6 = 5² –
1 5 x 7 = 6² –
1 … (a – 1)(a +
1) = a² – 1 1 x 5 = 3² –
4 2 x 6 = 4² –
4 3 x 7 = 5² – 4 4 x 8 = 6² – 4 5 x 9 = 7² – 4 … (a – 2)(a + 2) = a² – 4 |
|
|
Suite en produits de
Wallis |
||
Voir Consécutifs
/ Proniques / Divisibilité des carrés
impairs moins 1
|
|
||
|
Fraction
avec les impairs consécutifs, autant en haut et en bas. |
|
|
|
Démonstration |
|
|
|
1 + 3 + 5 + … +
(2n – 1) = n² |
||
|
(2n + 1) + (2n +
3) + … + (4n – 1) = n . 2n + 1 + 3
+ … + (2n – 1) = 2n² + n² = 3n² |
||
|
Fraction |
n² / 3n² = 1/3 |
|
Voir Nombre
0,333…
|
|
||
|
Inverse de deux pairs consécutifs. Les deux nombres de la fraction résultat sont les deux composantes d'un triplet de Pythagore. |
3² + 4² = 5² |
|
|
Démonstration |
|
|
|
Somme des fractions |
|
|
|
Somme des carrés du numérateur et du dénominateur |
(2k + 1)² + (2k
(k + 1))² |
|
|
|
|||
|
SOMME |
PAIRS |
IMPAIRS |
|
|
|
30 2550 250 500 25 005 000 |
25 = 5² 2500 = 50² 250 000 = 500² 25 000 000 = 5000² |
|
|
Somme alternée (Pairs – impairs) |
|||
|
|
5 = 10/2 50 = 100/2 |
||
|
PRODUIT |
PAIRS |
IMPAIRS |
|
|
|
3 840 0,34…1080 = 3424322470 2511976248 2464328952 0818597511 8675053719 1988279156
5446348800 0000000000 |
945 0,27 1079 = 272539213 9750729502 9807132454 0091863329 0796330545 8034137343
2882344310 6201171875 |
|
Voir Somme
des pairs / Somme des impairs / Factorielle
Que faut-il faire dans la vie ?
|
Persévère! |
Voir Jeux
de mots / Rébus
|
Numero deus impare
gaudet. Un chiffre impair
plaît aux Dieux. Virgile, Les Bucoliques |
|
|
Voir Pensées & humour
|
|
||
|
|
||
|
Exemple 1
|
a = 3b Si b est pair, alors a = 3 (2k) = 6k
qui est pair Si b est impair, alors a = 3 (2k + 1) =
6k + 3 qui est impair. |
|
|
Exemple 2
|
q
= a3 – 9ab s
= 3a2b – 3b3 Premier cas: a et b sont pairs avec
la méthode des pairs (2k) / impairs (2k+1): q = (2k)3 – 9
(2k)(2k') = 8K –
9 . 4K' s = 3(2k)2
(2k') – 3(2k')3 = 3.8K – 3.8K' Second cas: a et b sont impairs avec
la méthode des restes de la division par 2 (modulo) q = (2k+1)3 –
9 (2k+1)(2k'+1) s
= 3(2k+1)2 (2k'+1) – 3(2k'+1)3 Conclusion Si
a et b sont de même parité, s et q sont tous les deux pairs. Ce qui est
incompatible avec notre hypothèse. Alors, a et b sont de parités opposées. |
|
Fractions qui produisent les nombres pairs
et impairs
|
Nombres pairs, suivis des nombres
impairs |
|
|
Nombres impairs, suivis des nombres
pairs |
|
Voir Autres fractions particulières
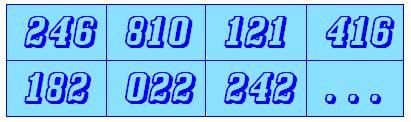
Réponse: 628 – Suite des
nombres pairs dont les chiffres sont groupés par trois.
![]()
![]()
|
Suite |
|
|
Nombres géométriques |
|
|
Voir |
|
|
Diconombre |
|
|
Cette page |
![]()
|
Tu
donnes à ton copain ou copine une pièce de 1€ et une de 2€. Il doit les
cacher chacune dans une main et tu paries que tu vas deviner où sont les
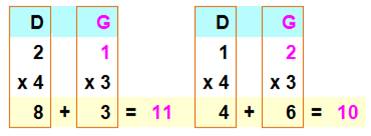
pièces grâce à un petit calcul. Tu
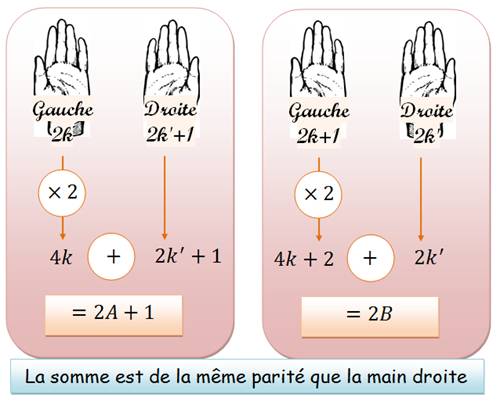
lui demandes de faire 4 fois la main droite plus 3 fois la gauche. Si
le résultat qu'il te communique est impair, la pièce de 1€ est dans la main
gauche.
En
fait, le résultat sera de la même parité que celle de la pièce placée dans la
main gauche. Pour
ne pas recommencer le même tour à chaque fois tu peux remplacer 4 par un
autre nombre pair et 3 par un autre impair. Multiplier
la quantité de cailloux dans sa main droite par 2 et ajouter ceux de la main
gauche. Si la somme est paire, le nombre pair est dans sa main gauche. Variante pour masquer un peu plus les choses Multiplier
la quantité de cailloux dans sa main droite par un nombre pair, celle de sa
main gauche par un nombre impair, et faire la somme. Si elle est paire, le
nombre pair est dans sa main gauche. Explication La
multiplication par un nombre pair à gauche laisse le produit pair, alors que
la multiplication par un impair à droite donne un produit de la même parité
que celle du nombre multiplié. Voir Multiplication
|
|
Question Si a + b et ab sont
deux nombres Pairs, prouvez que a et b sont Pairs. Solution Il suffit de chercher
les Impairs avec a + 1 et b + 1. (a + 1)(b + 1) = ab
+ (a + b) + 1 = Pair + Pair + 1 = Impair Or, un Impair ne peut
pas avoir de facteur Pair. C'est que a + 1 comme
b + 1 sont chacun Impairs. Donc a et b sont
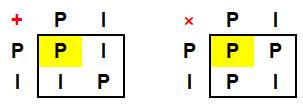
Pairs. Autre manière avec tables de vérité La table d'addition
et celle de multiplication montrent qu'un résultat pair dans les deux cas
n'est réalisé seulement qu'avec deux nombres pairs.
|
![]()