![]()
|
|
Ce site est désormais accessible en |
|
22 Novembre 2025
![]()
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Complètement rond, ce type commençait à lui taper sur le
système. Ni une, ni deux,
il lui a mis la tête au carré! |
Siège d'Apple à
Cupertino (Californie) |
|
Et le cercle vicieux, avec quel type de compas tu le
construis? |
Voir Pensées & humour

Index des courbes particulières et solides
associés
|
Courbes fermées, convexes et avec axe de symétrie |
|
Courbes |
||
|
Autres |
Autres |
|||
|
|
||||
|
|
Sinus … |
|||
|
|
||||
|
|
|
|||
|
|
|
|||
|
Ellipsoïde |
Ovoïde |
|||
|
|
|
|||
|
|
|
|
|
|
![]()
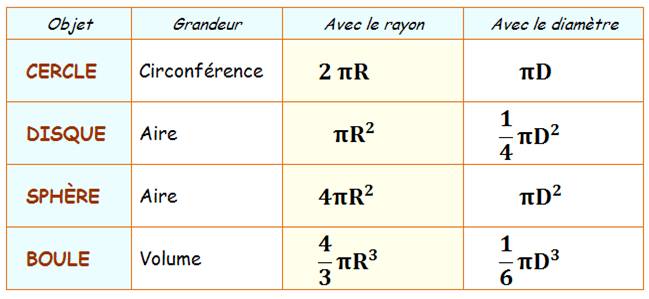
Mémento utile (on retient plutôt les formules avec le rayon)
Mnémonique
pour périmètre et aire: deux pierres et pierres
deux (+ l'aire fait intervenir un carré, bien sûr)
Il est amusant de constater qu'avec la surface
de quatre disques on couvre la surface de la sphère de même rayon.
|
|
TOUS
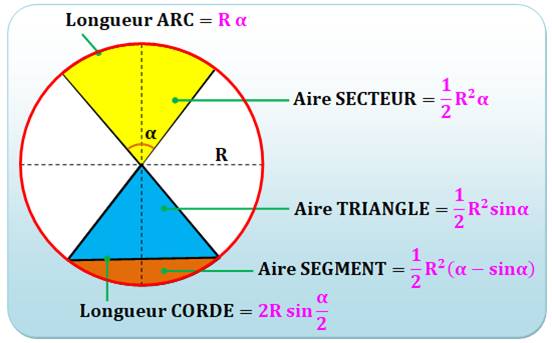
les angles sont en RADIANS (π
= 180°) En
mathématiques, sans précision, les angles sont en radians. |
Voir Aires
secteur, segment … / Arc,
corde, sagitta / Angles en
radians
![]()
|
Figure de la révolution en quatre
lettres? Rond |
Définition de mots croisés |
|
Un cercle
d'amis est un très petit cercle. |
|
|
Le monde est rond. Qui ne sait nager va au fond. |
Proverbe du XVIe Note: Depuis, en
1999, on a montré que le monde (l'univers) est plat
et…infini |
|
Prenez un cercle Caressez-le : il devient
vicieux. |
Eugène Ionesco - La cantatrice chauve |
|
L'univers est
un cercle dont le centre est partout et
la périphérie nulle part. |
|
|
Il tourne dans le cercle étroit de ses plaisirs, comme un jeune
chat jouant avec sa queue. |
Goethe – Faust |
Voir Expression avec le mot
"cercle"
![]()
|
|
DISQUE
|
Circonférence en anglais: girth
|
Pourquoi les
bouches d'égout sont-elles rondes? C'est la seule forme dont le couvercle ne
passe pas par la bouche. Avec une forme carrée, il suffit de présenter le
couvercle selon la diagonale du trou. |
|
Voir Pensées
& humour / Puzzles
|
|
||
|
|
|
|
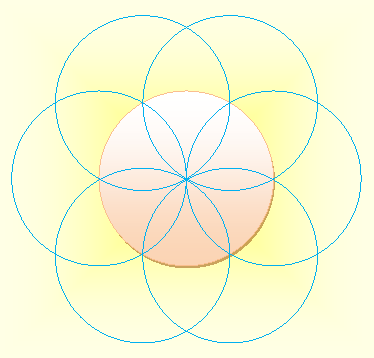
Voir Nombre six / Fractions dans le cercle/ Partage du cercle / Rosace
Cas du partage du cercle central en 12, formation d'une rosace

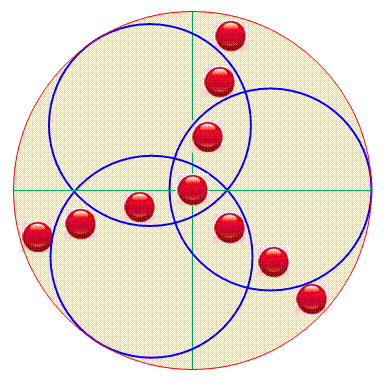
Énigme: comment encercler dix pions avec trois cercles?
|
Un cercle et dix pions disposés en Y.
Comment, avec trois cercles, isoler chacun des pions. Énigme parfois habillée de la manière
suivante: un enclos circulaire et dix chèvres, comment les isoler avec trois
enclos circulaires? On vérifie bien que les 10 billes sont
dans chacune des 10 régions. |
Voir Jeux
et énigmes
Merci à
Romuald Perrot
|
|
|
|
Classiques
Euclide
Définition
mathématique
Autres
|
|
|
|
|||
|
|
Il est extraordinaire
d'avoir le même rapport:
|
||
Suite en Propriétés / Aire du cercle / Méthode
d'Archimède
|
À gauche, effet surprenant ! La
longueur du rectangle bleu est égale au périmètre du cercle. À droite, paradoxe du
verre: la hauteur de ce grand verre est inférieure au périmètre du cercle du
haut comme celui du bas. h = 0,8 périmètre du cercle du bas et h = 0,6 celui du cercle du haut.
|
|
|
|
|
|
|
Suite imagée en Vocabulaire
du cercle
Voir DicoMot / Objets de base de la géométrie
|
|
||
|
Il est facile de construire un cercle pas à pas en
suivant le type d'instruction que l'on trouve dans le langage LOGO. 1) Faire un pas en avant. 2) Tourner à droite de n degrés. 3) Recommencer 1) et 2) en vous arrêtant si vous vous retrouvez sur le
dessin déjà construit.
|
1)
2) n) |
|
|
Fin) Cercle complet
|
||
Voir Programmation du dessin du cercle / Programmation / Programmation récursive
Construction du cercle sans le
centre
|
|
|||
|
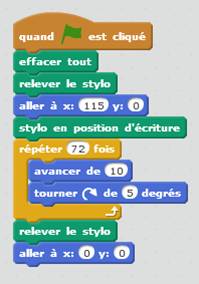
Programme
|
Commentaire Le programme démarre en cliquant sur le drapeau vert. On efface la zone de dessin. On relève le stylo pour rejoindre un point du futur cercle
(complètement à droite). Stylo en position de tracé. Boucle qui répète 72 fois (72 x 5 = 360°)
En fin de toutes ces 72 étapes, on se dirige au centre du cercle sans
écrire. |
Résultat
de l'exécution
Choisir
le lutin crayon, ou laisser simplement le chat d'origine. |
|
Voir Programmer avec
Scratch / Programmation
de l'icosagone
|
|
||
|
Français
|
|
|
|
Anglais
|
Espagnol
Allemand
|
|
|
|
|
|
|
|
Voir Chirurgie
|
Toute
chose faite par un Indien est faite dans un cercle,
et il en est ainsi parce que le Pouvoir de l'Univers
agit toujours moyennant des cercles, et
toute chose tend à être ronde (…) J'ai
entendu que la Terre est ronde comme
une boule, et les étoiles
elles aussi sont rondes. Nos
tentes étaient circulaires comme les nids
des oiseaux, et elles étaient toujours disposées en cercle.
|
Hehaka Sapa, ou Black Elk, indien Oglala,
branche des Dakotas (Sioux)
Source: Indiens – Marie-Hélène
Fraïssé – Chêne – 2011 & Message d'Indiens
|
|
|
|
Chariots
romains Les
chariots romains possédaient des roues mais n'étaient pas équipés de système
de direction. La prise de virage était problématique.
Le
currus était plus ancien et ne pouvait transporter que deux personnes. Avec
deux chevaux, il s'agissait d'un biga; avec trois, un triga et avec quatre,
un quadriga. Les roues, cerclées de fer, étaient amovibles pour faciliter le
rangement. Source de l'illustration: A
roman military wagon, laden with armour and weapons |
|
Voir Terre
/ Lune / Arc-en-ciel / Tournesol
/ Homme de Vitruve / Seins / Œil
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()
Exemple de
calcul en ligne
Avec The Complete Circular Arc Calculator – handymath.com - Calculateur en ligne

Renvois de liens suite à refonte des pages sur le cercle