|
Édition du: 20/12/2023 |
|
INDEX lettre G |
Dictionnaire de base du vocabulaire des mathématiques |
|
|
Faites
un double-clic pour un retour en haut de
page
Pour
trouver un mot: Ctrl F et tapez le mot
cherché
|
Avertissement Dictionnaire pour débutants,
juniors, novices, "nuls" … !!! On privilégie la compréhension par rapport à une rigueur mathématique !!! Les liens permettent de compléter et d'approfondir Pour une version
plus académique se reporter aux ouvrages spécialisés |
Légende Parfois,
plusieurs définitions sont données: de la plus "intuitive" à la
plus correcte mathématiquement Mode de recherche: si vous ne trouvez
pas symétrie centrale à symétrie, voyez à centrale, par exemple. Difficulté: * notion avancée;
** notion complexe. |
Galois (groupe de - ): groupe
impliqué dans la caractérisation des symétries des
racines de polynômes.
Soit K un corps et L une extension de K. On appelle groupe de Galois de L sur
K, noté Gal(L/K) l'ensemble des automorphismes de L
laissant K invariant. Il s'agit d'un groupe pour la loi de composition des
applications.
– v. Groupe de Galois
Corps fini ou corps de Galois**: famille de polynômes en quantité finie
via les congruences.
Manière de passer du monde infini des polynômes à un monde fini.
– ex. avec le premier degré, il n'existe
que deux polynômes: x et x + 1.
– v. Corps de Galois, polynômes irréductibles
– a. Galois field (GF)
Gamme (musicale): ensemble de notes
rangées dans une octave.
Les gammes
occidentales comprennent sept notes.
– ex. La gamme de do majeur, monter ou descendre la gamme.
Pour y trouver l'octave (division par 2), la quinte
(par 3) et la quarte (par 4), il faut diviser la
gamme par le PPCM
de ces trois nombres, soit 12.
Toutes les gammes occidentales sont composées de douze demi-tons.
– ex. Comptez le nombre de touches blanches et noires entre deux notes DO sur
le piano: il y en a 12.
– v. Notes de
musique et gamme
– a. Scale (music)
Gamme majeure: cinq tons et de deux
demi-tons (5x2 + 2 = 12).
Gamme mineure: trois tons, d'un
ton et demi et de trois demi-tons (3x2 + 2x1,5 + 3 = 12).
– v. Fréquence, tierce
Gauche (surface -): surface
non plane; surface courbe dans l'espace.
Les sommets d'un polygone gauche n'appartiennent pas tous au même plan.
Une hélice, par exemple, est une courbe gauche.
Un quadrilatère gauche est un quadrilatère dont les quatre sommets ne sont pas
situés dans un même plan.
– a. Skew polygon, skew quadrilateral
Terme ou membre de gauche
– a. Left end side (lhs)
Gauss
(courbe de-) ou gaussienne* courbe dite en cloche qui représente la probabilité
la plus classique, la fonction gaussienne.
Densité de probabilité d'une variable aléatoire normale
réduite.
– v. Gaussienne
– a. Gaussian function
Loi gaussienne* loi
de répartition statistique dont la représentation est une courbe en cloche, qui
décroît exponentiellement
vite de part et d'autre de la moyenne.
– v. Distribution, brownien
– a. Gaussian function
Gauss (théorème de – ou lemme de
-): a et b deux nombres premiers entre eux, si a divise b.c,, alors il divise
c.
– notation: Si a | bc et PGCD (a, b) = 1, alors a | c.
Généralisation du lemme d'Euclide.
– v. Divisibilité, sa
démonstation
– a. Euclid's lemma
Gaussien (bruit -): par exemple: en
électronique, caractéristique du bruit de fond des appareils électroniques, dû
à l'agitation des électrons.
– v. Mouvement
brownien
– a. Additive white Gaussian noise
Bruit blanc: la densité spectrale de
puissance est la même pour toutes les fréquences de la bande passante.
Le bruit additif blanc gaussien est un bruit blanc qui suit une loi normale de
moyenne et variance données.
GDC: graphic display
calculator: calculette avec résolution graphique.
Fonction disponible avec GeoGebra.
Exemple avec résolution de l'énigme
de la chèvre dans un champ rectangulaire.
Gendarmes (théorème des
-): la limite d'une fonction, encadrée par deux fonctions de même limite L, a pour limite L.
Exemple d'application avec ln(x)/x.
– autres noms: théorème de l'étau, théorème d'encadrement, théorème du
sandwich.
– a. Squeeze theorem, sandwich theorem
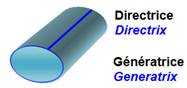Génératrice: par exemple, un
des segments
qui joint le sommet d'un cône à tous
point du disque de base.
Droite
qui s'enroule sur une courbe directrice pour engendrer un solide de révolution,
comme pour le cylindre ou le cône.
Une génératrice est une figure ou une ligne dont le déplacement engendre
une surface. Ces surfaces peuvent être par exemple des surfaces réglées ou de révolution
– v. Directrice, Réglée (surface -), axe de révolution
– v. Définition
générale du cylindre
– a. Generatrix or describent
Principales surfaces et leur génératrices
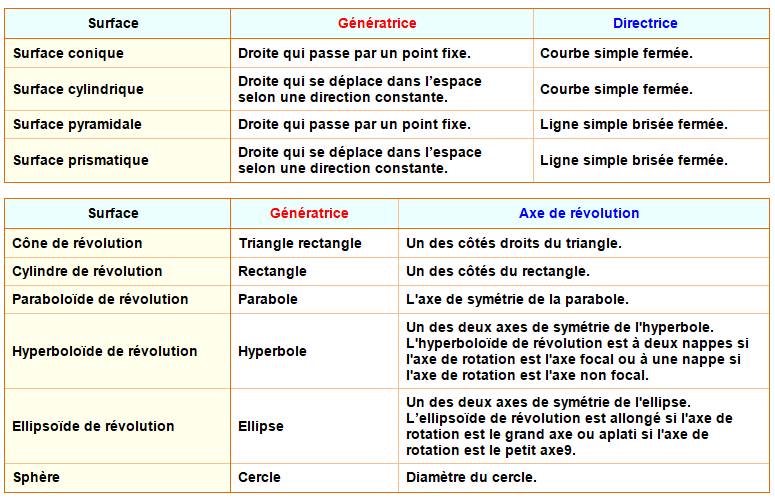
Source Génératrices
– Wikipédia
Génératrice (série ou
fonction -): fonction qui, développée, a pour coefficients les nombres d'une suite
donnée.
– ex. fonction génératrice
des nombres entiers: 1/(1 – x)² = 1
+ 2x + 3x² + 4x4 / Celle des nombres de
Catalan
– a. Generative function
OGF: fonction génératrice (ordinaire) ou (ordinary) generating function 
EGF: fonction génératrice exponentielle ou exponential generating function 
Genre
d'une courbe, d'une surface: nombre qui caractérise la quantité d'anses (ou de
trous) dans un objet géométrique.
Le genre d'une surface est le nombre maximum de courbes fermées simples
disjointes pouvant être tracées à l'intérieur de cette surface sans la
déconnecter.
– ex. La sphère est de genre 0; le tore, 2; la bouteille des Klein est de genre
2.
– a.
Genus of curve
Une courbe (objet à une dimension) dans un espace à n dimensions est
caractérisée par trois paramètres:
Dimension
de l'espace: D = 2, 3, 4 …
Degré de
la courbe: quantité de fois que la courbe traverse l'espace D – 1; et
Genre:
quantité de trous.
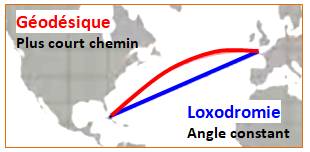Géodésique: Ligne (chemin)
donnant la distance
la plus courte sur une surface
non nécessairement plane; – ex. un arc de grand cercle
sur une sphère.
– v. Loxodromie, sphère terrestre.
– Illustration
avec une carte Mercator
(projection conforme).
– a. Geodesic
Géométrie: étude des
relations entre points, droites, cercles …
dans le plan (2D) ou dans l'espace (3D).
Science qui a pour objet l'étude des propriétés de figures, et la mesure de
leur étendue.
– étym. Mesure (metron) de la terre (gê).
Géométrie et éléments de base de la géométrie.
– a. Geometry
Géométrie analytique: faire de la
géométrie avec de l'algèbre,
des nombres, des équations.
Études géométriques à l'aide de nombres,
de coordonnées
relevées dans un repère
d'axes.
– a. Analytic geometry, coordinate geometry, Cartesian geometry
Géométrie euclidienne: celle de l'école.
– v. Géométrie
– a. Euclidean geometry geometry
Géométries non-euclidienne*: celle des surfaces
courbes.
– v. Les trois
géométries, topologie
– a. Non-Euclidean geometry
Géométrie de Lobatchevsky: construite sur
l'axiome que, par un point, on peut mener plusieurs parallèles à une droite
donnée. Tous les autres axiomes de la géométrie euclidienne sont conservés.
Géométrie riemannienne: généralisation de la géométrie à des espaces de k
dimensions.
Les espaces à géométrie hyperbolique sont vus comme des cas particuliers de
variétés riemanniennes "à courbure négative".
La géométrie riemannienne est une branche de
la géométrie différentielle qui introduit les concepts fondateurs de variété géométrique et de courbure.
Il s'agit de surfaces ou d'objets de plus grande dimension sur lesquels
existent des notions d'angle et de longueur, généralisant la géométrie
traditionnelle qui se limitait à l'espace euclidien.
Notion de formes (objets, images, …) proches basée sur une structure métrique adaptée.
Concepts élémentaires de géométrie riemannienne: variétés, métriques,
connections, géodésiques, distances induites et courbures.
Exemple du tore: il
existe deux manières de l’étudier : en tant que surface immergée dans l’espace
ambiant 
, ou comme quotient du plan 
par
l’action des translations entières. Plus simplement:on peut le
"construire" mentalement en collant les bords d'un rectangle, passant
ainsi de 3D à 2D. La géométrie riemannienne permet d’étudier la structure
métrique du tore
de façon plus pratique en seulement deux dimensions.
– a. Riemannian geometry is the branch of
differential geometry that studies Riemannian manifolds
Géométrie plane: on y traite des figures planes.
– a. Plane geometry
Géométrie dans l'espace: on y traite des
figures en trois dimensions (3D).
– a. Geometry of space
Géométrique (moyenne -): racine énième du produit de
n valeurs.
–
ex. Mg (5, 20) = √100 = 10
– v. Moyenne géométrique
– a. Geometric mean: the nth root of the product of n numbers.
Géométrique (suite ou
progression): suite de nombres dont chacun est égal au précédent multiplié par une
constante appelée la raison.
– ex.
10, 100, 1000, 10 000 …
– v. Progression
géométrique
– a. Geometric progression, geometric sequence
Géométrique (nombre -) ou
nombres figurés: nombre qui, représenté par des pions, permet de
construire une figure géométrique.
– ex. Nombres triangles,
carrés,
cubes, pentagonaux,
etc.
– v. Nombres géométriques.
– a. Figurate
number
Géométrique fractale: la géométrie
classique (euclidienne) traite de surfaces lisses, sans arêtes. La géométrie
fractale est toute autre: il y a des "cassures" à toutes les
échelles.
– v. Fractales
– a. Fractal
Géométrique fractale lisse: C'est une géométrie
fractale, mais avec des "cassures" à une seule échelle. Ces fractales
lisses permettent par exemple de réduire le volume d’une balle de ping-pong
sans la casser.
– histo. Imaginé en dans les années 1970 par John Nash et démontrée en 2022 par
une équipe de sept mathématiciens français (Hévéa).
En 2012, Hévéa a réussi à visualiser les
fractales lisses à courbure nulle (comme le plan). Puis en 2017, celles à
courbure négative (comme une balle). En 2022, ce sont les surfaces à courbure
positive (comme les selles à cheval).
Géométrique algorithmique: Étude des
algorithmes manipulant des objets géométriques.
– v. Polygones
isotéthiques utilisés pour modéliser les contours des objets.
– a. Computational geometry
Certaines de ces études portent sur des
problèmes purement géométriques, tandis que d'autres sont obtenues comme
corollaire de l'examen d'algorithmes géométriques de calcul. Les algorithmes de
la géométrie algorithmique sont aujourd'hui appliqués au calcul numérique, à la
modélisation géométrique, à la vision par ordinateur, à l'infographie, à la
géodésie, au calcul dynamique, à la géométrie algorithmique isothétique
et au calcul parallèle.
GF: Galois field ou corps de Galois ou corps
fini.
Giga: facteur
multiplicatif par 1 000 000 000 = 109
– ex. Un disque de 500 Go (Gigaoctets)
– v. Péfixes multiplicateurs,
milliard
Girth: en anglais courant:
synonyme de circumference.
Plutôt utilisé pour la botanique ou en anatomie (mensurations).
En géométrie dans l'espace, il signifie section de la surface projetée dans une
certaine direction.
Gisement:
angle
horizontal d'un point géographique par rapport à ma direction de progression
(vecteur vitesse).
Ou par rapport à toute autre direction qu'il faudra alors préciser.
Un gisement par rapport à la direction Nord est appelé azimut.
– v. Gisement
et cap, tangage
et roulis, gyroscope
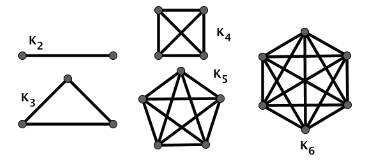
Illustration: Le navire suit
une route sans dérive. Son cap est sa direction par rapport au nord. Sur l'île,
un point de repère pour ajuster sa navigation: un amer (phare, construction,
rocher…). La direction de ce repère est son gisement.
Glèbe: terre du domaine
auquel un serf était attaché, à l’époque féodale, en sorte qu’on le vendait
avec le fonds.
Se lit 38376 sur une
calculette.
Glome**: hypersphère de dimension
quatre.
Terme plutôt anglais.
Glouton (algorithme -):
algorithme
direct ou "bestial" qui permet l'obtention du résultat sans souci de
l'optimisation des étapes pour y arriver.
– ex. L'algorithme appliqué aux
pièces en euros cherchera le jeu optimal de pièces pour atteindre une somme.
– v. Exemple pour colorier un graphe
– a. Greedy algorithm
GMP** ou GNU MP: bibliothèque logicielle de calcul multiprécision sur
des nombres entiers, rationnels et
en virgule
flottante.
Essentiellement destinée à la manipulation des très grands nombres (factorisation,
cryptographie).
Compatible Maple et Mathematica.
– v. Nombre de Fermat 12
, ECM
GMT: Greenwich Mean Time; temps moyen de
Greenwich.
Terme impropre pour temps universel coordonné (UTC).
– v. Sphère terrestre, latitude,
GPS, GMT
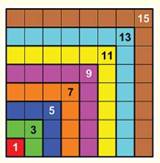Gnomon: quantité qu'il faut ajouter à une figure pour
obtenir une figure semblable.
Figure en équerre plus ou moins marquée.
– ex. pour passer du carré 2x2
au carré 3x3 il faut ajouter le gnomon 5 et pour passer au carré suivant 4x4,
il faudra ajouter 7. D'où la propriété avec les nombres
impairs: 1 + 3 + 5 + 7 + … + (2n-1) = n².
– v. Gnomon
– a. Gnomon
Gnomon: aussi un cadran qui par son
sombre, visualise le déplacement du soleil.
– a. Gnomon
Gogol: Nom du nombre valant 10100. Gogolplex = 10Gogol. Google est le moteur de
recherche.
– v. Gogle
et Gogolplex
GPS: Global Positioning System.
Système de navigation par constellation de
satellites.
Permet la localisation précise sur (et autour) de la planète (longitude,
latitude, altitude).
– note: il existe plusieurs GPS
en service dont le système européen Galileo.
Grade: il faut 400 grades
pour couvrir un cercle
(360 degrés).
100 grades pour un angle droit.
– autre nom: degré
centésimal.
– symb. gr ou gon
– v. Table
de conversion des angles
– a. Gnomon
Gradient: taux de variation
d'une grandeur au voisinage d'un point.
– ex. Gradient de température,
de potentiel …
Le gradient (pente) de la courbe vitesse-temps à un instant donné est
égal à l'accélération
instantanée.
Dans le monde des vecteurs, le
gradient est un vecteur représentant la variation d'une fonction par rapport à
la variation de ses différents paramètres.
Le gradient dans une seule direction est la dérivée simple (la pente dans le cas d'une
représentation graphique). Noté: 
.
– a. Gradient
Graduation: division régulière
d'un axe, comme sur une règle, pour repérer un point sur cet axe.
– a. Graduation (scale) /
Signifie aussi la remise de dipômes
Grandeur: dimension
en taille, longueur, largeur, hauteur.
Mais aussi valable pour toute autre quantité mesurable; terme collectif.
Propriété qui peut être mesurée ou calculée, et dont les valeurs s'expriment à
l'aide d'un nombre réel et (le plus souvnt) une unité de mesure.
– v. Grandeur, nombre,
grandeur et quantité
– a. Physical quantity: a physical
property that can be quantified by measurement.
Grandeur
produit: l'aire,
le volume sont des grandeurs produits.
Grandeur
quotient: la vitesse,
le débit sont des grandeurs quotients.
– v. Dimension, mesure, unité, amplitude
– v. Grandeur
Graphe: représentation
graphique.
L'ordre d'un graphe |V| est son nombre de sommets.
La taille d'un graphe est |E|, son nombre
d'arêtes.
Le degré ou la valence d'un sommet est le
nombre d'arêtes incidentes à ce sommet, où une boucle compte double.
– syn. Figure, diagramme.
– a. Graph, chart
Graphe d'une fonction, d'une application: courbe géométrique représentative de cette fonction, de cette application.
– v. Graphe,
couple
et graphe, vocabulaire
des structures algébriques
– a. Graph of a function
Graphe d'une relation d'un ensemble vers un autre: désigne l'ensemble
des couples formés par un élément de E et son image dans F, du fait de l'application de E dans F.
Graphe (théorie des -): étude des
propriétés de voisinage, d'interconnexion, de chemins, … entre paramètres.
Représentation sous la forme d'un réseau de courbes joignant des sommets.
– v. Graphes planaires et
autres, lexique des graphes
– a. Graph theory: A graph is made up of vertices (nodes or points) which are
connected by edges (links or lines).
Graphe en théorie des graphes, sorte de dessin fait de segments (arcs), orientés
ou non, reliés à des points dits sommets; les 
segments sont
appelés branches ou arêtes du graphe.
Un graphe est pratique pour représenter
un réseau de relations, une succession de probabilités
…
– v. Graphes – Introduction, Graphe eulérien
Graphe simple, étiqueté, complet,
planaire, connexe, graphe k-facteurs…
Illustration; exemples de graphes
complets:
– v. Vocabulaire des graphes
Graphique
(représentation graphique d'une fonction): dessin d'une courbe dans un système d'axes.
– v. Graphe, diagramme cartésien
Gravitation:
les
corps massifs s'attirent, un peu comme des aimants.
– ex. La Terre attire les
océans et provoque les marées; c'est la gravitation,
phénomène d'attraction mutuelle entre les corps matériels, dépendant de leur masse (m.m') et du
carré de leur distance (1/d²).
La gravitation ou interaction gravitationnelle est l'une des quatre forces fondamentales d'interaction
de la matière: force électromagnétique, force nucléaire forte et force
nucléaire faible.
– v. Lois de Newton, relativité générale
– a. Gravity or gravitation: all things with mass or energy are attracted
to one another.
Gravité: terme spécifique
désignant la gravitation due à la force d'interaction gravitationnelle entre la
Terre et les corps placés à proximité.
On dit aussi pesanteur ou, son effet, l'accélération de la pesanteur
ou son origine champs de pesanteur.
Le produit de la masse par l'accélération de la pesanteur (g = 9,81 m.s-2)
donne le poids d'un objet sur la Terre (ou
autres astres, comme la Lune).
– v. Pesanteur, poids et altitude,
accélération
– a. Gravitational acceleration
Gravité (centre de -): point sur lequel un
objet tient en équilibre.
Les médianes
d'un triangle
se coupent au centre de gravité du triangle.
– ex. Un triangle en carton tient en équilibre
si on pose le centre de gravité sur la pointe d'un crayon.
Centre de gravité ou centre de masse ou centre d'inertie:
point d’application de la résultante des forces gravitationnelles pour un corps
matériel, quelle que soit la position de ce corps.
– v. Centre de gravité, calcul
du centre de gravité, barycentre,
centre d'inertie
– a. Gravity center, center of mass, centroïd
Grec (lettres -): les 24 lettres de
l'alphabet grec dont certaine sont tès utilisées en maths et en physique.
– ex. 
– note: La première
est alpha et la deuxième est bêta, origine du mot alphabet.
La première est alpha et la
dernière est oméga, origine de l'expression de l'alpha à l'oméga
– v. Alphabet grec, Alphabet en maths, sciences et langue
– a. Greek alphabet
Gréco-latin (carré -): grilles carrées
remplies de deux nombres (ou objets), un
objet unique sur chaque ligne et sur chaque colonne, et un seul couple par
ligne et par colonne.
Il est formé par la superposition de deux carrés latins orthogonaux.
– v. Carré gréco-latin, carré latin,
mathématique
des carrés gréco-latins, carré
magique, sudoku
– a. Graeco-latin square, mutually orthogonal Latin
squares
Grille: quadrillage
régulier.
– Syn. Réseau, quadrillage
– Ex. Grille 4 ×
4 sur laquelle on compte les chemins pour aller du bas gauche au haut droit en
montant, en allant à droite ou en montant en
diagonale. 39 chemins possibles.
– v. Nombres
de Delannoy, Taxi
dans Manhattan
– a. Grid
Grillion: mot générique qui,
dans le langage courant, désigne une grande quantité, comme de mot zillion.
– v. Noms
des petits et grands nombres
Groupe*
ensemble
avec (muni d') une loi
de composition interne, associative, possédant un élément neutre et telle
que tout élément admette un symétrique pour cette loi.
C'est cas de l'ensemble des nombres entiers avec l'addition.
– v. Groupe, anneau, corps,
structure
algébrique, espace
vectoriel, vocabulaire
des structures algébriques
Groupe cyclique: qui possède un élément générateur et ses multiples. Il
est monogène.
Il existe un élément a, le générateur du groupe, tel que tout élément du
groupe puisse s'exprimer sous forme d'un multiple de a.
– v. Groupe cyclique, vocabulaire
des structures algébriques
– a.
Cyclic group or monogenous group: that is generated by a single element.
Groupes simples finis: qui possède une quantité finie d'éléments et qui
ne possède pas de sous-groupe particulier.
Leur classification fut terminée en 1983 et elle compte cinq catégories dont
les groupes sporadiques et parmi eux le groupe monstre.
– a. Finite simple group
Groupes de permutations, groupes isomorphes: Voir vocabulaire
des structures algébriques
Un groupe de permutations G est un groupe fini dont les éléments sont les
permutations d'un ensemble donné et dont les opérations sur le groupe est la
composition des permutations dans G.
– ex. Le groupe des
symétries Sn est un groupe de permutations d'ordre n!
– v. Groupes
de permutations
– a. Permutation group
Groupe de Galois: groupe impliqué dans la caractérisation des symétries
des racines de polynômes.
En 1832, Évariste Galois
montre qu'il est impossible de résoudre des équations
supérieures au quatrième degré. En revanche, il est possible de caractériser
les relations entres les racines et de mettre en évidence leurs symétries. Par
exemple x² – 2 = 0 a deux racines symétriques: 
.
–
v. Langlands Program,
nombres p-adiques
Gyroscope:
c'est
une toupie professionnelle.
Propriété majeure: l'axe de
rotation tend à conserver sa direction initiale quels que soient les mouvements
environnants;
– ex. Les roues d'un
vélo ont un effet gyroscopique qui participe au maintien de votre équilibre sur
le vélo en mouvement.
Le gyromètre mesure la vitesse
angulaire.
– ex. les gyromètres
sont utilisés dans les sous-marins
comme élément de référence pour déterminer la longitude; l'instrument complet
comportant trois gyroscopes s'appelle la centrale à inertie (on centrale
inertielle).
– v. Gisement, azimut,
rotation, précession, nutation.
– v. Gisement
et cap, tangage
et roulis, emploi du GPS
– a.
Gyroscope
|
Voir |
|
|
Aussi |
|
|
Autres |
|
|
Cette page |
