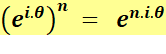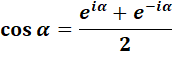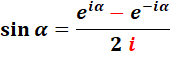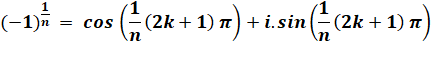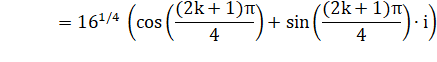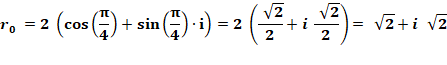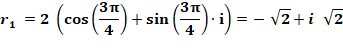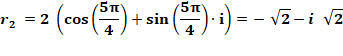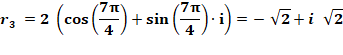|
||||||||||||||||||||||||||
![]()
|
Nombres complexes RACINES La forme polaire se prête aisément au calcul de
la racine nième d'un nombre complexe. |
|
Abraham de Moivre (1667
– 1754 / 87 ans) Mathématicien français. Pour des raisons religieuses, il est
emprisonné (1685 à 1688), puis s'exile en Angleterre. Rappel: 1685 –
révocation de l'édit de Nantes par Louis XIV. À Londres, il rencontre Halley
et Newton, puis Leibniz. Étant âgé, il déclare qu’il lui est
nécessaire de dormir chaque nuit ¼ heure de plus que la nuit précédente. En
calculant cette progression arithmétique, il en déduisit le jour de sa mort.
Et, effectivement, la nuit dépassant les 24 heures, il est mort durant son
sommeil ! Rapporté par David
Wells. La formule de Stirling pour calculer les
grandes factorielles doit beaucoup à la formule initiale de De Moivre. |
|
|
|
|
Formule
de Moivre (vers
1730)
n étant un nombre
entier Note: parfois cos Écriture avec parenthèses, si confusion possible
Écriture
exponentielle
Formules
d'Euler
(Rappel)
La formule de De Moivre serait plutôt due à Euler (1748)
qui l'a énoncée sans vraiment la démontrer. |
|
Voir Euler / Formule
et identité d'Euler / Les quatre
constantes / Trigonométrie / Exponentielle
Application a la linéarisation
des fonctions trigonométriques
|
|
|||
|
z |
= |
r (cos |
|
|
z n |
= |
r n ( cos n |
|
|
(cos |
= |
cos (n |
|
|
ln z |
= |
ln r + i |
|
|
|
= |
|
|
|
(cos La formule se démontre par récurrence en utilisant cette
identité. |
|||
|
|
|
|
|
|
|
|
|
|
Principe Le calcul passe par la connaissance de la racine énième
de (-1):
Avec théta = (2k + 1) Pi:
Exemple avec racine quatrième de -16
Avec k = 0, 1, 2, 3, on trouve:
|
|
Voir Racines quatrièmes
|
|
||
|
|
|
|
|
|
|
|
|
|
a = r (cos b = r (cos |
|
|
|
|
|
|
Les
racines (comme les puissances) de
nombres conjugués restent conjuguées. Leur somme est un nombre réel. |
||
|
Pour information
|
= 1 + 1, 732… i
|
|
|
|
= 1,259921050…
(0,9396926208…
+ 0,3420201433… i) = 1,183938513… + 0,4309183781… i |
|
Bilan
|
La
formule de Moivre permet de calculer les valeurs des sinus et cosinus des multiples et fractions des angles. |
Voir Formulaire de
trigonométrie
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/Moivre.htm |
![]()