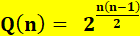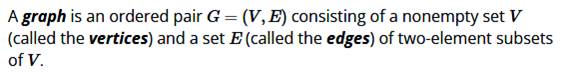Graphes, introduction et types

Édition du: 22/05/2023

M'écrire

Brèves de Maths

INDEX

Graphe

Topologie

Dénombrement

GRAPHES

Graphes – Introduction

Arbres – Introduction

Graphes – Vocabulaire

Nœuds

Croisements

Nombres de Ramsey

Faites un double-clic pour un retour en haut de page

GRAPHES

Introduction et types de Graphes

Un réseau routier est un graphe. Un arbre généalogique est un graphe. Un algorithme est un graphe. La planification repose sur des graphes. La régulation des flux d'avions passe par les graphes. Etc.

Le problème des ponts de Königsberg est un exemple d'application des graphes. Euler en donna la solution et il est devenu le précurseur de la théorie des graphes.

La théorie de résolution du Sudoku comme celle du Rubik's cube profitent de la théorie des graphes.

Les moteurs de recherche ne pourraient pas être étudiés sans les graphes. Le mot anglais WEB ne signifie-t-il pas toile d'araignée !

Sommaire de cette page

>>> Graphes

>>> Caractérisation des graphes

>>> Graphes finis

>>> Graphes simples

>>> Graphes multiples

>>> Graphes complets

>>> Graphes bipartis

>>> Graphes étiquetés

>>> Graphes colorés

>>> Graphe coloré du Sudoku

>>> Quantité de graphes

>>> English corner

Débutants

Dénombrement

Glossaire

Combinatoire

Français: Graphe – divers sens / Anglais : Graph

Graphe - Graph			haut
Définition Un graphe est une structure de données non linéaire constituée de nœuds et d'arêtes. Les nœuds sont parfois également appelés sommets et les arêtes sont des lignes ou des arcs qui relient deux nœuds quelconques du graphe. Plus formellement, un graphe peut être défini comme un graphe composé d'un ensemble fini de sommets (ou de nœuds) et d'un ensemble d'arêtes qui relient une paire de nœuds. 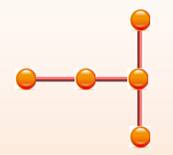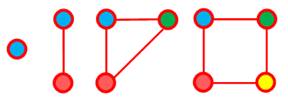Désignation G pour graphe, S pour sommet et A pour arêtes: G(S, A)		Exemples de graphes
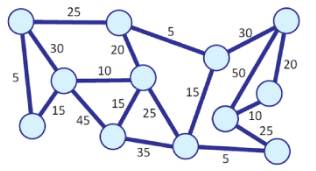
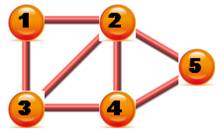
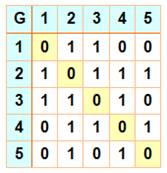
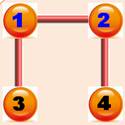
Représentation par une matrice Sur la ligne 1 de la matrice qui représente le nœud 1 du graphe, on trouve à "1" ses connexions avec les autres nœuds en 2 et 3. La diagonale descendante est à 0; pas de boucle sur les sommets.
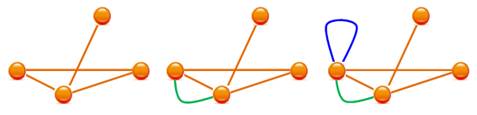
Degré des sommets C'est la quantité d'arêtes aboutissant à ce sommet. Règle des sommets-arêtes La quantité d'arêtes est égale à la moitié de la somme des degrés.	Suite des degrés des sommets du graphe ci-dessus S = (2, 4, 3, 3, 2) Somme: 14 Le graphe compte: 14 / 2 = 7 arêtes

Devinette: application de la règle des sommets-arêtes

Une assemblée de neuf personnes. On se sert la main en signe de bienvenue. Est-il possible que chaque personne salue sept personnes exactement ?

Ce problème revient à considérer un graphe à neuf sommets dont chacun aurait un degré égal à 7.

Le somme des degrés serait 9 × 7 = 63, un nombre impair, donc non divisible par 2. Ce cas est impossible selon la règle des sommets-arêtes.

Réalisable si au moins un (en fait un nombre impair) de personnes avait serré la main d'un nombre pair de personnes dans l'assemblée.

Cette fois, ils sont dix. Ils se saluent tous. Combien de poignées de mains ?

Ce problème revient à considérer un graphe à dix sommets dont chacun relie les neuf autres.

La somme des degrés vaut: 10 × 9 = 90. Le graphe possède 45 arêtes.

Il y a eu 45 poignées de mains.

Un groupe de cinq personnes. Il est possible pour chacun d'être ami avec deux autres. Mis en cercle, chacun peut être ami avec ses deux voisins.

Mais avec trois personnes c'est impossible. La somme des degré serait 5 ×3 = 15, un nombre impair. Impossible.

Voir Brève 49-977

Caractérisation des graphes

haut

Graphes non orientés (undirected graph) : un graphe dans lequel les arêtes n'ont pas de direction, c'est-à-dire que les arêtes n'ont pas de flèches indiquant la direction de parcours.
Exemple : Un graphique de réseau social où les amitiés ne sont pas directionnelles.

Graphes orientés (directed graph) : un graphe dans lequel les arêtes ont une direction, c'est-à-dire que les arêtes ont des flèches indiquant la direction de la traversée.
Exemple : Un graphique de page Web où les liens entre les pages sont directionnels.

Graphiques pondérés (weighted graph) : un graphique dans lequel les arêtes ont des poids ou des coûts qui leur sont associés.
Exemple : Un graphique de réseau routier où les poids peuvent représenter la distance entre deux villes.

Graphiques non pondérés (unweighted graph) : un graphique dans lequel les arêtes n'ont pas de poids ou de coûts associés.
Exemple : Un graphique de réseau social où les arêtes représentent des amitiés.

Graphes complets (complete graph) : un graphe dans lequel chaque sommet est connecté à tous les autres sommets.
Exemple : Un graphique de tournoi où chaque joueur joue contre tous les autres joueurs.

Graphes bipartis (bipartite graph) : un graphe dans lequel les sommets peuvent être divisés en deux ensembles disjoints de sorte que chaque arête relie un sommet d'un ensemble à un sommet de l'autre ensemble.
Exemple : Un graphique de demandeur d'emploi où les sommets peuvent être divisés en demandeurs d'emploi et en offres d'emploi.

Arbres (tree) : un graphe connexe (ou en un seul morceau) sans cycles (ou sans boucle).
Exemple : Un arbre généalogique où chaque personne est liée à ses parents.

Graphe avec cycles (cycle) : un graphique avec au moins un cycle (une boucle).
Exemple : Un graphique de vélos en libre-service où les vélos représentent les itinéraires empruntés par les vélos. La boucle est le retour au point de stationnement initial.

Graphes creux (sparse graph) : un graphe avec relativement peu d'arêtes par rapport au nombre de sommets.
Exemple : Un graphique de réaction chimique où chaque sommet représente un composé chimique et chaque arête représente une réaction entre deux composés.

Graphes denses (dense graph) : un graphe avec de nombreuses arêtes par rapport au nombre de sommets.
Exemple : Un graphe de réseau social où chaque sommet représente une personne et chaque arête représente une amitié.

Graphes coloré (coloured graph) : un graphe dont les sommets sont colorés sans que les sommets adjacents soient de la même couleur. Deux sommets sont adjacents s'ils sont reliés par une arête.

Chemin d'Euler (Euler path) : un chemin qui passe par toutes les arêtes une seule fois.

Circuit d'Euler (Euler circuit) : un chemin d'Euler qui commence et finit au même sommet.

Clique (clique) : un sous-graphe complet d'un graphe: deux sommets quelconques de la clique sont toujours adjacents. Le nombre chromatique d'un graphe est supérieur ou égal au nombre de sommets dans sa plus grande clique.

D'après Types of Graphs with Examples – Geeksforgeeks

Voir Vocabulaire des graphes

Graphe fini – Finite graph

haut

Graphe dont la quantité de sommets et la quantité d'arêtes sont caractérisés par des nombres entiers non infinis.

Exemples de graphes fini et infini

Graphe simple – Simple graph or strict graph

haut

Graphe avec seulement une arête entre chaque pair de sommets.

Pas de boucles et pas d'arêtes multiples: cas de deux arêtes ou plus connectant deux sommets.

Exemple de graphe simple

& contre-exemples sans boucle et avec boucle

Voir Graphes simples – Développements

Graphe multiple – Multi graph

haut

Graphe avec un nombre quelconque d'arêtes par sommet et qui peut contenir des boucles mais jamais de boucle sur un sommet.

Exemple de graphe multiple

Graphe planaire – Planar graph

haut

Graphe tel qu'il est possible de le construire sans croisement des arêtes.

Ces trois graphes sont semblables (isomorphiques). Ils se déduisent les uns des autres par déplacement des sommets.

Ils sont tous les trois planaires.

Exemples de graphes planaires

Graphe complet – Complete graph

haut

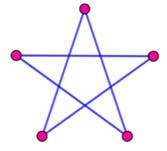
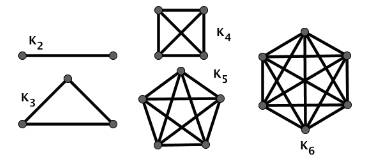
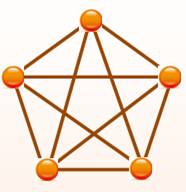
Graphe dont chaque sommet est relié à tous les autres.

Si le graphe compte n nœuds, chaque nœud recevra n – 1 arêtes.

Les premiers types de graphes complets

Exemple de graphe complet (K₅)

Un graphe complet de n sommets compte n (n – 1) / 2 arêtes.

Graphe biparti – Bipartite graph

haut

Graphe comportant deux ensembles de sommets.

Chaque sommet de l'un est relié à un sommet de l'autre

Exemple de graphe biparti

Graphe étiqueté – Labeled graph		haut
Graphe dont les sommets ou les arêtes sont numérotés. Intérêt en informatique: algorithme et programmation. Voir Arbres étiquetés	Exemple de graphe étiqueté (sommet)
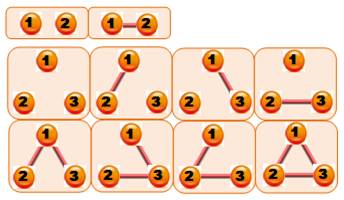
Quantité de graphes étiquetés On dénombre deux graphes pour deux sommets et huit pour trois sommets. La quantité de tous les graphes étiquetés pour n sommets est: Soit la suite: 1, 2, 8, 64, 1024, 32768, 2097152, 268435456, 68719476736, 35184372088832, … Quantité de graphes étiquetés complets Tous les sommets sont reliés 1, 1, 4, 38, 728, 26704, 1866256, 251548592, 66296291072, …	Graphes étiquetés pour n = 2 et n = 3

Graphe coloré – Colored graph

haut

Graphe coloré

Graphe dont les sommets sont repérés par une couleur.

Le minimum de couleurs nécessaires pour colorier un graphe sans la même couleur sur deux sommets adjacents est le nombre chromatique du graphe.

Problème des quatre couleurs

Le problème des quatre couleurs est pose dès 1852 jusqu'à ce qu'en 1879 l'avocat Alfred Kempe propose une preuve. Elle s'est révélée fausse, mais son principe était original: utilisation d'un graphe.

L'idée consiste à remplacer les pays par les sommets d'un graphe et les frontières communes sont matérialisées par un trait (une arête).

Le problème de coloration de la carte devient u problème de coloration du graphe.

Le problème devient: prouver que le nombre chromatique d'un graphe de carte est quatre.

Ce graphe de "carte" est particulier. Il est:

planaire: pas de croisements entre arêtes;

simple: une seule arête entre deux sommets, et pas de boucle sur un sommet.

Finalement, le problème des quatre couleurs devient:

Prouver que le nombre chromatique de tout graphe simple et planaire est au plus égal à quatre.

Prove that the chromatic number of every simple planar graph is at most four.

Nombre chromatique

Quatre couleurs au plus suffisent pour jusqu'à quatre sommets.

Exemple de graphe coloré représentant une carte géographique

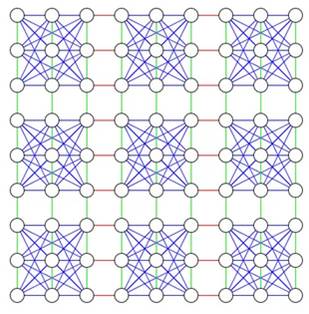
Graphe coloré du Sudoku – Sudoku graph			haut
Graphe coloré du Sudoku La grille du Sudoku comporte 9 × 9 = 81 cases. Chaque cellule contient un chiffre qui n'est pas l'un des 20 cellules en ligne, colonne et région (8 + 8 + 4). Le graphe est un graphe à 81 sommets, chacun de degré 20 et qui donc a 810 arêtes. Il s'agit de colorier la cellule rouge avec une couleur différente des vingt autres. Une version isomorphe du graphe complet du Sudoku		Relation Sudoku Graphe simplifié du Sudoku
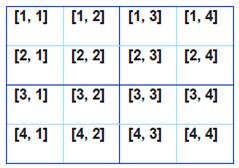
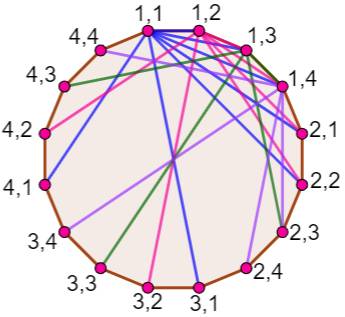
Sudoku 4 × 4 – Codage des cellules Chaque cellule est codée par une paire de nombres.	Graphe du Sudoku 4 × 4 – une seule région représentée

Un échantillon des types de graphes et de leur dénombrement

Types	(S, A)	OEIS	Quantité de motifs
Graphes simples	*Sommets*	A000048	1, 2, 4, 11, 34, 156, 1044, 12346, 274668, 12005168, 1018997864, 165091172592, …
Graphes simples	*Arêtes*	A086314	0, 1, 6, 33, 170, 1170, 10962, 172844, 4944024, 270116280, 28022441260, ...
Graphes étiquetés	*Sommets*	A095340	1, 4, 24, 256, 5120, 196608, 14680064, 2147483648, 618475290624, ...
Graphes étiquetés	*Arêtes*	A095351	0, 1, 12, 192, 5120, 245760, 22020096, 3758096384, 1236950581248, ...
Arbres étiquetés	*Sommets*	A000169	1, 2, 9, 64, 625, 7776, 117649, 2097152, 43046721, 1000000000, 25937424601, ...
Arbres étiquetés	*Arêtes*	A053506	0, 1, 6, 48, 500, 6480, 100842, 1835008, 38263752, 900000000,...
Arbre plantés	*Sommets*	A095341	0, 2, 3, 8, 20, 54, 140, 384, 1035, 2860, 7909, 22104, 61958, 174804, ...
Arbre plantés	*Arêtes*	A055544	0, 1, 2, 6, 16, 45, 120, 336, 920, 2574, 7190, 20262, 57192, 162318, 461622, ...
Arbres enracinés	*Sommets*	A055545	1, 2, 6, 16, 45, 120, 336, 920, 2574, 7190, 20262, 57192, 162318, 461622, ...
Arbres enracinés	*Arêtes*	A095350	0, 1, 4, 12, 36, 100, 288, 805, 2288, 6471, 18420, 52426, ...
Arbres	*Sommets*	A055543	1, 2, 3, 8, 15, 36, 77, 184, 423, 1060, 2585, 6612, 16913, 44226, ...
Arbres	*Arêtes*	A095349	0, 1, 2, 6, 12, 30, 66, 161, 376, 954, 2350, 6061, 15612, 41067, ...

Se reporter aux liens pour des informations plus précises

English corner

Definition

Isomorphism

An isomorphism is simply a function which renames the vertices. It must be a bijection so every vertex gets a new name. These newly named vertices must be connected by edges precisely when they were connected by edges with their old names.

Handshake Lemma: In any graph, the sum of the degrees of vertices in the graph is always twice the number of edges.
Ex: vertice degree sequence: (4, 4, 3, 3, 3, 2, 1). Sum = 20. The number of edges is half this: 10.

Voir Anglais pour le bac et pour les affaires

Haut de page

Retour	Graphe planaire Graphes – Index
Suite	Arbres à dénombrement avec nombres de Catalan Arbres de distribution Chemin le plus court Vocabulaire des graphes	Coloration des graphes (nombre chromatique) Graphes et problèmes NP Petit monde Sept amis autour d'une table
Voir	Code Gray Croissance logistique Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index	Logique formelle Percolation Relier les points d'un seul coup de crayon Topologie – Glossaire Tour de Brahmâ Trois maisons (énigme des -)
Sites	Types of Graphs with Examples – Geeksforgeeks Discrete Mathematics: An Open Introduction, 3rd edition – Oscar Levin – Cours complet avec exercices corrigés *OEIS A006125 – a(n) = 2^(n(n-1)/2) OEIS A001187 – Number of connected labeled graphs with n nodes Graph Classes – ISGCI –** Sorte d'encyclopédie des graphes Sudoku graph – Wikipedia Visualizing the Sudoku Connectivity Graph – reddit – Graphes animé du Sudoku 9x9
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/Graphe.htm