Dictionnaire de base du vocabulaire des mathématiques F

Face: chacune des surfaces (du type polygone) délimitant un polyèdre.
– ex. Le cube est un polyèdre à six faces carrées.
– étym. Du grec hedra, face
– v. Arête, sommet, théorème de Descartes-Euler (S+ F = A+ 2).
– a. Face: a three-dimensional solid bounded exclusively by faces is a polyhedron.

Face d'un solide: surface plane ou courbe délimitée par des arêtes.
– a. Face of a solid

Face latérale (ou surface latérale): par opposition à la base dans une pyramide ou un prisme.
– ex. La surface latérale d'un cône
– a. Lateral face, lateral area

Facteur: chacun des nombres d'un produit (arithmétique) ou autre élément constitutif d'un produit (algèbre)
– étym. Du latin factor, celui qui fait
– v. Multiplication, terme,
– a. Factor

Un facteur est un des termes d’un produit.

Par exemple, 2 x 3 comporte deux facteurs : 2 et 3.

Mettre un terme en facteur dans une expression algébrique, c’est utiliser la distributivité de la multiplication par rapport à l’addition, pour écrire l’expression sous la forme d’un produit.

Par exemple, dans l’expression : (x – 2)(2x + 3) – (x – 2)(x + I), on peut mettre (x – 2) en facteur : (x – 2) [(2x + 3) – (x + I)] = (x – 2) (x + 2).

Facteur premier: nombre premier qui divise un nombre.
– ex. Dans 12 = 2 x 2 x 3, les nombres 2 et 3 sont des facteurs premiers ou diviseurs premiers
– v. Facteurs
– a. Prime factor

Facteur: mettre en facteur commun: simplification telle que ab + ac = a (b + c), qui se lit a facteur de b plus c. On peut dire plus simplement: factoriser le polynôme.
– v. Factorisation, décomposition
– v. Développer, jargon , expressions algébriques, identités remarquables
– a. Factorize

Factorielle: produit des nombres successifs.
– notation: n!
– ex. 6! = 1 x 2 x 3 x 4 x 5 x 6 = 720).
– ortho. Une factorielle, nom qui s'écrit avec "lle".
– v. Factorielles, combinaisons, formule de Stirling
– a. The factorial of a non-negative integer, denoted by n!, is the product of all positive integers less than or equal to n.

Si n est un nombre entier naturel (positif), on appelle factorielle n, et on note n ! (lire : factorielle n), le produit de tous les entiers consécutifs depuis 1 jusqu’à n. Par exemple : 3! = 1 x 2 x 3 ; 5 ! = l x 2 x 3 x 4 x 5.

Le cas de 0! n’a pas d’existence selon la définition ci-dessus. Par convention, on pose: 0! = 1 pour que la formule suivante soit vraie si n = p:

Factorielle (analyse -)*: méthode statistique ayant pour but de chercher les facteurs communs à un ensemble de variables qui ont entre elles de fortes corrélations.
– a. Factor analysis

Factorisation d'un nombre, factorisation primaire: trouver tous les facteurs d'un nombre (facteur = diviseur premier).
Théorème fondamental de l'arithmétique: ce produit est unique, à l'ordre des facteurs près
– ex. 504 = 7 x 8 x 9.
– note: 504 = 1 x 7 x 8 x 9 = 1 x 1 x 7 x 8 x 9 … Cette multiplicité expliqua pourquoi le nombre 1 n'est pas considéré comme un nombre premier
– v. Développement, distributivité
– a. Factoring (US), factorising (UK), finding the factors, fundamental theorem of arithmetic or unique factorization theorem

Factorisation des grands nombres*: la cryptographie utilise des nombres composés dont les facteurs premiers sont de très grands nombres.
Décoder un message crypté nécessiterait de retrouver ces facteurs, ce qui est très difficile.
Les mathématiciens recherchent des algorithmes, d'une part, pour déjouer le décryptage, et d'autre part, pour tester la difficulté de retrouver les facteurs et, au total, assurer une sécurité de transmission.
– v. Cryptologie, RSA
– a. Factorization of large numbers

Factorisation d'une expression: synonyme de factoriser un polynôme >>>

Factorisation d'un polynôme: transformation d'une somme algébrique en un produit; trouver les facteurs communs; ex: ab + ac = a(b+c); ou moins évident a priori: a² - b² = (a - b) (a + b); etc. Contraire: développer
– v. Théorème de factorisation, développer et factoriser, mots usuels du calcul, techniques de base de l'algèbre, Identités remarquables
– a. Factorization of polynomials

Forme factorisée du trinôme: f(x) = (x – R₁)(x – R₂)
– v. Forme polynomiale du second degré: développée, factorisée ou canonique
– a. Factorized polynomial

Faisceau: famille d'objets géométriques partageant une propriété commune, par exemple l'ensemble de droites passant par un même point dans le plan, ou l'ensemble de cercles passant par deux points dans le plan.

Faisceau de droites: l'ensemble des droites passant par un point de l'espace 3D est un fibré de droites, deux d'entre elles caractérisant un faisceau de droites.
– a. Pencil: family of geometric objects with a common property.

Un faisceau de droites est constitué:

soit par des droites toutes parallèles entre elles si (C) et (C’) sont deux droites parallèles;

soit par des droites passant toutes par le même point (si (C) et (C’) sont deux droites concourantes).

Faisceau de courbes: si (C) et (C’) sont deux courbes planes d’équations respectives f(x, y) = 0 et g(x, y) = 0, on appelle faisceau linéaire engendré par (C) et (C’) l’ensemble de toutes les courbes du plan dont l’équation est de la forme : f(x, y) + λg(x, y) = 0, où λ est un nombre réel quelconque.
Si les deux courbes (C) et (CI’) se coupent en un certain nombre de points, toutes les courbes du faisceau passent par ces points.
– a. Pencil of curves

Faisceau de cercles: dans un plan, cercles passant par deux points donnés.
– a. Pencil of circles or coaxial system: set of all circles in the plane with the same radical axis.

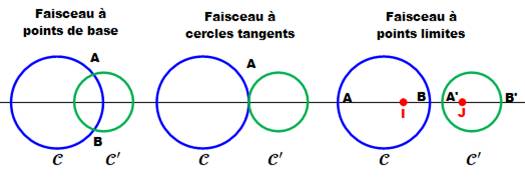
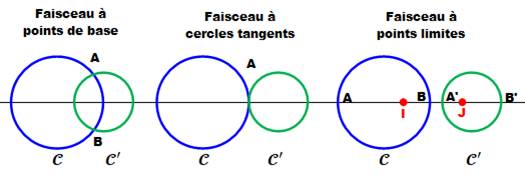
Il y a trois types de faisceau de cercles :

Si les deux cercles (C) et (C’) se coupent en A et B, tous les cercles du faisceau passent par A et B ; A et B sont appelés points de base du faisceau. La droite AB est l'axe radical et la droite des centres est la médiatrice du segment AB.

Si (C) et (C’) sont tangents en A, tous les cercles du faisceau passent par A et sont tangents en A. La droite de tangente est l'axe radical

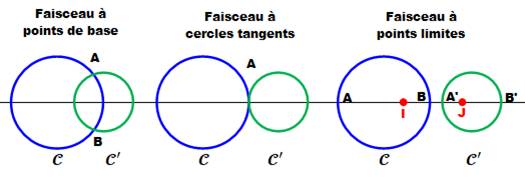
Si (C) et (C’) ne se coupent pas, sur la droite (D) joignant les centres des deux cercles il existe deux points I et J tels que les divisions A, B, I, J et A’, B’, I, J sont harmoniques. Les points et I et J sont appelés points limites du faisceau ou points de Poncelet.

Plus précisément: étant donné une droite (d) et un cercle (C) n'ayant pas de point commun, K est la projection du centre O sur (d) et M un des points de contact d'une tangente issue de K.

L'ensemble des cercles admettant (d) comme axe radical est l'ensemble des cercles dont les extrémités d'un diamètre divisent harmoniquement le segment [IJ], les points I et J étant tels que : KI² = KJ² = KT², puissance du point K par rapport au cercle (C).

I et J sont les intersections du cercle de centre K passant par M avec la ligne des centres (OK). On dit que ces cercles forment un faisceau déterminé par (C) et (d).

Faisceau de cercles orthogonaux: collection de cercles orthogonaux à la fois à deux cercles distincts (non concentriques).

Fausse (proposition -): affirmation réputée non-conforme à la réalité.
– ex. L'araignée est un insecte est une affirmation fausse.
– v. Vraie, improbable
– a. False

Méthode de la fausse position: la méthode de la fausse position consiste à deviner la réponse, même si elle est fausse. Le raisonnement permettra de corriger.
– v. Méthode de la fausse position
– a. Factorized

Fermat (nombre de -)*: nombre de la forme F_n = 2^d + 1 avec d = 2ⁿ, une puissance de 2.
Un nombre de Fermat n'est pas nécessairement un nombre premier.
Un nombre premier de la forme 2^k + 1 est un nombre de Fermat et k = 2ⁿ.
– v. Nombre de Fermat
– a. Fermat numbers: named after Pierre de Fermat, who first studied them

Fermat (petit théorème -)*: ce théorème énonce une propriété d'un nombre (a) face à un nombre premier (p).
Le nombre et sa puissance p donne le même reste lorsqu'ils sont divisés par p.
– formulation avec les congruences:

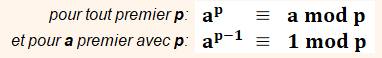
– ex: 3^5-1 = 81 et 81 = 16 x 5 + 1

Fermat (théorème de Fermat- Wiles)** aucun nombres ne peuvent satisfaire l'identité suivante: xⁿ + yⁿ = zⁿ pour n > 2
– v. Théorème de Fermat-Wiles
– a. Fermat's Last Theorem (FLT)

Fermat (point de -)* dans un triangle, c'est le point tel que les droites rejoignant les sommets fassent entre-elles un angle de 120°.
Dans ce cas, la somme des distances de ce point aux sommets est minimale.
Si les angles du triangle sont supérieurs à 120°, le point de Fermat est l'un des sommets.
– v. Point de Fermat
– a. Fermat point of a triangle, Torricelli point or Fermat–Torricelli point.

Fermé (ensemble -)* ensemble tel qu'une opération qui lui est appliquée donne un résultat qui reste dans l'ensemble lui-même.
– ex: l'addition sur les nombres positifs, ou les symétries du carré.
La division sur les nombres entiers n'est pas fermée, il faut faire appel aux nombres réels pour cela.
– v. Stable et Clos, ensemble clos et ensemble ouvert
– a. Closed set and open set

Si E est un espace topologique, on appelle partie fermée de E, ou, plus simplement fermé de E, tout sous-ensemble de E dont le complémentaire dans E est un ouvert de E.
Les propriétés des fermés se déduisent immédiatement de celles des ouverts :

a) toute intersection de fermés est un fermé ;

b) toute réunion finie de fermés est un fermé ;

c) E et 0 sont des fermés.

Comme il est équivalent de se donner le système d’ouverts de E ou le système de fermés, on pourrait définir une topologie sur un ensemble E à partir d’une famille F de fermés.

FFT (Fast Fourier Transform)**: transformée de Fourier rapide.
– v. Multiplication rapide

Transformée de Fourier: sorte d'analyse spectrale d'un signal.
– v. Transformée et série de Fourier
– a. Fourier transform

Fibonacci (suite de -): nombre de la suite 1, 1, 2, 3, 5, 8 … dans laquelle chaque nombre est la somme de ses deux prédécesseurs.
– v. Suite de Fibonacci
– a. Fibonacci numbers

Fidélité: en métrologie, aptitude à donner des mesures proches lors de mesures répétées.
Exempt d'erreurs accidentelles.
Caractérisée par la dispersion des résultats.
– v. Incertitude et précision, résolution, sensibilité, exactitude

Figure: synonyme de dessin.
Illustration qui aide à poser un énoncé ou à suivre un raisonnement, une démonstration.

Figure géométrique (figure): une figure est un ensemble de points.
Une figure est une entité mathématique comprenant points, lignes, surfaces et volumes.
– v. Figure, graphe, diagramme, transformations
– a. Geometric figure or geometric shape

Figure plane: figure totalement contenue dans un plan.
– ex: rectangle, carré, cercle …
– a. Plane figure

Figure gauche: figure qui n'est pas plane; figure ou courbe dessinées sur un plan courbé.

Figure dans l'espace: figure en trois dimensions.
– ex: Sphère, cône, parallélépipède …, Stéréométrie
– a. Space shape, 3D shape, solid geometry

Figure rectiligne: figure limitée par les lignes droites.
– a. Straight line figures, straight figures

Figure curviligne: figure non rectiligne; limitée par les lignes courbes.
Curvilinear shapes or patterns

Figure invariante: la figure coïncide avec sa transformée; T(F) = F.
– a. Invariant figure, invariant shape

Figure symétrique: figure qui présente un axe de symétrie ou un centre de symétrie.
– v. Semblable, homothétique
– a. Symmetrical shapes; these geometrical figures are symmetrical; this geometric shape has 3-fold rotatio;al symmetry.

Filtre: dispositif destiné à séparer des éléments.
– a. filter, screen

Filtre (électronique): dispositif destiné à ne laisser passer qu'une partie des fréquences qu'il reçoit.
Parmi eux, les filtres passe-bas, passe-haut et passe-bande.
Leur étude fait appel aux principes du traitement du signal.
– a. Electronic filter

Filtrage spatial: dispositif destiné à ne laisser recueillir un signal dans une direction donnée.
Cette opération procède par formation de voies spatiales chacune traitée indépendamment.
– a. Beamforming

Exemple du filtrage spatial des sonars: le signal de chaque voie est décalé dans le temps pour tenir compte de la courbure des antennes et, surtout, de la courbure (sphérique) du signal d'arrivée.
Exemple du filtrage spatial adaptatif des télescopes: les fluctuations du signal dues à la traversée de l'atmosphère sont évaluées dans un secteur plus large que la voie visée, et le signal dans cette voie est traité pour minimiser l'influence de cette perturbation

Filtrage (topologie): structure définie sur un ensemble, permettant d’étendre la notion de limite.

Soient E un ensemble et A une partie non vide de cet ensemble. Appelons F la famille de toutes les parties de E qui contiennent A.
Cette famille F n’est pas vide (il y a au moins E qui en fait partie) ; l’ensemble vide 0 n’appartient pas à cette famille (l’ensemble vide ne peut contenir un ensemble non vide) ; si B est un élément de cette famille et si C est une partie de E qui contient B, alors C appartient à la famille F (puisque C contient B qui contient A, C contient donc A).
Si B et C sont deux éléments de la famille F, tous deux contiennent A ; leur intersection contient donc aussi A; elle appartient à la famille F.
On dit que cette famille F est un filtre sur l’ensemble E.
En fait, un filtre F sur un ensemble E est un ensemble de parties de E qui satisfait à certains conditions précises (par exemple: F n'est pas vide et l'ensemble vide n'appartient pas à F).

Fini (ensemble -): dont on peut compter la quantité d'éléments.
Cette quantité est appelé le cardinal de l'ensemble.
– ex: L'ensemble des restes de la division par 3 est fini; ses éléments sont {0, 1, 2}.
– v. Théorie des ensembles
– a. Finite set; {1, 3, 5, 7, 10} is a finite set of five elements.

Flèche: hauteur de la surface formée par un arc de cercle et sa corde;
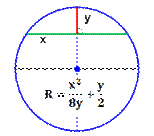Ce segment est situé sur le diamètre perpendiculaire à la corde, qui est axe de symétrie de la figure.
Segment reliant les milieux d'un arc et d'une corde définis par deux mêmes points.
Si est l'angle interceptant l'arc de cercle, la flèche mesure:

– v. Arcs, cordes et sagittas, corde, sagitta, versin
– a. Sagitta, versine

Flocon de neige: fractale formée par trois lignes de Koch appliquée à chacun des côtés d'un triangle équilatéral.
– v. Courbe de Koch dite flocon de neige.
– a. Koch Snowflake.

Flottant (virgule -)*: mode de représentation des nombres avec une résolution adaptée à la capacité de sa représentation en mémoire d'ordinateur.
– v. Virgule flottante
– proche: Notation scientifique
– a. Floating point (FP)

FLOU (Mathématique du -): la logique qui sous-tend toute l’architecture mathématique traditionnelle est une logique binaire ; on dit qu’elle est bivalente ou qu’elle a deux valeurs de vérité, et deux seulement. Cela signifie simplement qu’une proposition est soit vraie, soit fausse (0 ou 1) et que, si elle n’est pas vraie, on peut être garant à coup sûr qu’elle est fausse (et vice versa).
La logique du flou consiste à ne pas se restreindre à ces deux possibilités et à adjoindre d'autres valeurs intermédiaires: un nombre réel compris entre 0 et 1.
– v. Logique floue, tiers exclu
– intérêt: automatique, robotique et divers domaines comme la médecine, le contrôle aérien, etc.
– a. Fuzzy logic: a form of many-valued logic in which the truth value of variables may be any real number between 0 and 1

Fluxion: nom que donnait Newton aux dérivées lorsqu'il les a inventées: "quotient ultime de deux accroissements évanescents". L'évêque Berkeley s'en moquait en les caractérisant de "fantômes de quantités disparues". Newton avait découvert le concept de limite.

Fonction: Règle ou loi qui définit les relations entre variables. Par exemple y = f(x), où pour chaque x il y a un y unique qui lui est associé.
Relation qui à un nombre (antécédent) en fait correspondre un autre (image) via une formule f.
Relation entre deux ensembles E et F qui, à tout élément de E, fait correspondre au plus un élément de F.
L'ensemble départ (ou source) E est le domaine de la fonction et l'ensemble d'arrivée (ou but) F, le codomaine.
– origine: C'est Dirichlet qui a proposé le concept moderne de fonction.
– ex. À vitesse constante, la distance parcourue est fonction du temps. Notation: d = f(t).
– notation avec une flèche.
– ex. Les fonctions et ;
f et g sont des polynômes.
– étym. Du latin functio, exécution, accomplissement.
– v. Vocabulaire des structures algébriques
– a. Function
– syn. Application (se dit: map en anglais), morphisme

Fonction booléenne: qui prend les valeurs vrai ou faux, souvent représentées par 1 ou 0 et parfois par 1 et -1.
Base de la réalisation de circuits logiques, comme les automates: un bit de sortie pour k bits en entrées ou plus généralement, un mot binaire comme fonction der k mots binaires.
– v. Logique
– a. Bolean function

Fonction de: si on donne un nom (y) au polynôme, et si on note ,
on dit que y varie en fonction de x.
– v. Fonction.
– a. y is a function of x

Fonction constante: du type .
Représentée par une droite verticale.

Fonction linéaire: du type .
Représentée par une droite oblique passant par l'origine.

Fonction affine: du type .
Représentée par une droite oblique.
La variation de la fonction est proportionnelle à celle de la variable.
– v. Affine
– a. Linear function

Fonction quadratique: du type ;
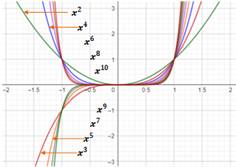C'est une fonction de plusieurs variables polynomiale de degré 2.
– v. Parabole, équation du second degré
– a. Quadratic function

Fonction puissance: du type .
(Illustration)
– v. Puissances
– a. Power functions

Fonction logarithme: du type.
– v. Logarithmes, fonction exponentielle
– a. Power functions

Fonction homographique: du type .
C'est le quotient de deux fonctions affines avec c non nul.
Sa représentation est une hyperbole équilatère.
Elle est propre si ad – bc n'est aps nul.
– a. Homographic function: the quotient of two first-degree polynomial functions,

Fonction circulaire ou fonctions trigonométriques: sinus, cosinus, tangente, cotangente, sécante, cosécante …
– v. Trigonométrie
– a. Trigonometric functions

Fonction circulaire réciproque: arcsinus, arccosinus, arctangente …
– v. Fonctions circulaires réciproques
– a. Inverse trigonometric functions

Fonction de répartition ou fonction de distribution cumulative: retourne la probabilité cumulée lorsque la variable est inférieure ou égale à une valeur donnée.
– v. Probabilités, densité de probabilité
– a. cumulative distribution function (CDF)

Fonction (informatique-script): groupement de plusieurs lignes d'instructions entre deux accolades qui définit les instructions associées à un terme (auquel on attribue le nom de la fonction). L'exécution consiste simplement à appeler cette fonction par son nom.
– syn. Procédure, routine, sous-programme.
– ex. Fonction en langage Python, exemple Python, procédure avec Maple
– v. POO – programmation orientée objet

Fonctionnelle (relation -): lorsque, pour tout élément x de E, x n’est en relation qu’avec 0 ou 1 élément y de F, on dit que la relation est fonctionnelle.

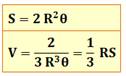for … anglais signifiant pour. En informatique, permet de débuter une exploration en boucle.
– ex. Sur l'lustration, traduire: pour k pour les valeurs successives 1, 2, 3, 7 faire: imprimer kn k², k³: fin de faire.
– v. Programmation des boucles

Force: c'est ce qui se passe lorsqu'on pousse un objet pour le déplacer, lorsqu'on tire sur la corde d'un arc pour le bander; la poussée de l'eau sur un barrage, etc.
Action mécanique exercée sur un objet par un autre objet ou par un champ.
Une force appliquée à un objet lui impose une accélération.
Le poids est une force.
– unité SI: newton de symbole N
– v. Résultante, unités de force, lois de Newton, poussée d'Archimède
– v. Forces, contrainte
– v. Force: a force can cause an object with mass to change its velocity, to accelerate.

Force: toute cause capable de déformer un corps, d'en modifier l'état de repos ou de mouvement. Une force s'exerce dans une direction, un sens et avec une certaine intensité. Elle est représentée par un vecteur.
Sans force appliquée, une voiture roulerait à vitesse constante (mouvement uniforme). En fait, il faut lui communiquer une force tout de même pour compenser la force de la résistance du vent et celle de frottement sur la route.
En appliquant une force à un mobile, on le met en mouvement accéléré.

Force brute: méthode qui consiste à tester systématiquement toutes les solutions d'un problème jusqu'à trouver la bonne.
Aussi nommée: recherche exhaustive.
Méthode adaptée aux recherches par ordinateurs.
– v. Parcimonie
– a. Brute force search, brut force algorithm.
Proof by exhaustion, proof by cases, proof by case analysis

Formalisme: ceux qui considèrent que les maths sont une construction intellectuelle, abstraite; et non pas le reflet du monde réel.
Utilisation d'un langage formel muni de règles de calcul ou de règles déductives.
– ex. Logique formelle.
Les maths utilisées comme outil de raisonnement.
– ex. Introduction des repères et des coordonnées en géométrie (géométrie analytique de Descartes).

Formel: la forme prime sur le fond.
– ex. En logique, une proposition est vraie si elle vérifie certaines propriétés logiques, peu importe sa signification.

Forme algébrique ou polynôme homogène: tous les termes (monômes) sont de même degré total (même somme des exposants).
– ex. x⁴ + x²y² + 3xy³– a. Homogeneous polynomial

Forme développée d'un polynôme: tous les calculs possibles sont effectués, développés.
– ex. 5(2x + 3) = 10x + 13
– a. Expanded polynomial

Forme développée d'un nombre: faisant apparaitre les puissances de 10.
– ex. 1234 = 1000 + 200 + 30 + 4 = 1 × 10³ + 2 × 10² + 3 × 10¹ + 4 × 10⁰
– a. Expanded form of a number

Forme factorisée: Toutes les possibilités de factorisation sont exploitées.
– ex. x² + ax + bx + ab = x(x + a) + b(x + a) = ((x +a) (x +b)
– a. Factored form: A fully factored form means the given number or polynomial is expressed as a product of the simplest possible form

Forme quadratique: polynôme homogène de degré 2.
– ex. x² + xy + 3y²– Appli. Crible d'Atkin, théorème des quinze
– v. Formes quadratiques
– a. Quadratic form

Forme quadratique binaire: polynôme de la forme: ax² + bxy + y².
– v. Quadratique binaire
– a. Binary quadratic form (BQF)

Forme (de même -): synonyme de égal, isométrique pour les figures géométriques.
– a. Same shape

Forme linéaire de logarithmes de nombres algébriques:
sous certaines conditions a log a' + b log b' + … est un nombre transcendant (théorème de Baker).

Formule: synonyme d'égalité (ou inégalité) pour calculer quelque chose.
Indique comment calculer une grandeur en fonction d'autres grandeurs.
– ex. La formule A = ½ a.h donne l'aire du triangle.
– v. Identités remarquables, formules de trigonométrie

Formule de Stirling* permet de calculer directement la valeur d'une factorielle.
– propriété: , d'autant plus exacte que n est grand.
– v. Formule de Stirling
– a. Stirling's approximation or Stirling's formula

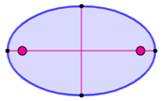
Foyer: autre nom pour une sorte de centre d'une figure (conique).
Suggère une notion de convergence de rayons vers les foyers.
– v. Ellipse, construction des foyers de l'ellipse
– a. Focus

Fractale* figure qui est semblable même en changeant l'échelle de vision de la figure.
Une figure fractale présente un caractère d'autosimilarité.
Sa dimension est exprimée par une fraction.

– ex. Pou de Mandelbrot, courbe de Koch ou flocon de neige,
– v. Fractales, chaos, complexité

"Le cœur même de la finance est fractal", affirme Benoît Mandelbrot, le grand mathématicien français, inventeur d'une branche des mathématiques avec les fractales; Rien ne ressemble plus à un cours de Bourse sur une journée qu'un cours sur une semaine, un mois, une année, et c'est précisément de cette façon que l'on identifie une fractale (une forme identique à des échelles différentes).

Fraction: l'analogie de la tarte est toujours pertinente: une fraction exprime la quantité N de parts prises dans une tarte coupée en D parts. On écrit cette opération: N / D.
– illustration: En haut, la tarte est découpée en quatre QUARTS. Le QUART devient notre unité de mesure, notée en abrégé: /4.
Ainsi, 1 QUART est noté 1/4; 3 QUARTS est noté 3/4.

Une fraction est composée de deux nombres:
    - l'unité de mesure (demi, quart, huitième, centième …, dénommée: dénominateur, et
   – la mesure (combien d'unités), nommée: numérateur.
– syn. Nombre rationnel.
– étym. Ce mot vient de la traduction d'un mot arabe qui signifie rompus, fracturé.
– v. Rapport, proportion, prorata, pourcentage
– v. Fraction, règle de trois, multiplication
– a. Fraction: a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, three-quarters. Fraction line (trait de fraction).

Fractions équivalentes: fractions dont les numérateurs et dénominateurs ont été multipliés par le même nombre
– ex. 1/2 = 2/4 = 4/8 = 50/100 = …
– a. Equivalent fraction

Fraction irréductible, minimale ou simplifiée: réduite à des nombres aussi petits que possible.
Numérateur et dénominateur n'ont plus aucun diviseur commun.
Fraction telle que numérateur et dénominateur sont premiers entre eux.
Il est d'usage de présenter la faction la plus simple, la fraction minimale.
– ex. 50/100 = 1/2, 37/111 = 1/3.
– v. Simplification des fractions
– a. It is usually best to show an answer using the simplest fraction (1/2 in this case ).
       That is called simplifying, or reducing the Fraction

Fraction impropre: dont le numérateur est plus grand que le dénominateur.
– ex.
– a. An improper fraction can be converted to a mixed number

Fraction à étage ou fraction composée: numérateur et ou dénominateur comportent des fractions.
– v. Fraction à étage, fraction continue, quotient de quotient
– a. Complex fraction or compound fraction are fractions in which either the numerator, denominator, or both contain fractions themselves.

Fraction décimale: le dénominateur est une puissance de 10.
– ex: 77/100 = 0,77
– a. Decimal fraction: 7/10 is a decimal fraction and it can be shown as 0.7.

Fraction dyadique: le dénominateur est une puissance de 2.

Fraction périodique: fraction dont le développement décimal est répétitif.
– ex. 1/ 7 = 0,142857 142857 …
– notation:      La partie périodique est surlignée.
La fraction périodique est simple si la période suit le 0 du début. Elle est mixte si une partie fixe précède la partie répétitive.
Trouver la période se dit: réaliser le développement décimal périodique de la fraction ou d'un nombre rationnel
– v. Fraction périodique
– a. A repeating decimal or recurring decimal is decimal representation of a number whose digits are periodic and the infinitely repeated portion is not zero.
– a. Repetend or reptend désignent la période.

Fraction continue: ou fraction à étages.
Manière d'exprimer un nombre réel, notamment irrationnel.
– ex. Illustration avec Pi et Phi (le nombre d'or)
– notation abrégée: π = [3; 7, 15, 292, …], ϕ = [1; 1, 1, 1, 1…]
– v. Quotient de quotient ou fraction à étages
– v. Fraction continue
– a. Continued fraction

Fraction unitaire et fraction égyptienne: dans les deux cas, le numérateur vaut 1, sauf quelques rares exceptions pour les égyptiennes.
– v. Fraction égyptienne
– a. Egyptian fraction

Fraction médiane: à partir de deux fractions, la fraction médiane est celle dont le numérateur est la somme des numérateurs et idem pour le dénominateur.
Avec 1/2 et 1/3, la fraction médiane est 2/5.
Propriété: la fraction médiane est toujours comprise entre les deux fractions-mères (0,333… < 0,4 < 0,5).
– a. The mediant of two fractions a/c and b/c is defined as: (a + b) / (c + d).

Fractions en lettres: les neuf lettres de fractions font l'objet d'un jeu pannumérique.

Fractionnaire (exposant): qui se présente sous la forme d'une fraction.
– ex. 5^1/2 = Ö5.
– note: l'expression nombre fractionnaire est abandonnée au profit de nombre rationnel.
– v. Exposants fractionnaires
– a. Roots can also be defined as special cases of exponentiation, where the exponent is a fraction

Fractionnaire (partie -): la partie fractionnaire (ou décimale) de 12,34 est 34, soit la partie exprimée par les décimales; 12 étant la partie entière.
– a. Fractional part or decimal part: the fractional part corresponds to the digits appearing after the radix point.

Nombre fractionnaire: nombre qui contient une partie entière et une partie fractionnaire.
Autrefois appelé: nombre mixte.
– ex. 3 ½ qui signifie 3 + ½ = 7/2. La fraction 7/2 est dite impropre
– a. mixed number (3 ½), improper fraction (7/2)

Fréquence: nombre de périodes par seconde pour une fonction périodique.
Elle est mesurée en hertz (Hz).
– ex. Je tape mon poing sur la table toute les secondes, la fréquence est de 1 Hz.
– v. Octave, quinte, quarte
– v. Hertz, échelle des fréquences, ondes
– a. Frequency

Fréquence d'un caractère: nombre de fois que le caractère quantitatif ou variable quantitative) prend une valeur donnée divisé par la quantité totales des cas.
Quotient de l'effectif du caractère (de la valeur) sur l'effectif total.
– ex. Sur 20 hommes, 4 mesurent 1,73 m, alors, la fréquence du caractère "hommes de 1,73 m" = 4/20 = 0,2.
Pour une modalité (valeur) d'un caractère, la fréquence est le rapport entre l'effectif de la modalité et l'effectif total.
Cette fréquence est souvent exprimée en pourcentage.
– v. Caractère
– v. Statistique, probabilités et statistiques

Fréquence cumulée d'un caractère: Quotient de l'effectif cumulé sur l'effectif total.

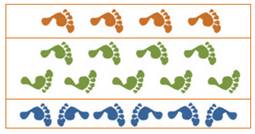Frise: dessin répétitif, dit motif, à l'intérieur d'une bande continue.
Il existe seulement 7 possibilités de répéter ce motif par transformation isométriques.
En maths, les frises forment un groupe.
– syn. Maillage
– v. Frise
– a. Frieze, frieze pattern, frieze group

Frontière: ligne fermée qui sépare une région entre intérieur et extérieur.
Aussi, ligne qui définit un demi-plan.
– syn. pourtour, contour, périmètre
– ex. La frontière du disque est un cercle appelé périmètre. La sphère est la frontière de la boule.
– a. Boundary, A disk is said to be closed if it contains the circle that constitutes its boundary, and open if it does not

Frustum: anglais pour tronc de cône ou de pyramide.
– a. A pyramid or cone with the top cut off flat. Can be any part of a solid between two parallel planes.

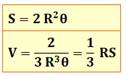Fuseau sphérique: partie de la sphère semblable à un quartier d'orange.
Surface sur la sphère limitée par deux demi grands cercles
L'onglet sphérique est le volume associé au fuseau.
– v. Sphère, sphère terrestre
– a. Spherical lune, biangle, spherical wedge (pour l'onglet).

>>> G

Voir	Atlas des maths – des références Débutants – pour juniors ou novices
Aussi	DicoNombre – tous les nombres de 0 à l'infini DicoLettre – signification des lettres en maths et ailleurs DicoCulture lettre F
Autres	Voir page des liens et références
Cette page	http://villemin.gerard.free.fr/Referenc/Encyclop/F.htm