|
|
Ce
site est désormais accessible en http://diconombre.fr/index.html et pour cette page voir
le lien en fin de page For
this page, refer to the link at the bottom. |
|
22 Novembre
2025
|
Édition du: 08/04/2026 |
|
INDEX |
Topologie |
||
|
Problème du rectangle inscrit Problème du carré inscrit –
Conjecture de Toeplitz Une conjecture
simple à énoncer: on peut inscrire un carré ou un rectangle sur toute courbe
fermée continue et lisse. Le cas du carré est
toujours une conjecture ouverte. Le cas du rectangle a été
résolu en 2020. La
démonstration est originale. Elle procède en plusieurs étapes dont une qui
fait appel à la topologie.
|
||
|
|
Sommaire de cette page >>> Problème du rectangle inscrit >>> Cas des courbes simples >>> Principe de la démonstration pour le
rectangle >>> Bilan et extrait de la démo complète >>> Historique |
Débutants Glossaire |
Anglais: The inscribed square problem
/ The rectangular peg problem / Toeplitz’s square peg conjecture
|
|
||
|
Résolution en 2020 Le problème
du rectangle inscrit est un vieux
problème qui vient d'être résolu pendant le confinement du printemps 2020 par
Joshua Greene et Andrew Lobb. Une première
avancée avait été faite vers la fin
des années 1970 par Herbert Vaughan. |
Origine C'est Ott Toeplitz, un
mathématicien allemand qui formule cette conjecture en 1911. Sa conjecture
s'appliquait au carré, cas toujours non résolu. Malgré sa formulation
simple, de nombreux mathématiciens s'y sont cassé les dents. Comment appliquer les
propriétés du carré sur les points d'une courbe quelconque ? |
|
|
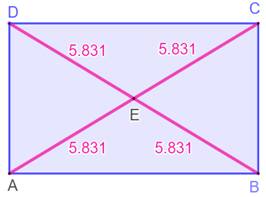
Théorème Toute courbe fermée contient au moins un quadruplet
de points qui forme un rectangle. Pour toute courbe lisse
de Jordan (courbe simple) et tout rectangle R dans le plan euclidien, il
existe un rectangle similaire à R dont les sommets sont sur la courbe.
|
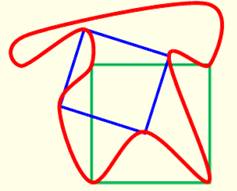
Exemple
Sur la courbe rouge, on
a été capable d'y inscrire au moins un carré. Est-ce toujours faisable ? |
|
Voir Brève 59-1178
|
|
||
|
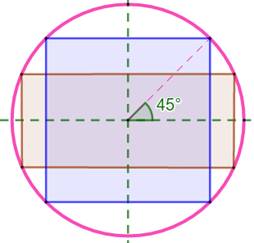
Cercle Le carré est
inscriptible dans le cercle et de
multiples façons par rotation. Le rectangle
l'est également de multiples façons par rotation est aussi par changement de
taille. Avec deux
points sur la circonférence, il est toujours possible de construire un
rectangle inscrit. |
|
|
|
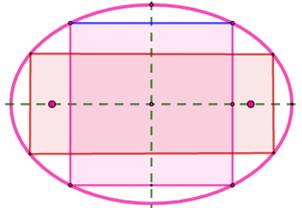
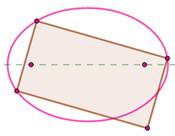
Ellipse Le carré est
inscriptible dans l'ellipse
d'une seule façon et son côté est fonction des
mesures des axes de l'ellipse. Le rectangle
inscrit a des côtés parallèles aux
axes. Il y en a une infinité. Note: impossible
d'inscrire un rectangle en oblique. |
|
|
|
Conclusion Pour ses deux courbes symétriques fermées, la conjecture
est vérifiée. |
||
|
|
||
|
Description intuitive de la démonstration La
démonstration procède en plusieurs étapes et plusieurs mondes mathématiques. Voici une explication imagée. La traduction
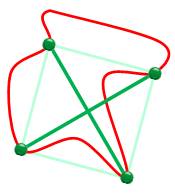
mathématique n'est accessible qu'à des experts du domaine (Voir le texte des auteurs).
Étape 1: diagonales Plutôt qu'au
rectangle, on va s'intéresser aux deux diagonales: elles ont mêmes mesures et
elles se coupent en leur milieu. Le principe
consiste alors à faire courir deux segments sur la courbe et à détecter les
cas d'égalité avec intersection au milieu. |
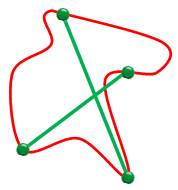
Diagonales égales
Critères satisfaits et Non respectés
|
|
|
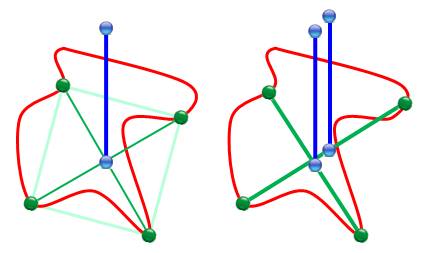
Étape 2: hauteurs Astuce !
Dresser une perpendiculaire au milieu de chacun des segments et lui donner la
longueur du segment (bleu). On obtient
une figure dans l'espace (en 3D). Il suffit
désormais de balayer la courbe et de détecter des hauteurs identiques (à
gauche) et de rejeter tous les autres cas (à droite). |
Traits bleus confondus = présence d'un rectangle
|
|
|
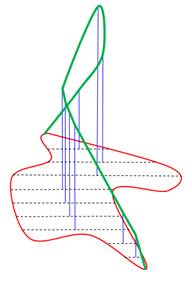
Étape 3: surface En balayant
tous les couples de points, on crée un ensemble de points, lieu des sommets
des hauteurs. La courbe
verte est un échantillon. Avec tous les points, la courbe se transforme en
une surface qui enveloppe complètement la courbe. Cette surface est continue.
Une petite variation sur les points entraine un petit déplacement sur la
surface. Les points
où les hauteurs sont égales sont des points singuliers de la surface; des
points atteints par deux routes différentes; la surface se coupe elle-même. Comment
détecter ces singularités ? |
Lieu de l'extrémité de la hauteur
|
|
Vidéo
|
Même sans connaitre l'anglais, je vous
propose de visionner la vidéo du site: New
Geometric Perspective Cracks Old Problem About Rectangles – Kevin Harnett. Vous y retrouverez les figures de
cette page avec des animations. Les images 3D de cette page sont
extraites de cette vidéo. |
|
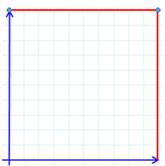
Étape 4: projection C'est ici
qu'intervient les techniques de la topologie. On coupe la
courbe et on la "pose" sur l'axe des x pour y faire courir un des
points de la paire (bleu). On fait courir l'autre sur l'axe des y (bleu). Une
paire de points devient une paire de nombres (de coordonnées) et donc, un
point désigné dans le plan. Attention,
on a artificiellement coupé la courbe; il faut penser à la reconnecter en
"enroulant" les axes (traits rouges). Oui, on obtient un tore
! |
La courbe transformée
Chaque point du plan
comme chaque point de la surface du tore représente une paire de points sur
la courbe initiale. |
|
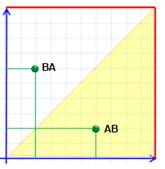
Étape 5: correction Nous sommes
allés un peu vite ! Une paire AB
représente deux segments AB et BA. Il ne faut en retenir qu'un seul. Sur le plan,
ces deux segments sont représentés par deux points symétriques par rapport à
la diagonale. Conséquence:
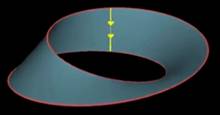
il ne faut garder qu'une moitié du plan (partie jaune). Une
opération de recomposition des bords conduit à abandonner le tore et à passer à un ruban de Möbius. |
Seule une moitié du plan
doit être conservée, alors chaque point de la surface du ruban représente une
paire ordonnée de points
de la courbe initiale. La bordure du ruban
correspond aux paires de points confondus sur la courbe initiale. |
|
Étape 6: la solution ! Si on
rapproche la surface "des hauteurs" et le ruban de Möbius:
Il est impossible d'appliquer le bord du
ruban sur la courbe (rouge sur rouge) sans forcer le ruban à se croiser. Et
le croisement est la singularité que nous cherchons. Donc: il
existe un endroit où la surface se recoupe et ce fait entraine que deux
diagonales égales se coupent en leur milieu et par conséquent un rectangle
existe quelque part. Note: la démonstration complète fait intervenir une surface à quatre dimensions:
la quatrième étant l'angle d'orientation des diagonales >>> |
Chaque point sur la
surface comme chaque point du ruban correspond à une paire de points sur la
courbe initiale. Imposer la superposition
topologique des deux figures entraine un croisement obligatoire, lequel est
le témoin de la présence d'un rectangle. |
|
Une
démonstration très sophistiquée mathématiquement mais qui dans son principe
expose une méthode originale et émouvante pour un amateur de mathématiques. |
Une idée du niveau mathématique nécessaire pour aborder la
démonstration complète
Extrait de: The Rectangular
Peg Problem – Joshua Evan
Greene, Andrew Lobb – Cornell University – 19 May
2020
L'historique
suivant est établit d'après ce même site
|
1911 – Toeplitz
– Formule la conjecture du carré inscrit. 1913 – Emch – Résoud
la conjecture pour des courbes lisses convexes. 1929 – Schnirelman
– Traite le cas des courbes lisses de Jordan mais avec une hypothèse qui ne
couvre pas tous les cas. 1981 – Vaughan – Avancée sérieuse dans
le cas des rectangles. Il introduit l'idée de s'intéresser au
lieu des hauteurs représentant les diagonales. Ce lieu contient
obligatoirement un point de triple intersection (auto-intersection) témoin de
la présence d'un rectangle. Le ruban de Möbius est déjà utilisé. 1991 – Griffiths – Croit détenir une
preuve pour le cas du rectangle; infirmée en 2008 par Matschke. 2018 – Hugelmeyer
– Réussit à résoudre quelques cas complémentaires selon l'angle des
diagonales (angle d'aspect) en recourant à la quatrième dimension. Lui aussi,
fait intervenir le ruban de Möbius pour conclure. 2020 – Joshua Evan
Greene et Andrew Lobb – Démonstration du théorème du rectangle inscrit en
prolongeant les travaux de Vaughan et en s'appuyant sur la nouvelle idée de
Huglemeyer pour analyser le ruban de Möbius: comment implanter
(typologiquement) le ruban de Möbius (2D) dans un objet à quatre dimensions ?
Il faut, en quelque sorte, donner à chaque point du ruban, une adresse à
quatre nombres:
Green et Lobb avaient déjà démontré
qu’il était possible d’intégrer la bande de Möbius dans un espace
(symplectique) à quatre dimensions d’une manière qui respecte les règles de
l’espace. Ce qu'ils voulaient vraiment savoir, c'était si chaque rotation de
la bande de Möbius croise la copie originale. En fait, deux bandes de Möbius qui se
croisent sont équivalentes à une bouteille de Klein, qui se croise dans ce
type d'espace. Et si vous faites pivoter une bande Möbius de sorte que la
copie pivotée ne coupe pas la copie originale, vous avez essentiellement
produit une bouteille de Klein qui ne se coupe pas. Mais une telle bouteille de Klein est
impossible dans un espace symplectique à quatre dimensions. Par conséquent,
chaque rotation possible de la bande de Möbius intégrée doit également se
croiser, ce qui signifie que chaque courbe fermée et lisse doit contenir des
ensembles de quatre points qui peuvent être réunis pour former des rectangles
de tous les rapports d'aspect. |
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
