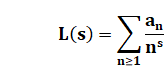|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Le programme de LANGLANDS La correspondance de Langlands Les conjectures de Langlands Le plus
important des concepts mathématiques des dernières décennies. Inutile de dire
que ce concept est hors de portée de la majorité d'entre nous, sauf à être
titulaire d'un bon bagage supérieur en mathématiques. Un des
mathématiciens participant à ce programme, Edward Frenkel, s'est pourtant
livré à un exercice de vulgarisation dans son livre Amour et Maths. Il faut néanmoins
bien s'accrocher! |
Le programme Langlands en bref
|
Le programme de Langlands est un
projet ambitieux qui a connu de multiples succès depuis sa première
formulation en 1967. Il s’agit d’un ensemble de conjectures dont
En 2024, avec la résolution du volet géométrique, les trois volets sont résolus. Ce projet, en plus de révéler des structures profondes au cœur des mathématiques, permet d’établir une sorte de dictionnaire qui traduirait un problème difficile en un autre plus simple. Par exemple en reformulant une question de théorie des nombres avec les outils de l’analyse. Un espoir pour démontrer des théorèmes récalcitrants ! |
Quelques mathématiciens du programme
Langlands
|
Robert Langlands a reçu le prix Abel en 2018 pour ses travaux sur le
programme mathématique qui porte son nom. |
|
André Weil (1906-1998),
mathématicien français de l'Institute for Advanced Study de Princeton (proche
de New-York) est l'un des grands noms de la théorie des nombres et de la
géométrie algébrique. Travaux sur la conjecture
de Riemann. Un des membres fondateur du groupe Bourbaki. Travaux sur la fameuse conjecture Shimura-Taniyama-Weil,
celle-ci, qui a été prouvée dans son intégralité en 1999, peut être
considérée comme l'un des éléments du programme de Langlands. |
|
En 2002, le mathématicien
français Laurent Lafforgue (né en 1966) a
reçu la médaille
Fields en 2002 pour avoir démontré une partie des conjectures de
Langlands. En 2000, après un passage au
CNRS, il est professeur de mathématiques à l'Institut des hautes études
scientifiques (IHÉS). |
|
Ses travaux sur l'algèbre
affine de Kac-Moody, lui offriront l'occasion de participer au programme de
Robert Langlands. Il se fera remarqué pour
avoir tatoué la formule de l'amour sur le corps de sa compagne. Son livre est lisible et très instructif ! |
|
En 2010, Ngo Bao Chau, mathématicien français né en 1972
au Vietnam, travaille sur le programme de Langlands. Médaille Fields en 2010. D'abord au CNRS, puis à
l'université de Paris 13 (Labo LAGA), il rejoint Princeton en 2007, puis
l'université de Chigago en 2010. En 2004, Gérard Laumon et
lui démontrent le lemme fondamental du programme de
Langlands |
Voir Contemporains
|
Connexions
entre domaines mathématiques |
|
|
|
L'analyse mathématique est un domaine des mathématiques
qui est consacré aux calculs exacts de systèmes compliqués en traitant de
très petites quantités. La trigonométrie utilise ces techniques pour
définir les relations entre les angles de figures géométriques. Les
fonctions trigonométriques (sinus et cosinus) sont aussi utilisées pour
décrire des phénomènes ondulatoires. L'étude
des ondes et leur décomposition en tranches de fréquence s'appelle l'analyse harmonique (comme les harmoniques d'un
son). L'outil adéquate s'appelle la transformée de Fourier. |
La théorie des nombres qui traite de relations
entre les nombres entiers. L'exemple typique étant la démonstration du
théorème de Fermat-Wiles. La
résolution générale des équations a conduit Galois à lancer la notion de
groupe et de symétries. La symétrie caractérise un objet dont les
propriétés sont conservées suite à un mouvement dans l'espace ou dans le
temps. Un groupe rassemble des éléments qui partagent tous
les mêmes propriétés de symétrie, les mêmes quel que soit l'ensemble
d'éléments. |
|
|
Le programme de Langlands tente de mettre en évidente des propriétés
mathématiques communes à tous ces domaines; à établir un pont entre la
théorie des nombres et l'analyse harmonique; de réaliser une grande théorie
d'unification des domaines mathématiques. Son ambition est de mettre au jour les relations complexes entre la
théorie des nombres, la géométrie algébrique et la théorie des
représentations de certains groupes |
||
|
|
||
|
Le plus important concept des mathématiques qui est apparu dans ces cinquante dernières
années: la Grande Théorie d'Unification
des mathématiques. Ce champ de recherche fascinant jette des ponts
prometteurs entre des domaines mathématiques qui paraissent à des
années-lumière les uns des autres: algèbre, géométrie, théorie des nombres,
analyse et physique quantique. –Edward Frenkel |
Expliquer ce qu’est le programme de Langlands n’est pas chose facile. Celui-ci mélange
l’analyse harmonique sur les groupes topologiques non commutatifs,
l’arithmétique des groupes de Galois de corps de nombres et la géométrie
arithmétique. Très
concrètement, il s’agit de comprendre certaines séries génératrices de la
forme:
|
|
|
Le programme de Langlands
fait référence à un ensemble surprenant de comportements mathématiques
existant en théorie des nombres et que 'on retrouve en analyse harmonique. Formulé
sous forme de conjectures,
les preuves sont plus difficiles à trouver qu'envisagé par Langlands.
Néanmoins certaines parties sont prouvées, comme celle démontrée par Laurent
Lafforgue en 2002. En 2004, Ngo Bao Chau et Gérard Laumon démontrent le lemme
fondamental. Celui-ci stipule que certaines intégrales associées à deux types
différents d'intégration dans deux groupes sont équivalents. |
||
|
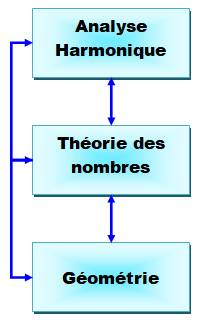
Analyse harmonique / Théorie des nombres / Géométrie |
|
|
|
Le
Programme de Langlands conjecture
l'existence de liens très profonds entre plusieurs domaines fondamentaux des
mathématiques, notamment:
via notamment les travaux sur la théorie de la résolution des
équations algébriques prenant naissance dans les travaux sur les groupes de
Galois.
qui consiste à s'intéresser aux phénomènes ondulatoires (ondes
lumineuses, gravitationnelles, ou sonores) en les "dépliant" dans le
domaine fréquentiel grâce aux séries ou transformées
de Fourier. Dans le cas du programme de Langlands, c'est une branche bien
particulière de l'analyse harmonique qui intervient et qui fait intervenir
les équations différentielles, les fonctions fuchsiennes et les formes
automorphes.
qui, notamment, identifie a symétrie caractérisant un objet dont les
propriétés sont conservées suite à un mouvement dans l'espace ou dans le
temps. |
Image par Sandro
Contenta: s'il est possible de prédire le son émit par un tambour d'après
sa forme, il est aussi possible de prédire la forme du tambour d'après les
sons émis. Idée de propriétés partagées dans un cas comme dans l'autre. |
|
Voir Brève 61-1200
|
Analogie
|
|
|
|
Vous
connaissez peut-être l'analyse
de Fourier En analyse de Fourier classique, une procédure appelée
transformée de Fourier crée une correspondance entre deux manières
différentes d'appréhender le graphe d'une onde (comme une onde sonore).
La
transformée de Fourier effectue des allers-retours entre ces
deux visions.
La
capacité à franchir cette frontière est essentielle à de nombreuses
applications. Sans
elle, nous n'aurions pas les télécommunications modernes, le traitement du
signal, l'imagerie par résonance magnétique, ni de nombreux autres éléments
essentiels de la vie moderne. |
Le programme de
Langlands propose quelque chose de similaire
mais avec des ondes et des fréquences plus sophistiquées. Exemple Ondes sinusoïdales => fonctions propres (Eigenvalue).
Alors que la fréquence d'une onde sinusoïdale est un nombre unique, celle
d'une fonction propre est une liste infinie de nombres. Spectre => ensemble d'objets de la théorie des
nombres qui, selon Langlands, étiquettent le spectre de fréquences des
fonctions propres. De manière assez inattendue, une procédure proche
de la transformée de Fourier relie le côté onde et le côté spectral. Les ondes et leurs étiquettes de fréquence
proviennent de domaines mathématiques très différents, de sorte que la
correspondance entre elles, lorsqu'elle peut être prouvée, est souvent riche
en renseignements. Par exemple, une preuve de la correspondance de
Langlands de la théorie des nombres pour un ensemble relativement petit de
fonctions dans les années 1990 a permis à Andrew
Wiles et Richard Taylor de prouver le dernier théorème de Fermat, qui a
été pendant trois siècles l’une des questions ouvertes les plus célèbres des
mathématiques. |
|
|
Depuis des décennies, des mathématiciens du monde
entier travaillent sur le programme de Langlands, un vaste projet
d’unification des mathématiques. Une démonstration de plus de 1000 pages résout
aujourd’hui (mai 2024) le volet géométrique, ouvrant de nouvelles
perspectives en mathématiques. |
En mai 2024, neuf mathématiciens ont publié un
ensemble de cinq articles, couvrant près de 1 000 pages, établissant la
preuve du programme de Langlands géométrique. Ils sont parvenus à relier deux continents des
mathématiques : la théorie des nombres et la géométrie. |
|
|
Dennis Gaitsgory (à gauche) et Sam Raskin, les
leaders de l'équipe des neufs mathématiciens. |
|
|
![]()
|
Dans le monde
mathématique classique, disons du lycée, on connait les nombres en arithmétique et les fonctions en algèbre. |
Dans le monde
de Langlands, disons le monde des structures
sophistiquées, au lieu de nombres, on parlera d'espaces
vectoriels et au lieu de fonction, on parlera de faisceaux. |
|
|
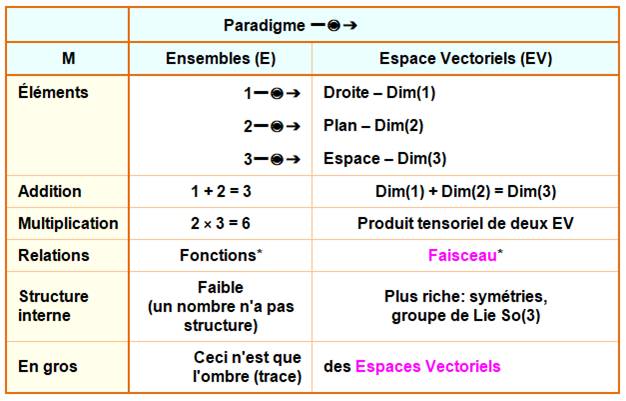
D'un monde à l'autre Imaginons un monde dans lequel les entiers
naturels sont remplacés par des espaces
vectoriels: la droite remplace le nombre1, le plan remplace le nombre 2,
et ainsi de suite. Les entiers forment un ensemble; les espaces vectoriels
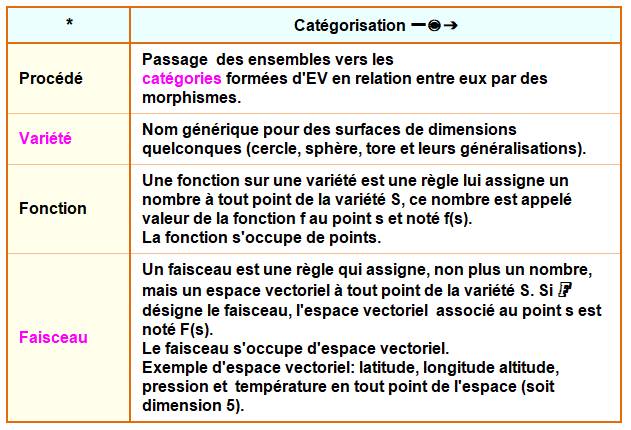
(EV) forment une structure plus sophistiquée que les mathématiciens appellent
une catégorie. Une catégorie comprend des objets (comme des EV) et des morphismes
(relations particulières comme la symétrie) entre ces objets. Bref aperçu du vocabulaire et des
concepts
|
||
D'après le livre d'Edward Frenkel – Pages 200 à 203
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Sites |
|
|
Cette page |