NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/01/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres – Motifs
Débutants Nombres figurés	NOMBRES CARRÉS			Glossaire Nombres carrés
INDEX Carrés Nombres figurés Feuille de route	Introduction	Caractérisation	Carrément carré	Doublement carré
	Car = Car × Car	CatCar	Carré-carré	Doublement cube
				Chiffres des carrés
		Sommaire de cette page >>> Caractéristiques >>> Liste de tout type >>> Liste stricte >>> Cas de récurrence avec 4 et 9 >>> Carré concaténation de trois carrés >>> Carré et concaténations de cubes >>> Cube et concaténation de carrés >>> Bilan >>> Anglais

NOMBRES carrément carrés

Il existe une grande variété de motifs faisant intervenir la concaténation avec des carrés. Ces pages en présentent quatre types:

Carrément carré (Nombres) 144 400 = 380² & 144 = 12², 400 = 20²	Carré-carré 49= 7² & 2² = 4, 3² = 9
Doublement carré (Chiffres) 169 = 13² & 1 + 6 + 9 = 16 = 4²	Catcar (concaténation et carrés) 88² + 33² = 8833

Il n'existe pas de noms avérés, en français comme en anglais, pour ces variétés de nombres.

Caractéristiques
Famille	Nombre / Figuré / Carré
Définitions	NOMBRE carrément CARRÉ Nombre carré Formé de deux carrés concaténés (accolés).
Formule	avec A = a² & B = b²
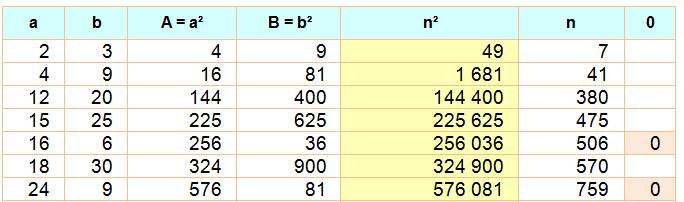
Exemple	144 400 = 380² 144 = 12² & 400 = 20²
Cousins	Les nombres carré-carré sont des carrés dont chaque chiffre est un carré. Ex: 49 = 7² et 4 = 2², 9 = 3². En plus, celui-ci semble être l'unique tel nombre formé de deux carrés consécutifs. Les nombres doublement carré sont des carrés dont la somme des chiffres est un carré. 81 = 9² et 8 + 1= 9 = 3². Note: ce vocabulaire n'est pas stabilisé!
Propriétés	Il existe une infinité de nombres carrément carré. Le plus petit est 49 avec 49 = 7² & 4 = 2², 9 = 3². Variétés de nombres carrément carré 169 = 13² quantité quelconque pour chaque partie concaténée (CC); 1681 = 41² même nombre de chiffres pour chaque partie, symétrie (CCS); 256 036 = 506² symétrique avec autorisation de 0 intermédiaires pour donner autant de chiffres au carré de droite qu'à celui de gauche (CCS0). Note: Sont exclus les nombres avec un deuxième carré en 00, comme 1 600 ou 2 500 …
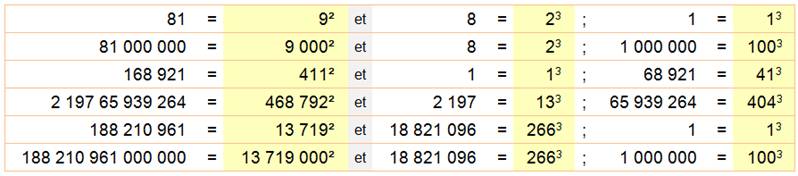
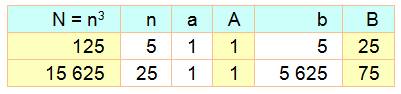
Extension	Cette page s'intéresse également au carrés, cubes et bicarrés qui sont la concaténation de deux ou trois carrés ou cubes. Voir bilan.

Liste des nombres carrément carré CC et CCS
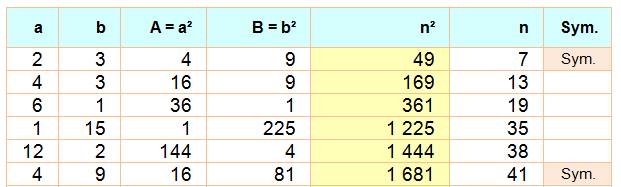
Il y en a 35 pour a et b jusqu'à 100. Suite >>>

Liste des nombres carrément carré CCS et CCS0
Il y en a 47 pour a et b jusqu'à 10 000. Suite >>>

Cas récurrent en 4 et 9
Explication avec l'exemple 49 et 99

Voir Identités remarquables / Motifs avec nombres

Carré et concaténation de trois carrés
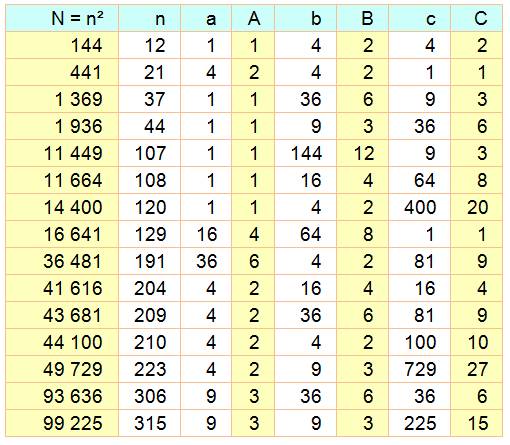
Ils sont relativement nombreux Exemple: 144 = 12² et 1 = 1², 4 = 2² 1 936 = 37 et 1 = 1² , 9 = 3² , 36 = 6². Remarquez les couples de mêmes chiffres: 144 et 441; 1 369 et 1 936; 11 664 et 16 641. Remarquez le couple de nombres successifs: 107² et 108².

Carré et concaténation de cubes
Nombre carré formé de la concaténation de deux cubes Testé jusqu'à N = 10^18 Nombre carré formé de la concaténation de trois cubes Testé jusqu'à N = 10^18

CUBE et concaténation de carrés
Nombre cube formé de la concaténation de deux carrés. Testé jusqu'à N = 10^13 Nombre cube formé de la concaténation de trois carrés Testé jusqu'à N = 10^18

Bilan

Carrés ou cubes comme concaténation de deux ou trois carrés ou de cubes

	2 carrés	3 carrés	2 cubes	3 cubes
Carré
	>>>	>>>	>>>	>>>
Cube			Aucun pour N < 10^18	Aucun pour N < 10^18
	>>>	>>>
Bicarré	Aucun pour N < 10^12			Aucun pour N < 10^18

English corner
49, 1681, 144 400: Squares with an even number of digits, where the first half is a square and the second half is a non-zero square. For example: 1681 is a square, where the first two digits form a square and the last two digits form a nonzero square. A funny square is formed by concatenating two consecutive squares. 49 is the only known funny square?

Suite	Nombres doublement carré Nombres doublement cubes Nombres consécutifs concaténés – Nombres de Sastry Palindromes et nombres concaténés
Voir	Nombres carrés – Glossaire Nombres carrés – Index Puissances somme de puissances
Site	Nombre carrément carré – Wikipédia OEIS A145848 - Squares with an even number of digits, where the first half is a square and the second half is a nonzero square OEIS A147608 - Squares which are concatenation of two positive squares with possible intervening zeros OEIS A039686 - Squares which are the concatenation of two nonzero squares
Cette page	http://villemin.gerard.free.fr/aNombre/FIGURE/CarCar.htm