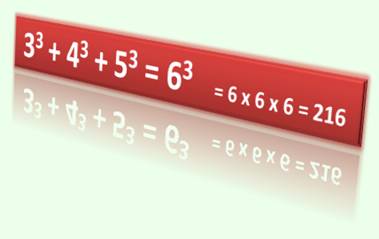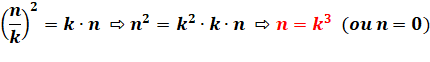|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
Humour

Voir Humour Source images Envision sur
une idée de Joyreactor
|
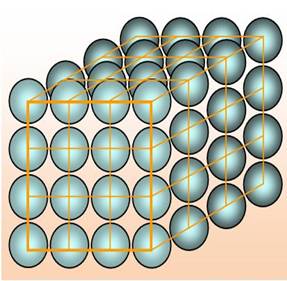
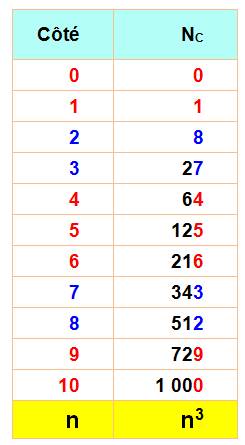
NOMBRES CUBES Nombres géométriques à la puissance trois. Un cube est un nombre multiplié trois fois par
lui-même. Notation: n3. Ex: 103 = 10 x 10 x 10 = 1000 53
= 5 x 5 x
5 = 125 |
|
|
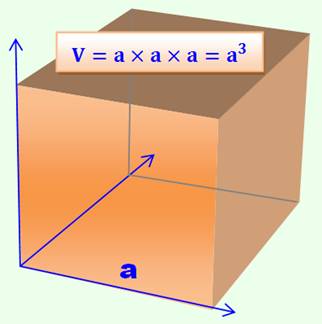
Volume d'un cube
|
Perfection cubique!
27 + 64 +
125 = 216 |
Voir Cubes en géométrie / Formule de perfection cubique / Pépites
|
Égalité Seuls
trois nombres sont égaux à leur cube:
Nombre et son cube Un nombre
diffère de son cube par un multiple de 6. C'est le cas
pour toutes les puissances impaires. Une
application inattendue des identités
remarquables. En effet: n3 – n = n (n2
– 1) = n (n – 1) (n + 1) = (n – 1) n (n + 1) Le
cube diminué du nombre est égal au produit de ce nombre par ses deux voisins.
C'est surtout le produit de trois nombres consécutifs. Parmi
eux, il s'en trouve toujours au moins un divisible par 2 et un divisible par
3. Le produit
est divisible par 6. Exemples 23 – 2 = 6 103
– 10 = 990 = 6 x 165 123
– 12 = 1 728 – 12 = 1 716 = 6 x 286 25 – 2 = 30 = 6 x 5 107
– 7 = 9 999 990 = 6 x 1 666 665 Exemple de calcul mental de cube 113
= 10 x 11 x 12 + 11 = 1320 + 11 = 1331 À noter aussi cette autre affinité avec le nombre 6:
La différence
troisième des cubes est égale à 6. Parité Un
nombre et ses puissances sont de même parité. Suite
>>> Divisibilité Le cube d'un
nombre n, augmenté d'une unité, est divisible
par n + 1. Justification: n3 + 1 = (n + 1)
(n² – n + 1) Exemple: 8 + 1 = 23
+ 1 = 3 x (4 – 2 + 1) = 3 x 3 Applications
"remarquées" des identités
remarquables La
différence entre deux cubes successifs (+n1) et n est égale à la somme de
nombres successifs jusqu'à 3n + 1, en retirant
les multiples de 3.
Voir Application avec le crible de
Moessner L'identité indiquée est la suivante:
(n+1)3 – n3 = n3 + n(n+1) + (n+1)3
= 3n² + 3n + 1 La
somme
partielle, déduite des multiples de 3, conduit au même résultat:
|
Voir Nombres de Lucas-Carmichael
|
|
||
|
4 x 4 x 4 = 43 = 4 x 16 = 64 |
|
|
|
Suite
>>> Idée de dénombrement Il
y a quatre cubes inférieurs à 100 et la somme
de deux d'entre eux est toujours inférieure à 100, sauf pour 43 +
43 = 64 + 64 = 128. En
prenant deux carrés parmi 4, on trouve la quantité de sommes possibles
inférieures à 100, à condition de lui retirer un.
Ce
sont: 2, 9, 28, 65, 16, 35, 72, 54, 91. Avec
500, il y a 7 cubes et deux sommes qui
dépassent 500 (63 + 73 = 559 et 73 + 73
= 686)
Avec
1000, on trouverait : 41, avec 14
débordements. |
|
|
Voir
Calcul
mental de la racine cubique / Dénombrements
(p-suite)
|
Énigme Quel
est le nombre dont le carré du tiers est égal au triple du nombre ? C'est
27, car (27/3)2 = 81 et 3 x 27 =
81. Notez que 27 = 33. Solution générale
|
|
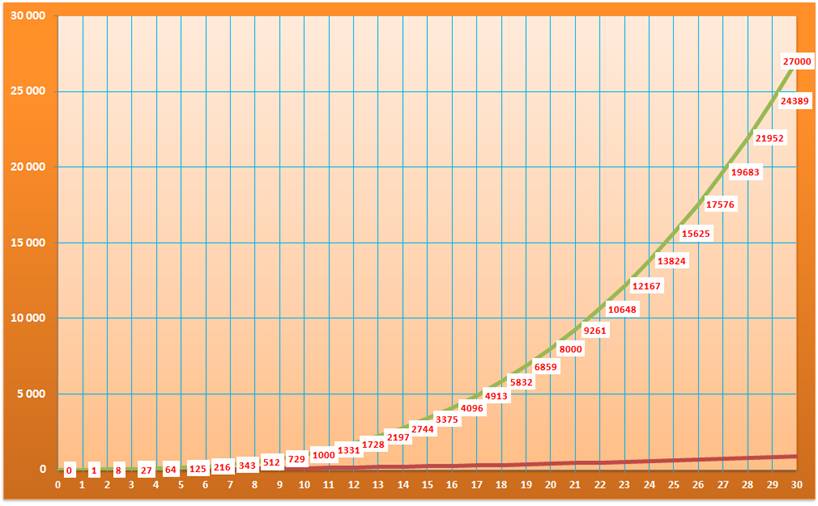
Courbe présentant la vitesse
d'évolution comparée des carrés (rouge) et des cubes (vert):
|
Voir Table
des cubes et somme de cubes
|
|
||
|
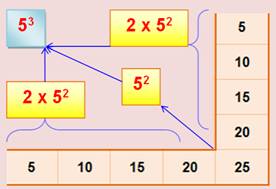
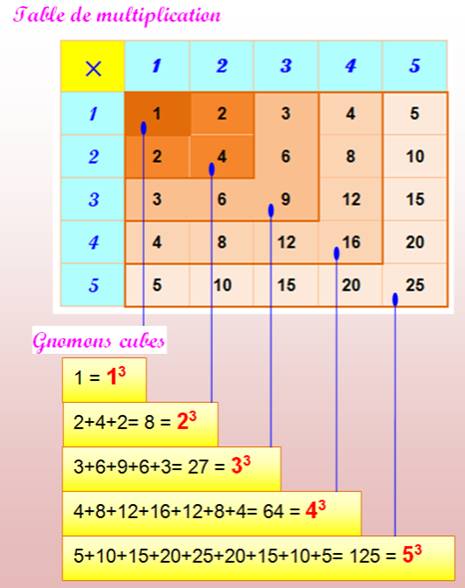
Table de
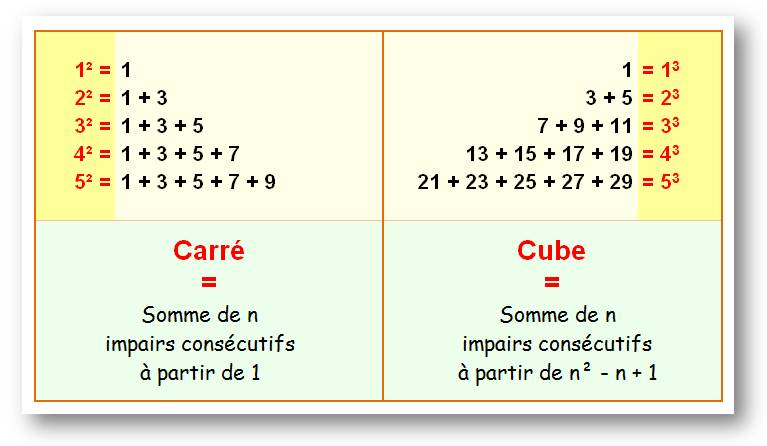
multiplication On peut trouver les cubes Exemple: 23 = 2 + 4 + 2 = 8 Ils se nichent dans une équerre, Remarquez la symétrie des calculs
des cubes dans les gnomons.
|
|
|
Voir Identité impair, carré et cubes / Somme des impairs
|
Somme
des cubes
Propriété
surprenante qui est en fait générale Voir Phénoménal
100
Les cubes sont aussi somme
des nombres hexagonaux centrés successifs n3 = 1 + 7 + 19 + … + Hcn-1 + Hcn |
Voir Démonstration / Triangulaires
(Tn) / Somme des cubes
en trois / Différence entre carrés
|
Trucs de calcul rapide |
|
|
|
Un nombre (n + 1)3
= n3 + 3n2 + 3n + 1 (n – 1)3
= n3 – 3n2 + 3n – 1 |
33 = (2 + 1)3 = 23 + 3x22
+ 3x2 + 1 = 8 + 12 +
6 + 1 = 27 93 = (10 – 1)3
= 103 – 3x102 + 3x10 – 1 = 1000
– 300 + 30 – 1 = 729 |
|
|
Deux nombres (n + 1)3
+ n3 = 2n3 + 3n2 + 3n + 1 (n + 1)3
– n3 = 3n2 + 3n + 1 |
43 + 33 = 2x27 + 3x9 + 3x3 + 1 = 54 + 27 + 9 +1 = 91 113 + 103 = 3x100 + 3x10 + 1 = 300 + 30 + 1 = 331 |
|
|
Deux nombres avec écart de 2 (n-1)3 +
(n+1)3 = n3 –
3n2 + 3n – 1 + n3 +
3n2 + 3n + 1 = 2n3 +
6n (n + 1)3
– (n – 1)3 = n3 +
3n2 + 3n + 1 – n3 +
3n2 – 3n + 1 = 6n² + 2 |
93 + 113 = 2x103 + 6x10
= 2 060 63 - 43 = 6x5² + 2
= 152 |
|
|
Trois nombres (n – 1)3
+ n3 + (n + 1)3 = n3 –
3n2 + 3n – 1 + n3 + n3 +
3n2 + 3n + 1 = 3n3 +
6n = 3n (n2
+ 2) |
93 + 103 + 113 = 30 (100 + 2)
= 3000 + 60 = 3060 |
|
|
Quatre nombres (centraux identiques) (n-1)3 + n3 +
n3 + (n+1)3 = n3 – 3n2 + 3n – 1 + n3 + n3 + n3 + 3n2 + 3n + 1 = 4n3 + 6n = 2n (2n2 + 3) |
53 + 63 +
63 + 73 =
12 (2 x 36 + 3) =
12 x 75
= 900 |
|
Voir Nombres
consécutifs / Calcul
des cubes
|
|
|
|
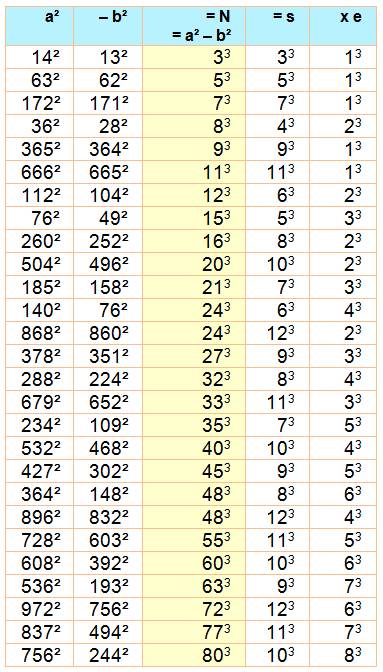
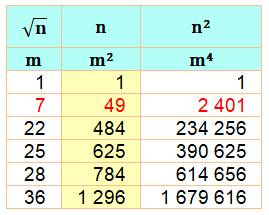
Recherche des cas tels que: Cube = différence de carrés = produit de deux cubes dont la somme et la différence
sont celles des nombres soustraits. Exemples de lecture de la table: 142 – 132 = 196 – 169 = 27 = 33 = 33 x 13 &
14 + 13 = 27 et 14 – 13 = 1 Table
pour a et b jusqu'à 1000 et n < 101
|
|
Voir Différence de carrés = produit
de carrés
|
|
|
|
·
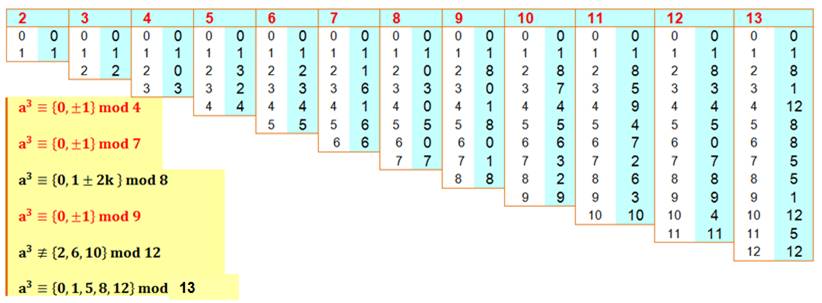
Quels sont les restes possibles de la division d'un
cube par un nombre de 2 à 13? ·
Dans le cas de la division par
2, si le nombre est pair (2k) le cube est pair; si le nombre est
impair (2k + 1), le cube est impair. Le cube conserve la parité. ·
Dans le cas de la division par
3, le reste est égal à {0, 1 ou 2} et le reste de la division par
3 du cube est {0, 1 ou 2}. Le cube
conserve le reste. On dit que: a3 = a mod 3. ·
Dans le cas de la division par
4, selon le reste {0, 1, 2 ou 3}, le reste de la division du cube par
4 donne seulement {0, 1, 3} que l'on peut écrire {-1, 0, +1} car -3 est
équivalent à 1 dans le monde des "modulos". On note a3 =
{0, Tableau: colonne bleue =
reste de la division par n (rouge) du cube pour un nombre donnant le reste
indiqué à gauche
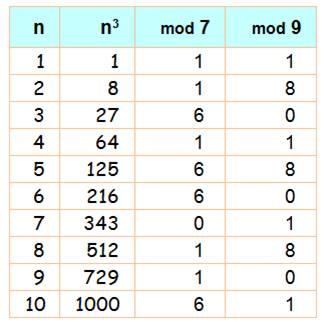
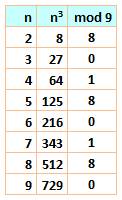
La division par 7 et par 9 des cubes est à noter: les
restes sont nuls ou plus ou moins 1. Autrement dit: Un cube est un
multiple de 7 ou un multiple de 7 plus ou moins 1. Un cube est un
multiple de 9 ou un multiple de 9 plus
ou moins 1. Voir Preuve par 9 Exemples
|
|
Suite Cubes
en modulo / Voir Divisibilité
|
|
||
|
· Ce qu'il faut démontrer Rappel: (A, B) = 1 est la forme abrégée de PGCD
(A, B). |
Si A . B =
C = c3 Et (A, B)
= 1 Alors A =
a3 et B = b3 |
|
|
· La factorisation première
d'un cube est telle que tous les exposants sont des multiples de 3 |
|
|
|
· Factorisation de A et B |
|
|
|
· A et B sont premiers entre eux.
Les facteurs premiers de A (qi) et ceux de B (ri) sont distincts. Chacun de manière
indépendante égale un facteur premier de C (pi). |
pi = {qi ou ri } |
|
|
· Ces égalités entre facteurs premiers entraînent celles sur les
exposants. |
bi = certains 3ai ci = les autres 3ai
|
|
|
· Dans A comme dans B les exposants sont des multiples de 3. |
A et B sont des cubes |
|
Voir Démonstration de Fermat pour n = 3
|
|
|||
|
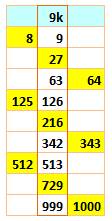
Un cube divisé par 9 donne un reste égal à 0 ou 1 ou 8. Les nombres cubes (jaune) sont tous multiples de 9 (9k) ou voisin d'un multiple de 9. |
|
On lit: un cube est égal à un multiple de 9 ou alors à un
multiple 9 plus 1 ou à un multiple de 9 moins 1. En maths on dit: un cube est égal à -1 ou 0 ou 1 modulo 9. |
|
|
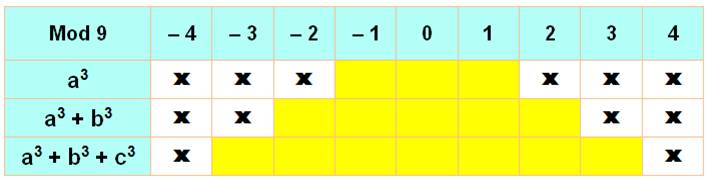
La somme de deux cubes n'est
jamais de la forme 9k Divisé par 9, le reste n'est jamais: 3, 4, 5 ou 6. |
|
||
|
La somme de trois cubes
n'est jamais de la forme 9k Divisé par 9, le reste n'est jamais:
4 ou 5 |
|
||
Voir Somme de cubes / Nombre 33 - Récalcitrant
|
Un
cube divisé par 9 donne un reste de 0, 1 ou 8 ou, en formule:
Cube
et somme de cubes mod 9:
Un
nombre en 9k + 4 ou 9k + 5 n'est jamais somme de trois cubes. |
Voir Explications / Modulo des cubes
Devinette avec somme de trois cubes
|
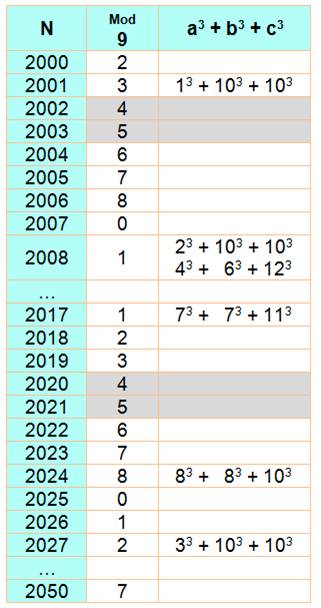
Question Quelle
sont les solutions de a3
+ b3 + c3 = 2 020 ? Solution 2
020 Avec
n3 Commentaires D'une
manière générale, aucune solution pour tout nombre congru à 4 ou 5 mod 9. Mais
aucune garantie de trouver une solution pour les autres nombres comme le
montre le tableau. De
2 000 à 2 050, il ya seulement 5 solutions dont une double pour 2 008. Il y
en a 9 dont une solution double pour l'autre moitié (2 050 à 2 100). |
|
|
|
||
|
Nombre
cube dont la somme des chiffres est la racine cubique du nombre. Hors le
trivial cas du 1, ils sont cinq. Henry Dudeney (1857-1930). |
|
|
|
Nombres généralisés de Dudeney avec
le carré |
81 = 9² |
|
|
Avec le bicarré |
|
|
|
Avec la puissance 5 |
17 210 368 = 285 52 521 875 = 355 60 466 176 = 365 205 962 976 = 465 |
|
|
Les plus grands pour les puissances
successives On a vu 81 pour le
carré, 19 683 pour le cube, etc. |
9, 81, 19683,
1679616, 205962976, 68719476736, 6722988818432, 248155780267521, 150094635296999121,
480682838924478847449, 23316389970546096340992, 2518170116818978404827136,
13695791164569918553628942336, 4219782742781494680756610809856, … |
|
Voir Suite en puissance de la somme des
chiffres / Nombre
512
Quantité de même chiffre dans un cube
|
Plus petit nombre au cube avec quatre chiffres k Exemple: 7153 = 365 525
875 avec quatre fois le chiffre"5".
|
Voir Cubes avec
records de 3 et autres puissances /
Cubes
avec chiffres répétés / Nombres apocalyptiques
|
Cube avec nombres ajoutés à leur retourné. Testé
jusqu'à 100 000 |
23
= 8 = 4 +
4 73 = 343 = 122 + 221 = 320 + 23 113 = 1 331 = 1 030 + 301 = 1 120 + 211 = 1 210 + 121 = 1 300 + 31 |
553 = 166 375 = 67 199 + 99 176 = 68 189 + 98 186 = 69 179 + 97 196 = 77 198 + 89 177 = 78 188 + 88 187 = 79 178 + 87 197 = 87 197 + 79 178 = 88 187 + 78 188 = 89 177 + 77 198 = 97 196 + 69 179 = 98 186 + 68 189 = 99 176 + 67 199 |
|
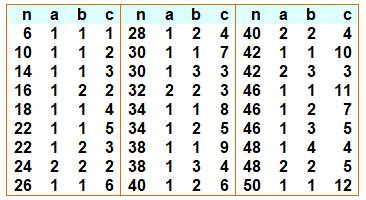
Ce sont des nombres pairs (> 4) qui ne sont
pas la surface d'un cube. Ils ne peuvent pas être de la forme: n = 2(ab +
bc + ca) Ils sont seize: 8, 12, 20, 36, 44, 60, 84, 116, 140, 156, 204,
260,
380, 420, 660,
and 924. Les solutions pour 6 à 50
|
![]()
![]()