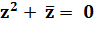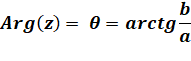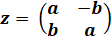Nombres complexes, portail

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/11/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de NOMBRES
Débutants Type de nombres	NOMBRES COMPLEXES			Glossaire Nombres
INDEX Type de Nombres	Aiguillage	Débutants	Introduction	Glossaire
		Cours de Terminale		RADICAL
		Sommaire de cette page >>> Index par rubrique >>> Vocabulaire du monde des complexes

NOMBRES COMPLEXES

Portail – Aiguillage – Index –

Table des matières – Orientation …

Vocabulaire, lexique, glossaire

NOMBRES COMPLEXES

– Index par rubriques principales

Général

Débutants	Introduction	Vocabulaire
Historique	Applications	Résumé – Glossaire

Cours de terminale – Résumé du cours

Cours de terminale – Technique opératoire

Cours de terminale – Exercices (bac)

Familles

Place (type)
Tableau de famille	Complexes	Quaternions
Trois algèbres	Cyclotomique (1)	Octavions
	Cyclotomique (2)

Forme

Cartésienne	Polaire	Exponentielle
Matrice

Cercle trigonométrique

Calcul de sommes trigonométriques

Calcul de 1 ± cos a + i sin a

Opérations

Opérations	Addition	Multiplication
Conjugué	Soustraction	Division
Racine quatrième

Formules

Identités de base	Factorisation	Puissances
Identités avec i

Formulaire

Euler

De Moivre

Puissance

Réelle (principes)	Réelle (calculs)	Imaginaire
Réelle entière		Complexe

Nombres entiers de la forme: (1 + i)ⁿ + (1 – i)ⁿ = 2^k

Racine

Racines nièmes	Racine de l'unité (1)	Racine de l'unité (2)
Racine de i et -i	Exemples de calculs	RADICAL

Logarithme

ln (a + i b)

Entiers

Entiers de Gauss	Entiers d'Eisenstein
Conjugués Entiers	Puissance réelle entière

Calculs

Conjugués	Factorisation	Puissances
Conjugués Entiers	Calculs avec i	Somme de carrés (1)
Calcul de somme	Dans le carré	Somme de carrés (2)

Calcul par méthode du componendo et dividendo

Résoudre l'équation

Module de z dans i z³ + z² – z + i = 0

Calcul de 1 ± cos a + i sin a

Calculs en trigonométrie

Géométrie

Colinéarité et orthogonalité

Hauteurs du triangle concourantes – Démo

Vocabulaire
i Imaginaire unité		Symbole représentant la racine carrée du nombre négatif (–1). Base des nombres complexes.	i Imaginary unit
j		Une des racines complexes de ou i chez les électroniciens.	j
a + i b	z = a + i b	Nombre complexe. Dit sous sa forme cartésienne algébrique.	Complex number
(a, b)	z = (a, b)	Représentation d'un nombre complexe par une paire ordonnée de nombres. Dit sous sa forme cartésienne vectorielle.	Ordered pair
Partie réelle	Re(z) = a	Nombre réel classique. Deux symboles possibles.	Real number
Nombre imaginaire	Im(z) =b (z)	Nombre précédé du symbole i. Deux symboles possibles.	Imaginary number
Nombre imaginaire pur Nombre totalement imaginaire	z = i b	Nombre complexe dont la partie réelle est nulle	Purely imaginary
Nombre complexe	z	Nombre du type a + i b	Complex number
Corps des nombres complexes		Ensemble des nombres complexes avec a et b deux nombres réels.	Complex field
Plan complexe (de Gauss)		Système de coordonnées cartésien avec la partie réelle en abscisse et la partie imaginaire en ordonnée. >>>	Complex plane Gaussian plane Argand plane
Point image	M (a + i b)	Point image du nombre complexe.	Image
Image vectorielle		Vecteur qui part de l'origine des axes et atteint le point M.	Vector image
Affixe	a + i b	Nombre complexe caractérisant le point M. Aussi: coordonnées complexes du point M.	Affix
Conjugué	= a – i b	Nombre complexe dont la partie imaginaire est opposée. Utile pour la division. Parfois aussi noté z*.	Conjugate
Module Se lit: z barre		Longueur du segment OM dans le plan complexe. Norme du vecteur OM.	Modulus
Argument ou phase		Angle xoM dans le plan complexe. Non défini si a = 0 et b = 0. Angle défini à près.	Argument or phase
Forme cartésienne	z = a + i.b	Point dans le plan complexe cartésien	Rectangular form
Forme trigonométrique Coordonnées polaires		Le couple module et argument suffit pour désigner un point M.	Polar coordinates Polar form
Coordonnées polaires Forme exponentielle		Expression découlant de la formule d'Euler:	Exponential form
Forme matricielle		Matrice de similitude directe. Module = rapport de la similitude. Argument = angle de la similitude.	Matrix form
Nombre zéro	0	Il est à la fois réel et imaginaire. Seul nombre complexe dont le module est nul.	Zero number
Image Se lit M prime; sans rapport avec la dérivée	M' image de M par l'application F	Une application complexe f (z). Un point M (a+ ib) Le point image M' (a'+ib' = f(a+ib) )	Image under the transformation