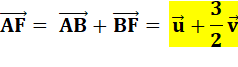Avec exemple résolu in fine >>>

 

 

 

 

Approche

 

*    Des lignes, des segments ou des vecteurs sont colinéaires s'ils sont tous sur la même ligne, ou se dirigent tous dans la même direction; s'ils sont parallèles, en fait.

 

*    Des points sont alignés s'ils sont portés par la même droite.

 

 

 

*    Des lignes, des segments ou des vecteurs sont coplanaires s'ils sont dessinés sur un plan ou sur des plans parallèles; ils sont tous horizontaux ou verticaux ou obliques de la même manière.

 

 

D1, D2, D3 sont colinéaires

 

 

D1, D2, D3 sont coplanaires

 

Voir Mots croisés

 

 

Colinéaires

 

*       Deux droites définies par les équations sont colinéaires si elles ont même coefficient directeur.

 

Illustration

Ces droites parallèles (ou colinéaires) ont le même coefficient directeur. Leur équation y = ax + b présente la même valeur de a (1/2) pour des valeurs de b, ordonnée à l'origine, différentes

 

 

 

 

*    Deux vecteurs du plan, ou de l'espace sont colinéaires
si, et seulement si:

*    ils ont même direction (par forcément même sens) ou bien si l'un d'entre eux est nul.

*    ou (autre définition)

*    l'un d'entre eux est le produit de l'autre par un réel.
            .

  Voir Exemple de démonstration

 

*    Si ,  et  sont colinéaires si, et seulement si, il existe un réel tel que  .

 

*    Deux vecteurs non-colinéaires sont dits indépendants.

 

*    Trois points A, B et C sont alignés si, et seulement si, les vecteurs  et   sont colinéaires (ils appartiennent à la même droite.

 

Suite en Vecteurs – condition de colinéarité

 

 

Coplanaires

 

*    Trois vecteurs de l'espace sont coplanaires
si et seulement si:

*    leurs directions sont parallèles à un même plan ou bien si l'un d'entre eux est le vecteur nul.

*    ou (autre définition)

*    l'un d'entre eux est la combinaison linéaire des deux autres.
          .

 

*    Si  et  ne sont pas colinéaires, ,  et   sont coplanaires si, et seulement si, il existe deux réels tel que  .

 

*    Trois vecteurs non-coplanaires sont dits indépendants.

 

*    Quatre points A, B, C et D sont coplanaires si, et seulement si, les vecteurs  ,   et  sont coplanaires (ils appartiennent au même plan).

 

 

 

 

Remarqué

 

Quantité d'objets

Vecteurs

Points

Colinéaires

2 dans l'espace

3 sur une droite

=> Alignés

Coplanaires

3 dans l'espace

4 dans un plan

=> Coplanaires

 

 

 

 

Alignement de points – Démonstration

 

Idée générale de l'énoncé

 

Un parallélogramme.

Sur les côtés, des vecteurs de longueur 1/3 et 3/2.

Démontrer un alignement.

 

 

Mes déclics …

 

Le parallélogramme  => la somme de vecteurs.

Alignement => vecteur proportionnel: 

Rapport k => sans doute dans la relation entre 1/3 et 3/2?

 

Le problème pas à pas

Trois points A, B et C non alignés.

Tracé des vecteurs u et v sur AB et AD.

 

Pour tracer w, somme de u et v, je translate un vecteur équipollent à v pour amener son origine au point B. Son extrémité est le point C. Et, le vecteur AC est le vecteur w cherché.

 

Tracé du quadrilatère  ABCD. Ce quadrilatère est un parallélogramme.

 

 

Dans le parallélogramme ABCD:

Tracé des vecteurs s et t  avec les relations vectorielles indiquées sur la figure.

 

J'observe que les points A, E et F sont alignés. Hasard?

 

Déclic:
Triangles ABF et ECF
=> Thales => proportionnalité
=> Bien sûr: A, E et F alignés.

Après avoir déplacé D en D', je reprends toute la construction et constate à nouveau l'alignement des points A, E et F.

Démontrons cette propriété.

 

Démonstration de la colinéarité

 

Relation de Chasles

Toujours avec cette relation, en passant par des vecteurs connus.

En reprenant:

Quant à AF:

Un petit air de réciprocité entre les deux vecteurs … Et si on multipliait l'un par k = 2/3.

Conséquence:

L'un des vecteurs est le produit de l'autre par un réel k, ils sont colinéaires.

A est un point commun, les points A, E et F sont alignés.

Merci Kristin

Compléments

 

Propriété vraie pour les rapports 1/3 et 3/2. Et, si nous cherchions d'autres rapports qui marchent.

Proportionnel:

u + bv = K(1 – a) u + Kv

Conclusion pour b:

b  = K

Conclusion pour a:

1  = K(1 – a) = b(1 – a)

Exemple avec b = 3/2.

On aurait donc pu choisir bien d'autres valeurs pour a et b:

 

Prenons le parallélogramme particulier qu'est le rectangle pour nous rendre compte de cette propriété.

 

Ici, le théorème de Thalès, montre bien les proportionnalités dans les triangles rectangles.

 

Observez les limites
Pour b  = 1 et a = 0 (les points E et F sont confondus en C).
Quand b tend vers l'infini (le point F "au bout" de la verticale), alors a  = 1 (le point E se trouve en D).

 

 

 

 

Suite

*         Vecteurs

*         Droite

Voir

*           Géométrie – Index

*           Enseignement – Index

Cette page

http://villemin.gerard.free.fr/Referenc/Vocabula/GlosC/Colineai.htm