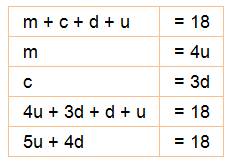|
||||||||||||||||||||||||||||||||||||||||
Voir Décimal et toutes ses
significations
![]()
Système décimal vu par Laplace (1749-1827)
|
Le système
décimal de position: C'est
de l'Inde
qui nous nous vient l'ingénieuse méthode d'exprimer tous les nombres avec dix
caractères, en leur donnant à la fois une valeur absolue et une valeur de
position. Idée
fine et importante, qui nous paraît maintenant si simple que nous en sentons à peine le mérite. Mais
cette simplicité même et l'extrême facilité qui en résulte pour tous les calculs
placent notre système d'Arithmétique
au premier rang des inventions
utiles. Et,
l'on appréciera la difficulté d'y parvenir si l'on considère qu'il a échappé
au génie d'Archimède
et d'Apollonius,
eux des plus grands hommes dont l'Antiquité s'honore. |
Œuvres complètes de Laplace Livre V –
Chapitre I – Exposition du système du monde
|
Système décimal
|
|
Quelle
est la somme de tous les chiffres pour écrire tous les nombres inférieurs à
1000? |
|
APPROCHE |
|
|
Exemple avec mes boites de rangement de la monnaie
Les
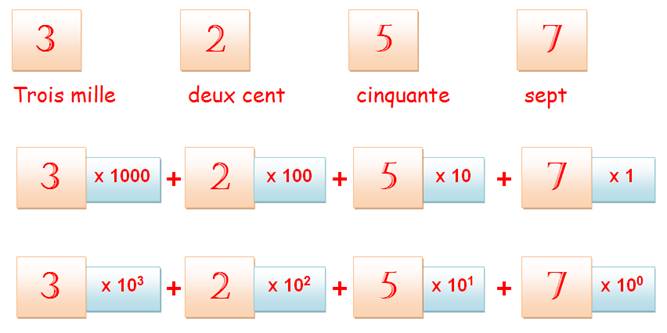
billets sont factices 3 x 100 + 2 x 10 + 4 x 1 = 324 euros Voir Chiffres / Décomposition |
|
|
|
|
|
Et la représentation générique: 3257 = 3 x 103 + 2 x 102 + 5
x 10 + 7 N = a3 . 103
+ a2 . 102 + a1 . 10 + a0 N = … + ai . 10i
+ …+ a3 . 103 +
a2 . 102 + a1 . 10 + a0 |
|
Voir Puissances / Puissances de dix / Multiplications pyramides / Simplification singulière de
fractions
|
|
|
|
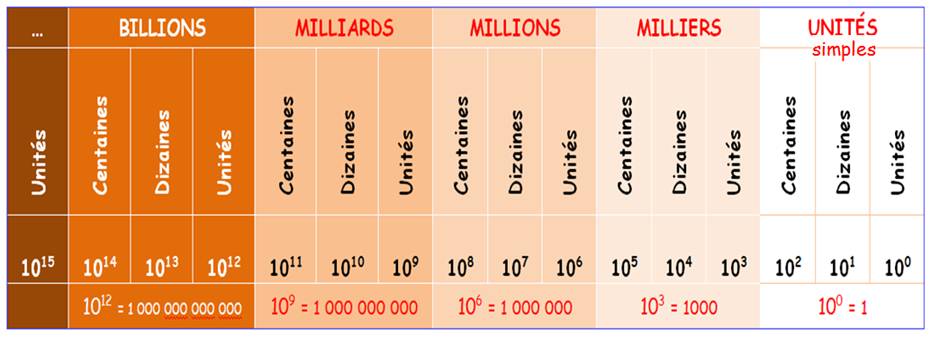
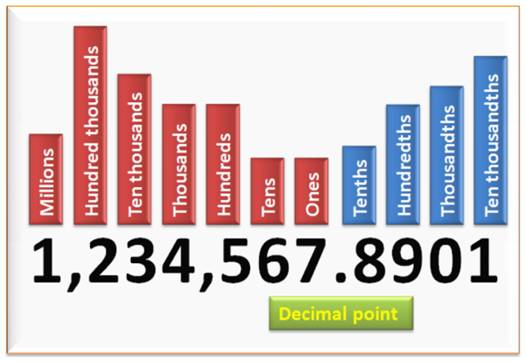
Six-cent-cinquante-sept-BILLIONS huit-cent-quatre-vingt-dix-MILLIARDS cent-vingt-trois-MILLIONS quatre-cent-cinquante-six-MILLE sept-cent-quatre-vingt-neuf.
|
|
Voir Écriture par tranche de 3 chiffres / Billions, Trillions … / Orthographe
des nombres / Les
nombres en toutes lettres
Calcul de la quantité de chiffres
/ Extraction des chiffres dans un
nombre
|
|
|||
|
Voir Multiplications et divisions par
10 - Exemples
Ainsi un milliardième s'écrit (même quantité de
zéros de chaque côté du signe égal):
Quantité de zéros
Multiplication et division par 10
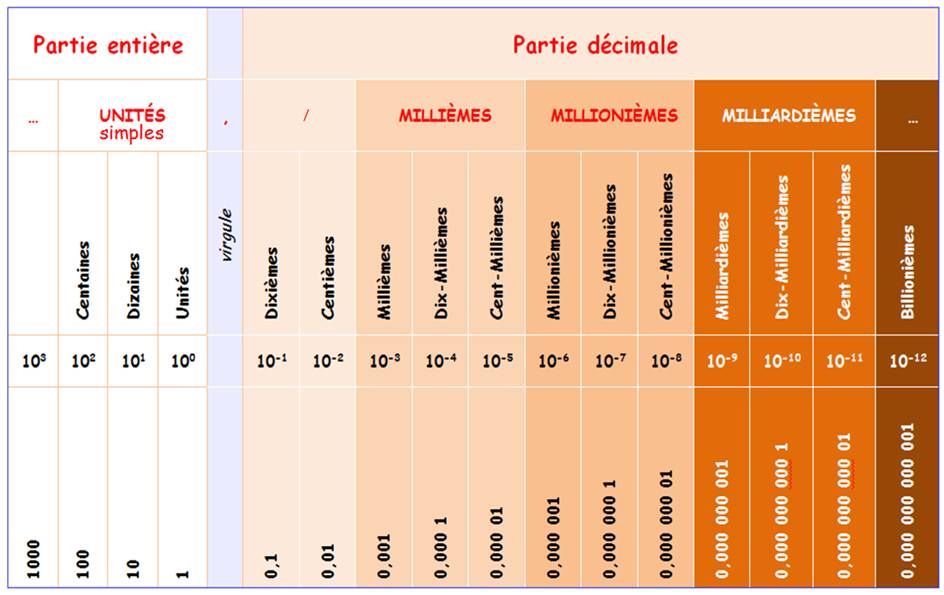
Zéro virgule cent-vingt-trois, quatre-cent-cinquante-six,
sept-cent-quatre-vingt-neuf.
Zéro virgule cent-vingt-trois millièmes, quatre-cent-cinquante-six
millionièmes, sept-cent-quatre-vingt-neuf milliardièmes.
Zéro virgule un dixième deux centièmes, trois millièmes, quatre
dix-millièmes, cinq cent millièmes, six millionièmes, sept dix millionièmes,
huit cent millionièmes, et neuf milliardièmes.
N =
… + ai . 10i + …+ a3 . 103 + a2
. 102 + a1 . 10 + a0 , a-1 . 10-1 + , a-2
. 10-2 + … , a-j . 10-j + … |
|||
Voir Nombres décimaux / Nombres
périodiques / Mantisse
|
Unités simples et dixièmes/centièmes … Extrait
du cours
de mathématiques de Charles Bossut. Notez qu'en 1800, la notion d'unités
simples existait déjà.
Notation avec la virgule comme séparateur décimal 1595 – Bartholomäus Pitiscus, astronome, mathématicien
et théologien allemand aurait utilisé (occasionnellement) la virgule dans ses
tables de trigonométrie. Simon Stevin (1548-1620) aurait transformé la notation
fractionnaire Exemple: 12,345 s'écrivait 12 3/10 4/100 5/1000 ou aussi 12
345/1000. Il écrit 12(0) 3(1) 4(2) 5(3). 1615 – John
Neper (1550-1617) dans ses tables de logarithmes, il remplace le 0 par
une virgule et laisse tomber les autres exposants: 12,345. Note: la Conférence générale des poids
et mesures autorise aussi l'utilisation du point dit point
britannique: cas notamment des États-Unis, de l'Australie, du
Royaume-Uni et de la Suisse. |
|
La
somme de mes chiffres est 18. Mon chiffre des milliers est quadruple de celui
des unités et mon chiffre des centaines est le triple de celui des dizaines.
Qui suis-je? Petits travaux avec des égalités
Raisonnement pour trouver la solution Les
valeurs de u et d sont proches car leurs poids (5 et 4) sont voisins. S'ils
étaient égaux, nous aurions: 9d = 18 et d = 2. Essayons
u = d = 2, alors: 5 x 2 + 4 x 2 = 18. Ça marche! Le
nombre cherché est: 8622. Solution unique. Un autre nombre … Somme
des chiffres: 18, milliers cinq fois les unités et centaines deux fois les
dizaines. Seule solution: 5841. |
Voir Jeux
et énigmes
|
|
|
|
Place value chart Decimals
are a way to represent fractions. Decimals and fractions both represent
values in-between two whole numbers. Between
the numbers 2 and 3 there are billions and billions of other numbers. In
fact, the actual amount of numbers between 2 and 3 is endless. Why
do decimals start with the "tenths" place instead of the
"oneths" place? The reason is because 1/1 is the same as 1, which
is in the ones place. |
|
|
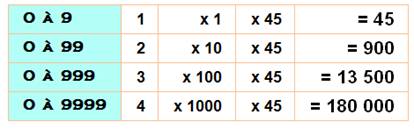
Quelle
est la somme de tous les chiffres pour écrire tous les nombres inférieurs à
1000 ? Solution Les
nombres s'écrivent: 000, 001, … 100, 101, …998, 999. chacun
des chiffres apparait 100 fois en position unité, 100 fois en position
dizaines et 100 fois en position centaines. La
somme: S = 3 x 100 x (1 + 2 + … + 9) = 300 x 9 x 10 / 2 = 300 x 45 =
13 500 Somme selon la quantité de
nombres
|
![]()
|
Suite |
|
|
DicoNombre |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()