Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 02/12/2024 M'écrire Brèves de Maths

Orientation Glossaire	Atlas / Géométrie / Transformation
Débutant DicoMot DicoNombre	SYMÉTRIE Jeune Guépard

Amusement

Les visages ne sont jamais parfaitement symétriques.

Au centre le vrai portrait. De chaque côté, les symétriques exacts de chaque moitié de visage.

Source image: Facial anatomy and proportions

Approche	Un tache d'encre ou de peinture; je plie la feuille en deux et j'obtiens une image jumelle, un clone, une image symétrique par rapport à l'axe de pliure. Une image sur une feuille; je punaise un coin et fait pivoter d'un demi-tour; j'obtiens une image tête en bas; en fait une symétrie par rapport au point où j'ai placé la punaise.
En 3D	Si vos deux mains étaient absolument semblables, l'une serait l'image de l'autre dans un miroir. Pourtant elles ne sont pas superposables. On dit qu'elles sont énantiomorphes. Pour passer de l'une à l'autre, il faudrait les retourner comme un gant, impossible sinon en 4D!
Définition	Symétrie AXIALE ou symétrie ORTHOGONALE: La symétrie orthogonale dans le plan et d'axe la droite D, appelée aussi réflexion d'axe D, est l'application du plan qui à tout point M associe un point M' tel que D soit la médiatrice du segment [MM']; si M est un élément de D, alors M = M'. Symétrie CENTRALE: La symétrie centrale dans le plan et de centre O est l'application du plan qui à tout point M associe un point M' tel que O soit le milieu du segment [MM'].

Voir Symétries - Débutant / Jeux de symétrie

Famille

La symétrie est une application affine bijective. Application Bijection Transformation Isométrie Symétrie Les symétries axiales et centrales sont des involutions (la symétrie appliquée deux fois de suite redonne l'image d'origine). La symétrie centrale est un déplacement (angles orientés conservés). La symétrie axiale est un antidéplacement (angles orientés sont opposés). La symétrie centrale est équivalente à une rotation de centre O et d'un angle égal à (demi-tour).

Invariants

La symétrie axiale ou centrale est bijective Conservation des longueurs les segments symétriques ont même longueur; Conservation des angles les angles symétriques ont même ouverture; Conservation des aires les figures symétriques ont même aire.

Propriétés	Toute isométrie du plan qui admet exactement une droite de points invariants est une symétrie axiale. Toute isométrie du plan peut être décomposée en le produit d'au plus trois symétries axiales distinctes.
Composées	Composée de deux symétries centrales: la composée de la symétrie de centre A et de la symétrie de centre B est la translation de vecteur . Composée de deux symétries axiales: la composée de deux symétries axiales par rapport aux droites D et D' est un déplacement soit une translation si D est parallèle à D'; soit une rotation de centre O si D et D' sont sécantes en O.
"Théorème fondamental"	Propriété découverte par Évariste Galois Tout comme les molécules sont composées d'atomes ou comme les nombres peuvent être décomposés en nombres premiers, les objets symétriques peuvent être décomposés en objets symétriques indivisibles. Par exemple pour un polygone régulier de quinze côtés, ses symétries peuvent être construites à partir d'un pentagone et d'un triangle équilatéral. Pour obtenir la rotation de 1/15 de tour, il faut tourner le pentagone de 2/5 et le triangle de 1/3 de tour dans l'autre sens. En effet : 2/5 – 1/3 = 1/15. Bilan : les symétries d'un n-gones régulier sont toujours décomposées avec les symétries de p-gones où p est premier.

Symétrie en physique

En physique les symétries caractérisent les répercussions sur l'espace et le temps des forces exercées par les particules. La symétrie T: renversement du temps, La symétrie P: parité La symétrie C: conjugaison de charge Selon le Modèle Standard de la physique des particules, la nature conserve la symétrie CPT. Les lois ne changent pas lorsque toutes les particules d'une interaction sont remplacées par leur antiparticule (C), les trois directions de l'espace sont inversées (P), et le temps est inversé (T). La nature viole la symétrie CP (charge-parité), mais il n'y a pas de preuve expérimentale de violation de la symétrie CPT.

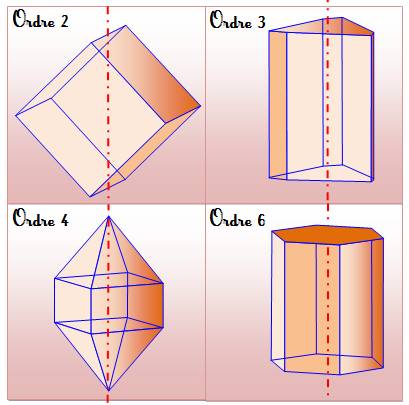
Symétrie en cristallographie

La cristallographie est le monde de la symétrie. Sept systèmes cristallins sont définis selon les axes de symétries des mailles des cristaux. L'ordre 3, par exemple, signifie que l'on retrouve la même forme après une rotation de 360° / 3 ou que trois telles rotations ramène l'objet dans sa position initiale. Un axe de symétrie passe par des points opposés qui peuvent être les sommets, les milieux des arêtes ou encore le centre des faces.

Vocabulaire : AXE et CENTRE de SYMÉTRIE

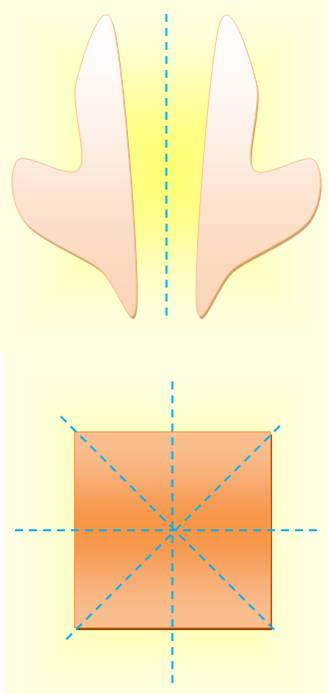
Axe de symétrie

Une droite est un axe de symétrie d'une figure si, après pliage le long de cette droite, les deux moitiés de la figure se superposent. La figure ci-contre présente un axe de symétrie (pointillé bleu). Les quatre axes de symétrie du carré.

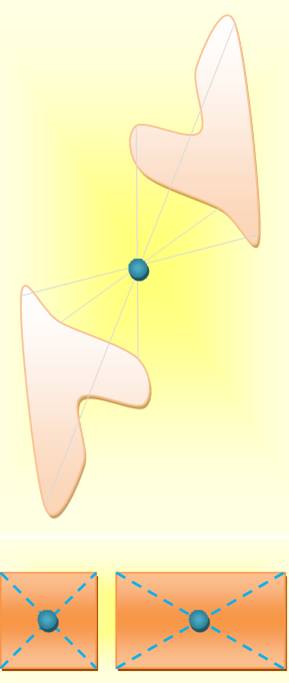
Centre de symétrie

Une figure a un centre de symétrie si, lorsqu'on la fait tourner d'un demi-tour autour de ce point, elle ne varie pas. La figure ci-contre présente un centre de symétrie (point marron). Le centre du carré est un centre de symétrie. C'est aussi le cas du point d'intersection des diagonales du rectangle.

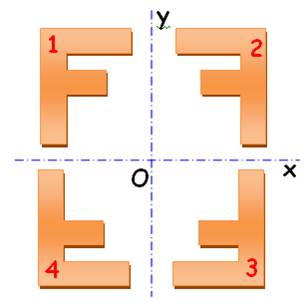
Symétrie et Rotation	On prend souvent la lettre F pour visualiser les transformations. Que devient la lettre F vue à travers des miroirs positionnés sur y et sur x?
	1 2 Symétrie d'axe y 2 3 Symétrie d'axe x 3 4 Symétrie d'axe y 4 1 Symétrie d'axe x		1 3 Symétrie de centre O, ou Rotation 180° de centre O.
	Note: dans un miroir vous vous voyez à l'envers (comme F2) Avec deux miroirs à 90°: vous vous voyez tel que vous êtes, comme tous les autres vous voient.

L'ATLAS

Le recensement de toutes les symétries a été publié en 1985 sous le nom de Altlas of finite groups, souvent désigné simplement par l'Atlas. Ses auteurs (notez qu'ils s'écrivent tous avec six lettres): John Horton Conway, Robert Turner Curtis, Simon Phillips Norton, Richard Alan Parker, et Robert Arnott Wilson Ce document détaille les 93 groupes finis simples et autres (total 716) qui on été identifiés, principalement sous l'impulsion de Conway. Sa forme électronique se trouve en ATLAS of Finite Group Representations It currently contains information (including 5215 representations) on about 716 groups.

Notions avancées: groupes de symétries**

SO SU

Groupes de symétrie: groupe de toutes les isométries laissant un objet invariant. Felix Klein: la géométrie devrait être comprise comme l'étude des invariants sous un groupe de transformations donné (programme d'Erlangen- 1872). La théorie de ces groupes est particulièrement importante pour traiter la physique moderne: électromagnétisme, relativité, physique quantique. Le modèle standard de la physique des particules a été presque entièrement construit grâce aux concepts de symétrie et d’invariance. On distingue: SO(n): groupes spéciaux orthogonaux, préservant le produit scalaire d’un espace vectoriel réel euclidien de dimension finie n. SO(2) ou U(1): groupe de rotation du cercle. SO(3): groupe de rotation en 3D, comme pour la sphère. SU(n): les groupes spéciaux unitaires, préservant le produit scalaire d’un espace vectoriel complexe hermitien de dimension finie n. SU(2), par exemple est le groupe de jauge de la force nucléaire faible. SU(3), par exemple est le groupe de jauge de la force nucléaire forte. Il décrit par exemple les trois couleurs des quarks. Su(3,1), groupe de Lorentz, préservant une forme quadratique de signature d’un espace vectoriel réel de dimension 4. Il particulièrement important en relativité (facteur de Lorentz). Il est le groupe naturel de symétries vectorielles de l'espace-temps R^3,1. U(1) x SU(2) x SU(3) est le groupe de jauge du modèle standard. Groupes de Lie: un concept de symétrie continue reliant géométrie et algèbre (idée de déplacements très petits comma la rotation du cercle ou de la sphère; utilisation du calcul différentiel). On s'intéresse aux propriétés de symétrie des espaces finis. Les groupes de transformations de ces espaces, comme les rotations, préservant ces structures, portent le nom de groupes de Lie. Sophus Lie (1842-1899) a eu l'idée de s'intéresser aux symétries sous-jacentes des équations pour les résoudre plus simplement.

Anglais	Symmetrical about a line: a plane figure is symmetrical about a line L if, whenever P is a point of the figure, so too is P', where P' is the mirror-image of P in the line L. The line L is called a line of symmetry. The figure is said to have bilateral symmetry. Symmetrical about a point: a plane figure is symmetrical about a point O if, whenever P is a point of the figure, so too is P', where O is the midpoint of PP'. The point O is called a centre of symmetry. The figure is said to have half-turn symmetry about O.
En savoir plus	Voir suite en cliquant sur les mots de l'en-tête 38 en miroir Billard et symétrie Chiffres en miroir Chiral Éléments de géométrie Frises, papier peint, cristaux Géométrie – Index Groupe de symétrie S3 Groupes de symétrie Palindromes Programme de Langlands Symétrie Symétrie – Débutant Symétrie et isométrie des triangles Symétrie des polyèdres Tits Jacques – Expert et théorie des groupes Triangle et symétrie: notion de groupe
Sites	Transformations – Wikipédia Groupe de symétrie – Wikipédia Jouons avec la symétrie – Introduction à la cristallographie The symetry of crystals (voir chapitre 3) – Nombreux exemples en images et animations Introduction aux groupes de Lie pour la physique – Fréderic Paulin – 2017 – pdf 125 pages
Livre	La symétrie ou les maths au clair de lune – Marcus du Sautoy – Ed. Héloïse d'Ormesson – 2012 – 520 pages – 26 € – Abordable par tous.
Cette page	http://villemin.gerard.free.fr/Referenc/Vocabula/GlosS/Symetrie.htm