Dictionnaire de base du vocabulaire des mathématiques P

p-adique* façon de représenter (développer) un nombre par des fractions de même dénominateur avec des puissances croissantes. Le p indique un nombre premier.
– v. Nombres p-adiques, dyadique, décadique, théorie des représentations
– a. p-adic number

Un nombre p-adique indique la fréquence avec laquelle apparaissent les puissances de p dans le nombre. Exemple pour 11 = 1 × 3² + 0 × 3¹ + 2 × 3⁰. Sa version 3-adique est 102.
Dans le monde des p-adiques, deux nombres considérés proches, non du fait d'une petite différence, mais si la différence est divisible plusieurs fois par p.
À chaque nombre premier correspond un système p-adique unique.
Ce sont des nombres plus faciles à étudier que les nombres rationnels. Chaque nombre p-adique est basé sur un premier unique, alors que les rationnels font appels à une infinité de nombres premiers sans structure apparente. Une propriété trouvée plus facilement dans le monde p-adique peut alors être projetée dans le monde des rationnels.
Par exemple, les 3-adiques sont propices à l'étude du polynôme x² = 3y² où le nombre 3 figure.
Les nombres p-adiques sont une petite fenêtre sur les nombre réels – Tasho Kaletha, University of Michigan.

p-premier: un nombre rationnel est p-premier si son dénominateur est premier avec p.
– a. p-prime

Pair (nombre -): nombre de la forme 2k; nombre divisible par 2.
– propriété: la somme des nombres pairs successifs est un rectangle dont la longueur et la largeur ne différent que d'une unité: 2 + 4 + 6 + … + 2n = n (n+1).
– v. Pair et impair
– a. Even (qui veut aussi dire: régulier, uniforme, plat).

Paire: ensemble constitué de deux éléments.
Généralement et notamment en théorie des graphes, une paire n'est pas ordonnée: (a, b) est identique à (b, a), sinon c'est un couple.
– syn. Couple, doublet, bipoint, 2-tuple, doubleton
– v. Singleton

Paire (fonction -): telle que f(-x) = f(x). Alors f(x) – f(-x) = 0
Le graphe d'une fonction paire est symétrique par rapport à l'axe des ordonnées.
– ex. x², cos (x).
– a. Even function

Palindrome: nombre qui se lit aussi de droite à gauche (1234321).
– v. Palindrome
– a. Palindrome

Palintiple**: nombre qui est multiple de son retourné.
– v. Palintiple

Pandigital: mot franglais, synonyme de pannumérique.

Pannumérique: qui utilise les neuf chiffres avec parfois le zéro en plus (123456789).
– v. Pannumérique
– a. Pandigitla

Papillon (effet -): cette théorie ne dit pas: petites causes, grands effets! Mais, petites variations dans les données de départ entraînent des comportements imprédictibles.
Plus positivement: cette théorie affirme que, même si des événements sont divergents, au final et statistiquement, ils s'accumulent sur un noyau de trajectoires nommé attracteur.
– origine: En 1972, Edward Lorenz donne une conférence dont le titre était : le battement d'ailes d'un papillon au Brésil peut-il provoquer une tornade au Texas ?
– v. Théorie du chaos, attracteur
– a. Butterfly effect: sensitive dependence on initial conditions, chaos theory

Paquet: bloc de données lors d'un transfert entre ordinateurs (surtout via Internet).
Le paquet est l'entité de transmission de la couche réseau (couche 3 du modèle OSI).
– a. Network packet: a formatted unit of data carried by a packet-switched network

Parabole: courbe comme celle dessinée dans une vasque.
Ou mieux, dessinée sur une antenne satellite parabolique.
Courbe plane dont chaque point est équidistant d'un point fixe appelé foyer et d'une droite fixe appelée directrice.
– Équation: y = ax² + bx + c
– v. Parabole, conique, quadratique
– a. Parabol

Paraboloïde: surface ou volume engendré par une parabole en rotation sur son axe principal.
– v. Paraboloïde
– a. Paraboliod

Paraboloïde hyperbolique: surface en forme de selle de cheval
– ex. illustration avec le point-col (flèche rouge)
– a. Hyperbolic paraboliod

Paradoxe ou proposition paradoxale: proposition qui semble vraie et fausse à la fois.
– v. Paradoxe
– a. Paradox

Parallèle: caractérise deux courbes qui ne rencontrent jamais, comme les rails de chemin de fer.
– étym. Du grec: para auprès et allelon l'un l'autre.
– v. Parallèle, types de lignes, concourantes, perpendiculaire, axiome d'Euclide, théorème des milieux
– a. Parallel line

Parallèle (segments, vecteurs -): segments ou vecteurs portés par des droites parallèles.
– a. Parallel segment, parallel vector

Parallèle géographique: cercle dessiné sur la Terre "parallèle" à l'équateur; intersection imaginaire du globe terrestre avec un plan parallèle au plan de l'équateur.
– v. Sphère terrestre, latitude

Parallélépipède ou pavé: polyèdre à six faces (parallélogrammes), parallèles deux à deux.
Il est droit si quatre faces sont des rectangles.
Il est dit rectangle si les six faces sont des rectangles.
Le parallélépipède rectangle ou pavé droit a la forme d'une boîte à chaussure ou d'une brique.
Son volume est égal au produit longueur x largeur x hauteur.
– étym. Du grec: para auprès, allelon l'un l'autre et epipedon surface unie.
– v. Parallélépipède, rhomboèdre
– a. Parallelepiped

Parallélogramme: quadrilatère dont les côtes sont parallèles deux à deux.
Les côtés opposés ont même longueur.
Les diagonales se coupent au point milieu de chacune.
Rectangles et losanges sont des parallélogrammes particuliers
– v. Parallélogramme
– a. Parallelogram: quadrilateral with two pairs of parallel sides, rhomboid

Parallélotope**: polytope, généralisation du parallélogramme et du parallélépipède aux dimensions supérieures.

Paramètre: nombre qui peut varier à volonté; faire varier un paramètre pour apprécier la sensibilité du résultat selon ce paramètre;
– notation: m ; ex: f_m(x) = ax² + mx + 1
– v. Coefficient, variable
– a. Parameter

Paramètres de tendance: regroupe moyenne, médiane, mode et quartiles.
– v. Vocabulaire des statistiques

Paramètres de dispersion: regroupe étendue, écart-moyen, écart-type et variance.
– v. Statistiques

Paramétrée (courbe -): les valeurs des coordonnées sont exprimées en fonction d'une variable tierce dite paramètre.
– ex. x = t² – 4 et y = 5t.

Paramétrique (représentation -): les équations d'une fonction comportent alors une variable auxiliaire souvent désignée par t.
– exemple générique: x = f(t) et y = g(t).
– exemple du cercle: x = a + r cos θ et y = ab + r sin θ.
– a. Parametric equation

Parenthèses: elles servent à bien identifier (isoler) un calcul qui doit être effectué avant d'autres.
Les termes insérés dans la parenthèse doivent être considérées comme un paquet.
Lorsque c'est possible, les termes dans la parenthèse seront calculés en premier.
– ex. 3 (10 – 4) = "trois fois le paquet (dix moins quatre)" = 3 x 6 = 18.
a (c – d) – b (c – d) = "a fois le paquet ( c – d) moins b fois le paquet (c – d)", soit (a – b) fois le paquet (c – d) = (a – b) (c – d).
On peut aussi distribuer le paquet:
– ex. a (c – d) – b (c – d) = [ac – ad] – [bc - bd] = ac – ad – bc + bd.
– v. Parenthèses
– a. Parenthesis

Parenthèses bien équilibrées: paires de parenthèses telles que chaque parenthèse ouvrante et accompagnée d'une parenthèse fermante.
– ex. pour n = 3, il ya cinq possibilités: ( ( ( ) ) ), ( ( ) ) ( ) , ( ( ) ( ) ) , ( ) ( ( ) ), ( ) ( ) ( ).
La quantité de possibilités pour n paires et le nombre de Catalan d'ordre n.
– v. Parenthèses bine équilibrées
– a. Balanced parenthesis

Parfait: se dit d'un nombre entier naturel dont la somme des diviseurs stricts est égale au nombre lui-même.
– ex. la somme des diviseurs stricts de 6 (1, 2, 3) est 6. Le nombre 6 est parfait.
Plus petit, le nombre est déficient; plus grand, il est abondant.
– a. Perfect number

Parité: 5 est un nombre de parité impaire alors que 4 est de parité paire.
Selon le reste de la division par 2 (0 ou 1), le nombre est pair ou impair.
– v. Pair/Impair
– a. Parity

Parité d'une fonction: paire si f(-x) = f(x); impaire si f(-x) = - f(x).
– a. Parity of even and odd functions

Fonction de parité: fonction booléenne qui prend la valeur vrai si et seulement si les arguments qui prennent la valeur vrai sont en nombre pair.
– a. Parity function

Partie: portion, morceau d'un tout.
– a. Part, portion, share

Partie d'un ensemble: synonyme de sous-ensemble.
Un ensemble de n éléments comporte 2ⁿparties.
– a. Subset, part of as set

Partie propre d'un ensemble: un sous-semble non vide et non plein.
– ex. E = {a, b, c} alors: {a,b} ou {a,c} ou {b,c} sont des parties propres; { } et {a,b,c} ne le sont pas.
– a. proper part of a set: non-empty part of a set E, that is different from E.

Partie entière, partie décimale ou fractionnaire: dans 12,34, le nombre 12 est la partie entière, alors que 34 est la partie décimale ou fractionnaire.
– notation: E(12,34) = 12;
– attention aux nombres négatifs ! E(– 2,3) = – 3
– v. Arrondis, plancher, plafond
– a. Floor and ceiling functions

Partie réelle et partie imaginaire: premier et deuxième terme d'un nombre complexe.
– a. Real part, imaginary part, imaginary unit

Partie aliquote: synonyme de diviseur propre.
Partie aliquante: non diviseur propre comme, par exemple, 5 pour 14.
– a. aliquot and aliquante parts

Partition d'un ensemble* découpage de l'ensemble complet en sous-ensembles.
Ceux-ci sont disjoints, non vides et, réunis, ils reforment l'ensemble complet.
– a. Partition of a set

Partition d'un nombre: toute somme donnant ce nombre.
Chaque terme est appelé sommant.
– ex. les sept partitions de 5 sont 1+1+1+1+1 = 1+1+1+2 = 1+2 +2 = 1+1+3 = 2+3 = 1+4 = 5.
– v. Partition
– a. Partition

Pascal (Pa): unité de pression du SI.
C’est la pression ou la contrainte uniforme qui, agissant sur une surface plane de 1 m², exerce perpendiculairement à cette surface, une force de 1 N (newton).
– v. Unités, unités de pression
– a. Pascal

Pascal (triangle de -) ou triangle arithmétique: tableau de nombres disposés en triangle dont chacun est la somme des deux nombres du dessus; nombreuses utilisations en dénombrement.
– v. Triangle de Pascal, binôme de Newton
– a. Pascal's triangle

Passif: dans un bilan, colonne de nombres qui témoignent de l'origine des ressources de l'entreprise.
C'est ce que possède l'entreprise selon sa provenance.
– ex. Le capital est mis au compte du passif.
– mnémo: savoir d'où vient l'argent (d'où viennent les fonds) est un fait du passé.
– v. Actif, débit, crédit, balance, bilan
– a. Liabilities and equity (dettes, engagements et fonds propres).

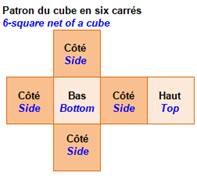Patron ou modèle ou développement d'un solide: dessin qui permet de confectionner un solide (polyèdre) par découpage, assemblage et collage.
– ex. Le patron du cube consiste en six carrés contigus dessinés en croix.
Très utilisé dans les origamis, art japonais du papier plié.
– v. Patron du cube, du cylindre
– a. Net of a polyhedron

Pavage: sorte de carrelage.
Recouvrement d'une surface par des figures données, appelées pavés ou tuiles.
Remplissage de l'espace complet par des polyèdres.
Il existe seulement 17 pavages réguliers du plan (sortes de frises).
– syn. Maillage, frise, dallage, carrelage
– ex. Polygones.

Pavé: Voir parallélépipède

Pédal: le triangle pédal des médianes d'un triangle est le triangle dont les sommets sont les milieux des côtés.
D'une manière générale, le triangle pedal d'un point P a pour sommets les pieds des perpendiculaires menées du point P sur les côtés du triangle.
– propriété (selon le théorème de Carnot): BA'² + CB'² + AC'² = A'C² + B'A² + C'B².
– a. A pedal triangle is obtained by projecting a point onto the sides of a triangle.

Pentagone: polygone à 5 côtés.
Chacun des angles d'un pentagone régulier vaut 108°.
Dans un pentagone régulier, on peut dessiner une étoile à cinq branches.
Le nombre d'or se niche dans cette figure: rapport diagonale sur côté.
Douze pentagones réguliers réunis forment le dodécaèdre.
Un pentadécagone possède quinze côtés.
– v. Pentagone
– a. Pentagon

Pentagramme ou pentagone étoilé: dessin qui représente une figure à cinq éléments, telle une étoile à cinq branches.
Principalement utilisé en ésotérisme.
– v. Pentagramme et nombre d'or
– a. Pentagram: the shape of a five-pointed star polygon

Pentamino: figure formée de cinq carrés identiques assemblés.
Il y a douze pentaminos. Famille des polyominos
Objet de récréations mathématiques
– a. Pentomino, pentominoes

Pente ou coefficient angulaire ou coefficient directeur: caractérise l'inclinaison d'une droite.
Correspond à la tangente de l'angle entre une droite et l'axe des x.
Coefficient a de l'équation de la droite y = ax + b
Variation de y pour un incrément unité en x:
– v. Pente, équation de la droite, dérivée
– a. Slope, gradient: a number that describes both the direction and the steepness of the line

Percolation (théorie de la -)**: imaginez des poussières aléatoires qui se collent (percolent) dès qu'elles en rencontrent d'autres …
Phénomène lié à un écoulement aléatoire avec agglutinement des particules à partir de semences initiales.
Imaginez le chemin qu'emprunte l'eau qui coule à travers les matériaux poreux ou les grains de café: origine du nom de la théorie.
La théorie de la percolation décrit le comportement d'un graphe lorsque des nœuds ou des arcs sont ajoutés.
Utilisation pour la modélisation des phénomènes naturels en milieu aléatoire.
– ex. quels sont les canaux d'écoulement de l'eau dans un matériau poreux.
– v. Percolation / Hugo Duminil-Copin / Conjecture des lits superposés
– a. Percolation theory

Perfectoïde (espace -)**: espace topologique spécial, étudié dans le cadre du programme Langlands tentant de connecter la théorie des nombres et la géométrie. Notion introduite par Peter Scholze en 2014, University of California, Berkeley.
– v. Théorie de représentations, mathématiques condensées
– a. Perfectoid space

Mode de représentation géométrique de nature fractale des nombres p-adiques comme les nombres réels sont représenté par la droite des réels. Les mathématiciens cherchent de tels objets géométriques représentant les nombres. Laurent Fargues et Jean-Marc Fontaine s'intéressent à des courbes dont les points représentent un anneau p-adique (p-adic ring).

Périmètre: longueur d'une courbe fermée.
Le périmètre du carré vaut quatre fois la longueur de son côté (P = 4c);
Le périmètre du cercle est sa circonférence (P = 2pR = pD).
– v. Périmètre, aire, volume
– a. Perimeter

Période: en physique, intervalle de temps entre deux répétions d'un même phénomène.
– v. Ondes périodiques
– a. Period

Périodique (fonction -): fonction qui se répète régulièrement lorsque x croit d'une quantité finie appelée période de la fonction: f(x + p) = f(p)
– syn. Cyclique
– ex. Les fonctions sinus et cosinus sont périodiques.
– a. Periodic function: a function that repeats its values at regular intervals

Périodique (nombre -) ou nombre à développement périodique: nombre rationnel dont les chiffres, à partir d'un certain rang, se répètent indéfiniment.
– v. Nombres périodiques, vinculum (barre de surlignement de la période), virgule décimale
– a. Periodic numer: a number whose decimal notation is repeating.

Période d'un nombre rationnel: groupe de chiffres qui, dans le développement décimal périodique d'un nombre rationnel, se répètent indéfiniment, soit à partir de la virgule, soit à partir d'une décimale donnée.
– ex. 1/7 = 0,142857 142 857 …
La période est "142857" et sa longueur est 6.
– v. Vocabulaire des nombres périodiques
– a. Repetend

Permutation: synonyme d'inversion, d'interversion.
– ex. 132 est une permutation de 123.
Avec n éléments, la quantité de permutations possibles est n! = 1 x 2 x 3…x n (factorielle n).
C'est aussi la quantité de manières de ranger n objets de toutes les façons imaginables.
– v. Permutations, combinatoire, subtitution
– a. Combination: any of the ways we can combine things, when the order does not matter. When the order does matter, it is a permutation.

Permutation circulaire: pour passer d'une configuration à la suivante, chaque objet est glissé d'un cran vers la droite (ou vers la gauche), le dernier passant en premier (ou l'inverse).
– ex. 1234 => 2341 => 3412 => 4123 => 1234
– note: un décalage d'un nombre binaire vers la droite correspond à une division par 2. Réalisation avec un simple registre à décalage. Idem pour la multiplication par 2.
– v. Nombre 1,01 10⁴⁰ (cas singulier).
– a. Cyclic permutation

Permutation figurée: sur une grille carrée, disposition telle qu'il n'y a jamais deux éléments sur une même ligne ou une même colonne. Illustration
Il y a 4! = 24 permutations figurées d'ordre 4.
– histo. Les permutations figurées ont été introduites en 1883 par le mathématicien Édouard Lucas.
– v. Permutations figurées, Carré latin
– a. Lucas permutation

Permutation à motif: permutations qui ne contiennent pas un motif spécifié.
– v. Permutations à motif
– a. Permutation pattern

Permutoèdre**: polyèdre dont les sommets sont toutes les permutations de k nombres.
Octaèdre tronqué: coordonnées des sommets = les 24 permutations de (-2, -1, 0, 1, 2).
Polytopes à permutation.
– a. Permutohedron

Perpendiculaire: qui fait un angle droit (90°).
– ex. Sur un voilier, la bôme est perpendiculaire au mât.
– v. Types de perpendiculaires, orthogonal, subtilité de langage, éléments de base de la géométrie
– a. Perpendicular, normal, orthogonality

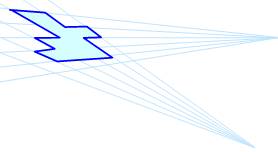
Perspective: manière de visualiser un objet en 3D sur une feuille de papier en 2D.
Il existe trois cas de dessins en perspective: un point, deux points ou trois points.
Les lignes bleues sur l'illustration sont les lignes de fuite.
La ligne horizontale représente l'horizon.

Perspective parallèle, cylindrique ou axonométrique: perspective centrale dont le centre O est rejeté à l'infini. C'est donc, une projection sur le plan P parallèlement à une direction donnée D. Si D est orthogonale à P, c'est une axonométrie orthogonale, sinon elle est oblique ou cavalière.
– note: il existe une grande variété de perspectives parallèles: cavalière, orthogonale, normale, equiangulaire, etc. Voir Axonometry – Wikipedia
– a. Axonometry

Perspective cavalière: manière classique de représenter les solides en géométrie; telle qu'elle conserve les parallèles. C'est une perspective parallèle.
Point de vue rejeté à l'infini.
– v. Perspective cavalière
– a. Oblique projection

Perspective centrale (ou projection centrale): Soit O un point fixe du plan, le centre de projection. Il représente l'œil de l'observateur. Un plan P, le plan du tableau et un point M de l'espace (hors du plan parallèle à P en O). Alors, l'image de M est le point d'intersection de la droite OM avec le plan P.

PGCD: plus grand commun diviseur.
– notation: PGCD(a, b) ou simplement: (a, b).
– ex. PGCD(10,14) = (10, 14) = 2.
Si le PGCD de deux nombres est égal à 1, ces nombres sont premiers entre eux ou étrangers
– ex. PGCD(14, 35) = 1.
– v. PGCD, PPCM, nombres premiers entre eux, algorithme d'Euclide
– a. Greatest commun divisor (gcd), parfois igcd pour gcd of integers.

Phrase mathématique: synonyme d'expression mathématique.
– a. Mathematical sentence, mathematical expression

Pi (p): constante qui vaut 3, 141 592 65… » 355/113 » 22/7.
Dans un cercle, ratio circonférence sur diamètre (C = p D) ou aire sur carré du rayon (A = p R²).
Constante d'Archimède, nombre irrationnel et transcendantal.
– On dit (disait ?) souvent trois quatorze cent seize pour la 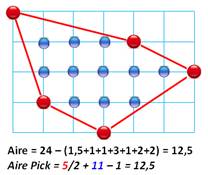valeur approchée: 3,1416.
– v. Pi = 3,14… , Tau = 2Pi = 6, 28 …
– a. Pi (prononcer: paille): the circumference to diameter ratio of a circle

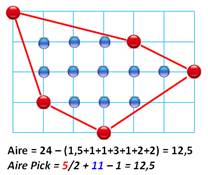
Pick (formule de -): l'aire d'un polygone dessiné dans une grille (un quadrillage) est donné par cette formule: A = P/2 + Q – 1; avec P la quantité de points situés sur le pourtour (la ligne polygonale); et Q la quantité de points situés à l'intérieur du polygone (Illustration).

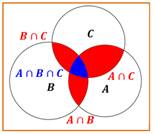PIE: Principe d'Inclusion-exclusion en dénombrement: permet d’exprimer le nombre d’éléments (ou cardinal) d'une réunion finie d'ensembles finis en fonction du nombre d'éléments de ces ensembles et de leurs intersections.
– formule pour trois ensembles (les traits représentent le cardinal de l'ensemble).
"Le tout = les trois – leurs intersections (rouge) + l'intersection des trois (bleue)"
– a. Inclusion-exclusion principle

Pied d'une hauteur: extrémité de la hauteur où se trouve l'angle droit.
L'autre extrémité étant un des sommets du triangle.
Le triangle ayant les pieds des hauteurs pour sommets est le triangle orthocentrique ou orthique.
– a. the foot of the altitude, the feet of the altitudes; orthic triangle or altitude triangle

Pile ou face (jeu de -): jeu avec des pièces de monnaie dont l'issue est pile ou face.
– v .Pile ou face, lancer de dés, probabilités et statistiques
– a. Heads or tails / cross or pile (R.-U)

Pincement: terme technique indiquant que deux roues ne sont pas parallèles mais se "croisent" en avant du véhicule.
En arrière, c'est l'ouverture.
– v. Pneu, angle
– a. Toe angle, positive toe = toe in = pincement and negative toe = toe out = ouverture.

Piphilologie: art de réciter les chiffres du nombre Pi.

Pixel: élément le plus fin d'une image; le plus petit élément de teinte homogène d'une image enregistrée en photographie, télévision, télécommunications, informatique.
– ex. Un téléviseur 4k a une définition de huit millions de pixels (3 840 x 2 160 = 8 294 400 pixels).
– v. Pixel
– a. Pixel

Plafond: fonction qui arrondi un nombre par le haut.
– notation:
– v. Arrondi, plancher, plafond
– a. Anglais: ceil

Plan: image de la surface d'un miroir, d'un billard ou d'une piscine.
Équivalent à une feuille de papier posée à plat de dimensions illimitées.
Surface telle que si elle contient deux points d'une droite, elle contient la droite toute entière.
Espace de dimension deux, noté .
Il suffit de trois points pour définir un plan.
Deux plans peuvent être parallèles, perpendiculaires ou sécants.
– v. Plan
– a. Plane: a flat, two-dimensional surface that extends indefinitely.

Planaire (graphe -): un graphe dont aucunes des arêtes ne se coupent en le dessinant sur un plan.
– ex. Problème des trois maisons
– a. Planar graph

Plancher et plafond: fonction qui arrondi un nombre par le bas ou par le haut.
– notation:
– v. Arrondi, plancher et plafond
– a. Anglais: floor

Plat (angle -): angle de 180° ou p radians.
Ses côtés forment une droite.
– v. Types d'angles
– a. Strait angle: 180° in measure

Plein (angle -): angle de 360° ou 2p radians.
– v. Types d'angles
– a. Complete angle: 360° in measure

Plongement**: structure mathématique qui est contenue dans une autre.
– a. Embedding ou Imbedding

P-liste: en dénombrement, quantité de possibilités de choix comme avec un digicode.
Chacun des chiffres est choisi indépendamment des autres.
Arrangement avec répétition.
La quantité de possibilités pour n digits de p chiffres est n^p.
– ex. 4 digits de 10 chiffres donnent un choix de 4¹⁰ = 1 048 576 codes différents.
– v. Types de dénombrement

Étant un ensemble à n éléments, on appelle p-liste de E toute suite (x₁, x₂... , x_p) où chaque x_k est élément de E. Il y a n^p p-listes d'un ensemble à n éléments.

PMI: proof by mathematical induction: démonstration par induction (mathématique).

Podaire d'une courbe * par rapport à un point O: lieu des projections de O sur les tangentes à la courbe
– a. Pedal curve

Poids: proche, mais à ne pas confondre avec la masse.
Le poids est une force subie du fait de l'attraction par la Terre.
C'est grâce à ce phénomène que tout le monde tient debout sur le globe terrestre (comme attiré par le centre de la Terre).
Force égale au produit de la masse d'un corps par l'accélération de la pesanteur
– unité SI: newton (N)
– v. Pesanteur, forces
– a. Weight

Poincaré: Henri Poincaré et un mathématicien français (1854), père de la topologie.

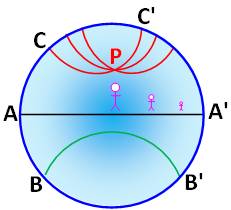
Disque de Poincaré (illustration): pour emprunter le plus court chemin, un habitant de ce monde réduit aura toujours tendance à passer par le centre du disque, où la "température" élevée lui permet de faire des pas de géant.
La simplicité de la métrique permet d’expliciter les droites géodésiques: ce sont les arcs de cercle orthogonaux au (type CC') bord du disque. Par le point P passent donc une infinité de “droites” ne coupant pas la droite AA'.

– v. Cercle ou disque de Poincaré, cercle de Esher
– a. Poincaré disk model or conformal disk model

Conjecture de Poincaré: la sphère (topologique) est le seul espace tridimensionnel fermé dépourvu de trous.
Émise en 1904 par Henri Poincaré et prouvée en 2002 par Grigori Perelman.
– v. Conjecture de Poincaré
– a. Poincaré conjecture

Point: élément géométrique qui n'a pas d'étendue.
Intersection de deux lignes: point d'intersection. Intersection de trois lignes ou plus: point de concours.
Une marque sur une ligne ou l'extrémité d'un segment.
Objet sans dimension ou ligne de longueur nulle.
La ligne à une dimension 1, le point est de dimension 0.
Quelques points particuliers: extrémités d'un segment, sommet d'une figure, point d'intersection de deux courbes; points de concours de plusieurs droites, points cocycliques ….
Dans un repère plan (2D), il faut deux coordonnées (x, y) pour positionner un point; il en faut trois (x, y, z) dans l'espace (3D).
Deux points définissent une droite; trois points définissent un cercle; quatre points pour un quadrilatère; cinq points pour une conique.
– v. Types de points (sommet, milieu, centre …)
– a. Point

Points de suspension: un nombre décimal suivi de points de suspension indique que toutes les décimales indiquées sont exactes, non-arrondies.
– notation:
– a. trailing dots.

Pointeur: en informatique, indique l'adresse mémoire d'une donnée.
Notion d'adressage indirect: on va chercher une donnée qui servira d'adresse pour en trouver une autre.
– notion proche: index, indice, itération
– a. Pointer: an object in many programming languages that stores a memory address.

Pointeur: flèche (ou uatre symbole) qui court sur l'écran selon la position de la souris.

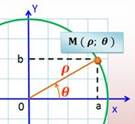
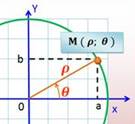
Polaires (coordonnées): représentation en angle(s) et distance sur un système d'axes; dans le plan et dans l'espace .
– v. Coordonnées polaires
– a. Polar coordinate system

Polaire (angle -): angle q dans le système de coordonnées polaires.
Quant à c'est le rayon –vecteur.
– Syn. Azimut;
– a. Angular coordinate, polar angle, or azimuth

Pôle et polaire*: la polaire d'un point par rapport à deux droites sécantes du plan est une droite définie par conjugaison harmonique.
Généralisation aux cercles et aux coniques.
– v. Éléments de base de la géométrie (polaire et podaire)
– a. Pole and polar

Transformation par polaires réciproques**: transformation associant à une courbe une autre courbe construite à l'aide des droites tangentes à la première. La courbe image s'appelle la courbe duale de la courbe de départ.
– a. Reciprocal polar of a curve

Pôle de l'inversion* synonyme de centre de l'inversion.
– v. Inversion.

Polyabolo ou polytan: sorte de polyomino mais avec des triangles isocèles rectangles identiques.
Les quatre tiabolos (Illustration).
– v. Tangram
– a. Polyabolo

Polyamant: sorte de polyomino mais avec des triangles équilatéraux identiques.
Quantités: 1triamant, 3 tétramants, 4 pentamants, 12 hexamants, …
– a. Polyamond

Polychore ou 4-polytope*: figure 4D dont la surface tridimensionnelle est composée de plusieurs polyèdres.
Avec 16 cellules, c'est un hyperoctaèdre.
– a. Polychoron

Polycube: sorte de polyomino en trois dimensions.
Assemblage de cubes identiques par au moins une face.
Quantités: 2 tricubes, 4 tétracubes, 29 pentacubes, 166 hexacubes, …
– a. Polycube

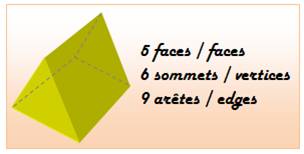
Polyèdre: solide limité par des faces planes, des polygones; vient du grec polus nombreux et edra face.
– v. Polyèdres
– a. Polyhedron

Polyèdre régulier: les faces polygonales sont toutes égales; il en existe seulement cinq convexes:
– v. Tétraèdre, cube, parallélépipède, octaèdre, dodécaèdre, icosaèdre.
– a. Regular polyhedron

Polyèdre régulier étoilé: les faces d'un polyèdre régulier sont prolongées jusqu'à ce qu'elles se coupent et forme un nouveau polyèdre (Illustration).
– a. Star polyhedon

Polyforme: généralisation des polyominos.
Assemblages de formes identiques avec au moins un élément commun.
Parmi eux, les polyominos (carrés), les polyamants (triangles équilatéraux), les polycubes (cubes), les polyhex (hexagones), les polypons (triangles 30-30-120), les polykites (cerfs-volants), etc.
– a. Polyform

Polygonale (ligne -) ou ligne brisée: suite de segments, dans le plan ou dans l'espace, reliés l'un après l'autre par leurs extrémités.
Un polygone est une ligne polygonale fermée.
Le théorème de Jordan dit qu'une courbe fermée divise le plan en exactement deux régions: un intérieur et un extérieur.
– a. Polygonal chain.

Polygone: ligne brisée fermée.
Le plus petit a trois côtés, c'est le triangle.
Le quadrilatère en a quatre.
Quelques autres: pentagone (5), hexagone (6), heptagone (7), octogone (8), ennéagone (9), décagone (10), dodécagone (12), icosagone (20), hectogone (100), …
– v. Polygones, quadrilatères
– a. A polygon is any shape whose sides are all straight. Every polygon has three or more sides

Polygone régulier: dont tous les côtés ont même longueur et les angles sont aussi égaux.
On dit: côtés congruents et angles congruents.
Le polygone régulier est à la fois équilatéral et équiangle.
– a. Regular polygon

Polygone régulier étoilé: Polygone croisé dans lequel chaque côté coupe tous ses côtés non adjacents.
– v. Étoile à cinq branches, étoile à six branches, hexagramme
– a. Star polygon

Polygone rectilinéaire: tous ses angles valent 90° (Illustration)
– a. Rectlinear polygon

Polygone isothétique: dont les côtés sont inscrits dans le maillage créé par deux faisceaux de droites concurrentes. (Illustration)
Les polygones isothétiques sont utilisés en géométrie algorithmique.
– v. Isothétique
– a. Isothetic polygon

Polygone auto-évitant (PAE): polygone construit sur un réseau et dont les côtés ne se croisent jamais.
Le périmètre constitue un chemin auto-évitant.
– v. Polygone auto-évitant
– a. Self-avoiding polygon (SAP)

Polygone convexe: toute la figure est située d'un même côté d'une ligne passant par un des côtés, quel que soit le côté; sinon il est concave.
– a. Convex polygon

Polygone réfléchi: polygone replié le long d'une ligne passant par deux sommets.
Ils ont la propriété de paver le plan pour un nombre impair de côté (>3)
– v. Polygones réfléchis
– a. Reflecting a polygon

Somme des angles du polygone: vaut 180° x (n – 2), avec n le nombre de côtés.

Polygone sphérique: polygone dessiné sur une sphère.
Ses arêtes sont des arcs de grands cercles.
On aura des triangles sphériques, des quadrilatères sphériques, des pentagones sphériques, etc.
– a. Spherical polygon: a figure on the surface of a sphere which is formed by the arcs of great circles.

Polygramme régulier: polygone croisé. Sorte d'étoiles
Figure géométrique formée par n sommets répartis régulièrement sur un cercle et dont les côtés s’obtiennent en reliant le sommet k au sommet k+e, où e est l’écart entre les sommets reliés les uns à la suite des autres
– v.Étoiles à cinq branches ou pentagramme
– a. Polygram, pentagram

Source image: Polygramme par Sebastien Reb

Polynôme: somme algébrique à plusieurs termes (a + 6b³ – 17c⁵ …).
Combinaison linéaire de puissances d'une variable: .
n est le degré du polynôme (si ).
Types de polynômes: monôme (4x²y), binôme (2x³ + 1), trinôme (2x – 3y² + 3) et plus …
La division par une variable est exclut: 7 / x² n'est pas un polynôme.
– v. Polynôme
– a. Polynomial

Polynôme constant: dont tous les coefficients sont nuls à l'exception éventuelle du coefficient constant.
Son degré est alors d'au moins 1.
– a. Constant polynomial
Polynôme nul: dont tous les coefficients sont nuls, y compris le coefficient constant.
– a. Zero polynomial
Polynôme primitif: le PGCD des coefficients vaut 1.Les coefficients sont premiers entre eux.
– a. Primitive polynomial
Polynômes constants, linéaires, quadratiques ou cubiques: de degré 0, 1, 2 ou 3.
– a. Constant polynomials, linear polynomials, quadratic polynomial or cubic polynomials
Polynômes homogène: chaque terme est de même degré cumulé.
– ex. x³y² + 5x²y³ + x⁵ est homogène de degré 5.
– a. Homogeneous polynomial

Polynôme unitaire (ou polynôme normal ou polynôme monique): de la forme xⁿ + a_n-1x^n-1 + … + a₀.
Une seule variable x et le premier coefficient est égal à 1 (le coefficient de x de plus grand degré est 1; ou encore: le coefficient du monôme dominant est égal à 1).
– a. Monic polynomial.

Polynôme unitaire à coefficients entiers: tous les a_i sont des nombres entiers. Leurs solutions réelles sont des nombres dits "entiers algébriques".

Polynôme symétrique: polynôme qui reste inchangé en inversant ses variables.
– ex. x² + y² + z², x²y + xy²
– v. Polynôme symétrique
– a. Symmetric polynomial

Polynôme symétrique élémentaire: polynôme symétrique du premier degré.
– ex. x+y+z, xyz, xy + yz+ zx
Théorème fondamental des fonctions symétriques: tout polynôme symétrique est décomposable de façon unique en une fonction polynomiale de polynômes symétriques élémentaires. Ceux-ci sont donc les briques fondamentales de l'algèbre des polynômes symétriques.
– ex. x² + y² = (x + y)² – 2xy, x³ + y³ = (x + y)³ – 3(x + y)xy
– v. Polynôme symétrique élémentaire, théorème fondamental de l'arithmétique
– a. Elementary symmetric polynomial

Polynôme hyperbolique: polynômes à coefficients réels dont toutes les racines sont réelles.
– v. Hyperbolique

Polynômes inversible**: P est inversible s'il existe un polynôme Q tel que P·Q = 1

Polynômes irréductibles**: polynômes non factorisables; jamais produit de deux polynômes.
P est un polynôme irréductible s'il n'est ni nul, ni inversible, ni produit de deux polynômes non inversibles.
– ex. En mod 2 (F₂), x² + 1 = (x + 1)² est réductible; mais x² + x + 1 ne l'est pas.
– v. Corps de Galois, polynômes irréductibles sur Fp
– a. Irreductibl polynomial: a polynomial that cannot be factored into the product of two non-constant polynomials.

Polyomino: assemblage de carrés.
Le domino est formé à partir de deux carrés assemblés.
Le pentomino est formé de cinq cubes. Ils sont douze.
Objet de puzzles: former un rectangle ou une forme donnée avec la totalité des pentominos.
– v. Polyomino
– a. Polyomino

Polytope* polyèdre de dimension 4 ou plus.
Hyper-volume, comme l'hyper-sphère.
– v. Polytope
– a. Polytope

Pondération: synonyme de coefficient; sorte de "poids" donné à une variable, à une branche d'un graphe …
– v. Barycentre, moyenne pondérée
– a. Weighting

Pont aux ânes: démonstration que tout le monde devrait connaître.
– ex. les angles opposés aux côtés égaux d'un triangle isocèle sont égaux.
Aussi le théorème de Pythagore.
– a. Pons asinorum

POO (programmation orientée objet): elle consiste à définir des entités (objets) qui possèdent des propriétés permanentes, un comportement et des possibilités de dialogue externe.
Ces entités, définies une fois pour toute, en font profiter d'autres par procédé d'héritage.
Ce type de programmation facilite grandement la structuration des logiciels.
Pour être pleinement efficace, elle nécessite un environnement de programmation intégré (IDE).
– v. Fonction informatique
– a. Object-oriented programming (OOP)

Population: en statistique, ensemble du domaine étudié.
Un échantillon de 20 pièces sur une population de 100 fabriquées
– syn. Univers statistique.
– v. Statistique
– a. Population: the entire set of items from which data can be selected.

Poset ou ensemble partiellement ordonné: ensemble muni d'une relation d'ordre qui indique que pour certains couples d'éléments, l'un est plus petit que l'autre. Tous les éléments ne sont pas forcément comparables, contrairement au cas d'un ensemble muni d'un ordre total.
– a. Partially ordered set or poset for short: arrangement such that, for certain pairs of elements, one precedes the other.

Positif (nombre -): nombre réel supérieur à zéro.
Nombre accompagné du signe +, souvent omis car implicite par convention.
Ensemble des entiers positifs: .
– v. Relatif, négatif, signe
– a. Positive real numbers

Positif (rotation): sens positif dans le sens contraire des aiguilles d'une montre.
– v. Conventions pour les angles de rotation

Position (numération de -) ou notation positionnelle: système de numération pout lequel la position des chiffres importe.
Dans le système décimal, les chiffres "pèsent" des puissances de 10.
– v. Numération
– a. Positional notation, place-value notation, positional numeration system

Méthode de la fausse position: procédé de calcul astucieux évitant notamment le calcul avec les fractions
– v. Exemple d'utilisation
– a. Regula falsi, method of false position

Postulat: affirmation tenue pour vraie, avec intention de le démonter ultérieurement.
Entre hypothèse – affirmation temporaire – et axiome – affirmation non démontrée.
– étym. Vient du latin postulare demander, idée de quelque chose que l'on demande d'accepter.
– v. Démonstration, théorème, axiome, hypothèses, etc.
– v. Cinquième postulat d'Euclide: " deux droites parallèles ne se rencontrent jamais".

Pou de Mandelbrot ou ensemble de Mandelbrot*: une sorte de fractale dont l'équation est très simple et le dessin si riche en autosimilarités.
– v. Fractales de Julia-Mandelbrot
– a. Mandelbrot set

Pourcentage: rapport ramené à une base de 100 de manière à faciliter les comparaisons.
– notation: % et parfois p.c. On a aussi pour mille: ‰
– ex. 3 sur 25 = 3/25 = 0,12 est la même chose que 12%.
– v. Pourcentage, rapport, proportion, prorata
– v. Fraction, règle de trois, multiplication
– a. Percent proportion, pourcentage. 5% se lit: faille ve pe sente et non pas père sent à la française
ou selon la phonétique internationale:

Exemples de calculs
Je viens d'obtenir une augmentation de 5% alors que mon salaire est de 2000 euros.
Mon augmentation: 2000 x 5 / 100 = 100 euros.
Mon nouveau salaire: 2000 + 100 = 2100 euros.
Calcul direct de mon nouveau salaire: 2000 x 1,05 = 2100 euros.

J'ai une réduction de 5% sur mes achats de 100 euros.
Ma ristourne: 100 x 5% = 100 x 5 / 100 = 5 euros
Mon net à payer: 100 – 5 = 95 euros

Pourcentile: angliscime (à éviter) pour centile: partage d'une population en un certain nombre de centièmes de parties d'un même effectif.
– v. Quartile
– a. Percentile

PPCM: Plus petit commun multiple.
– notation: PPCM(a, b) = [a, b].
– ex. PPCM (2, 6, 10) = [2, 6, 10] = 2 x 3 x 5 = 30.
– v. PPCM, PGCD, nombres premiers entre eux, algorithme d'Euclide
– a. Least commun multiple (lcm), parfois ilcm pour lcm of integers.

ppp: points par pouce, équivalent français de dots per inch, dpi.

ppm: partie par million (10^-6).
ppb par milliard.
ppb par 10¹².
ppq par 10¹⁵.
– v. ppb, ppt, ppq

Précession* mouvement conique décrit autour d'une position moyenne par l'axe d'un corps animé d'un mouvement gyroscopique.
– ex. L'axe de rotation terrestre subit une précession.
L'axe des pôles décrit un cône.
La précession du plan d'oscillation du pendule de Foucault, précession des équinoxes.
– a. Precession: a change in the orientation of the rotational axis of a rotating body.

Précision (numérique): la précision d'une valeur numérique est le nombre de chiffres utilisés pour exprimer cette valeur. Les chiffres indiqués sont réputés être exacts.
C'est aussi la quantité de décimales.
Le dernier chiffre représente l'arrondi.
– ex. 85,124 euros à la pompe sera arrondi à deux décimales: 85,12 euros.
Écrire 5,00 veut dire que la valeur se situe entre 4,995 et 5,005 (Illustration: nombre à droite et sa valeur arrondie à deux décimales ou trois chiffres significatifs).
– a. Significant figures: the number of digits that carry real information about a measurement

Précision (métrologie): témoigne de l'aptitude à effectuer des mesures fines.
– ex. Un ampèremètre de 1mA de précision. Il donnera une quantité de milliampères, sans que nous soyons assurés que cette mesure soit exacte.
– attention ! Ce mot n'existe plus en métrologie: on parle plutôt de résolution, exactitude et fidélité.
– v. Incertitude et précision, résolution, sensibilité, exactitude, fidélité
– a. Accuracy and précision

Prédécesseur: qui est avant.
– ex. Le prédécesseur de 5 est 4.
– a. Predecessor, successor

Prédicat**:
Prédicat en grammaire: mot compliqué pour nommer une phrase sans son sujet.
Partie de la phrase (ou clause) qui dit quelque chose à propos du sujet, autrement qu’en le nommant.
– a. Predicate: everything in a standard declarative sentence except the subject.

Prédicat en logique: expression énonçant une propriété à propos d'une ou plusieurs variables
En donnant une valeur aux variables, le prédicat devient une proposition vraie ou fausse.
– ex. prédicat sur P(x): x > 5,
x est la variable et > 5 est le prédicat
Avec x = 7, P(x) devient proposition dont la valeur est vraie.
– ex. E(x, y): x = y; X(a, b, c): a + b + c = 0; M(x, y): x est marié à y

Une variable peut être quantifiée par les quantificateur universel ("pour tout" ) ou existentiel ("il existe" ). Le prédicat devient alors une proposition.

– v. Logique en bref, unaire (prédicat -), logique, implication, copule
– a. Prédicate: propertie, additional information to better express the subject of the sentence. A quantified predicate is a proposition , that is, when you assign values to a predicate with variables it can be made a proposition.

Prédicats (calcul des -)**: proche de calcul propositionnel avec des variables.
Le calcul des prédicats du premier ordre, ou logique du premier ordre comporte deux parties: la syntaxe (vocabulaire) et la sémantique (interprétation).
– v. Logique en bref
– a. First order logic

Prédiction: calculer de nouvelles valeurs à partir d'un modèle de la réalité ou à partir du fruit de l'expérience.
L'extrapolation et l'interpolation sont des outils de prédiction.
– a. Prediction, extrapolation, interpolation

Pré-image: parfois utilisé à la place d'antécédent.
Pré-image de x par une application, élément de l'ensemble de départ dont l'image est x.

Premier: celui qui est en tête; adjectif numérique ordinal.
– v. Premier, deuxième et second
– a. First

Premier (nombre -): nombre divisible que par 1 par lui-même.
Nombre géométrique dit BARRE, car on ne peut pas les "plier"; on ne peut pas réaliser de surface.
– ex. 2, 3, 5, 7, 11 ….
Seul 2 est un premier pair, tous les autres sont impairs.
Par convention, 1 n'est pas premier.
Les autres nombres (non-premiers) sont dits composés.
– v. Nombre premier, barre magique des nombres premiers, largueur du rectangle.
– a. Prime number

Premiers entre eux (ou étrangers ou copremiers): nombre qui n'ont aucun diviseur en commun.
Leur PGCD est égal à 1.
– ex. 3 et 5 ou 15 (= 3 x 5) et 77 = (7 x 11).
– v. Nombres premiers entre eux / Identité de Bézout
– a. Coprime, mutually prime or relatively prime.

Premier degré (équation du -): équation du type ax + b = 0.
– v. Équation du premier degré
– v. Polynôme, second degré, équation de la droite, affine et linéaire, mouvement uniforme.

Prémisse: idée de point de départ d'un raisonnement.
Proposition d'où découle une conséquence.
– a. Premise ou premiss: a true or false statement that helps form the body of an argument

Prémisse: en logique, chacune des deux premières propositions d'un syllogisme: la majeure et la mineure.
– v. Antécédent
– a. Premise, syllogism: a syllogism arises when two true premises (propositions or statements) validly imply a conclusion

Preuve: fait ou raisonnement qui établit la véracité d'une proposition.
Méthode de vérification d'un calcul, d'un théorème.
Parfois: vérification d’une opération de calcul, qui se fait par l’opération opposée (un addition pour vérifier la soustraction, par exemple).
– a. Proof

Preuve par neuf: preuve consistant à refaire le calcul en modulo 9, ce qui simplifie le calcul.
– v. Preuve par neuf
– a. Casting out nines (éliminer ou ignorer les 9)

Preuve par intimidation: preuve qui contient des arguments du genre, "on peut facilement montrer que …". Lesquels incitent le lecteur à croire sur parole l'auteur de la démonstration.
– a. Proof by intimidation: "It is self-evident that...", "The proof is left as an exercise for the reader".

Primaire (nombre - ) ou puissance première: nombre premier ou puissance de premier.
– ex. 4 = 2²; 625 = 5⁴; 12 = 3 x 4 n'est pas primaire
– v. Nombre primaire, diviseur primaire
– a. Prime power: a positive integer power of a single prime number

Primarité ou primalité (test de - ) Test qui cherche à déterminer si un nombre est premier ou composé.
– v. Primalité - Index
– a. Primality test

Note: primarité au sens usuel: caractère, manifestation de la fonction primaire chez l'individu. Avec le mot primalité (primality en anglais), on cherche sans doute à s'écarter du sens péjoratif de primarité. Le Wiktionnaire renvoie au mot primalité: en mathématiques, état d’un nombre premier.

Primitive* fonction inverse de la dérivée.
– ex. Soit la distance parcourue en fonction du temps et la vitesse en fonction du temps: la vitesse est la dérivée de la distance et la distance est la primitive de la vitesse; même chose entre vitesse et accélération.
– v. Intégrale, Accélération, dérivée, dérivées usuelles, primitives usuelles
– a. Antiderivative

Primorielle: factorielle avec les nombres premiers seulement.
– ex. P(7) = 2 x 3 x 5 x 7 = 210.
– v. Primorielle
– a. Primorial

Principe: proposition admise comme base d'un raisonnement.
Une source, un fondement, une vérité première d'idées ou d'autres choses.
– v. Postulat.
– a. Principle: A fundamental assumption or guiding belief. A rule or law of nature,

Principe des tiroirs: s'il y trois chaussettes pour deux tiroirs, l'un des tiroirs contiendra au moins deux chaussettes.
– v. Principe des tiroirs
– a. Pigeonhole principle

Principe du tiers exclus: une proposition est vrai ou fausse, il n'y pas de troisième possibilité.
– v. Tiers eclu
– a. Law of excluded middle, principle of excluded middle

Principe d'Archimède: Un corps placé dans l'eau subit une poussée vers le haut qui est égale en force au poids de l'eau que l'objet a déplacé.
– v. Principe d'Archimède
– a. Archimedes's principle

Priorités (règle des -): façon de calculer en suivant les conventions d'écriture des expressions littérales:
1) calcul à l'intérieur des parenthèses et
2) effectuer puissances, multiplications puis additions.
– v. Calculs algébriques, priorité des opérations (PEMDAS …)
– a. Order of operation, BEMDAS

Prisme: sorte de "cylindre", mais à facettes, à bases polygonales
Les deux bases, haute et basse, sont parallèles et superposables.
Lorsque les faces latérales sont perpendiculaires aux bases, le prisme est droit.
Lorsque les faces latérales sont des carrés et les bases des polygones réguliers, le prisme est uniforme.
– def. Polyèdre constitué par deux bases polygonales superposables situées dans deux plans parallèles et par des parallélogrammes (pour les prismes inclinés) ou des rectangles (pour les prismes droits) joignant les bases.
Volume engendré par un polygone qui se déplace le long d'une génératrice, comme si on donnait de l'épaisseur au polygone.
– v. Prisme
– a. Prism: a solid geometric figure whose two ends are similar, equal, and parallel rectilinear figures, and whose sides are parallelograms. Right prism, uniform prism, oblique prism

Prismatoïde: polyèdre dont les sommets sont placés sur deux plans parallèles: pyramides, prismes, antiprismes, parallélépipèdes, rhomboèdres, cubes …
– a. Prismatoid

Prismoïde: prisme où les deux bases ont le même nombre de côtés, mais inégaux.
– a. Prismoid: a body like a prism, in which the end faces have the same number of sides but are not equal.

Probabilité: nombre qui qualifie la possibilité qu'un événement se produise ou non.
Résultat de la division du nombre de cas favorables par le nombre de cas possibles.
– ex. Probabilité d'obtenir un nombre pair au lancement du dé:
      nombre de cas possibles 6 qui sont {1, 2, 3, 4, 5, 6} et
      nombre de cas favorables (le dé donne un chiffre pair) 3 qui sont {2, 4, 6};
      ce qui permet de calculer la probabilité: P = 3 / 6 = ½.
Valeur comprise entre 0 (événement improbable) et 1 (événement certain)
– v. Probabilité. fréquence, oméga
– a. Probability

Probabilités (théorie des –): étude des événements aléatoires, notamment appliqués aux jeux: dé, loto, tiercé …
– v. Probabilité, probabilités et statistiques
– a. Probability theory: the branch of mathematics concerned with probability.

Probabiliste (théorie – des nombres)*: branche de la théorie des nombres qui utilise explicitement les probabilités.
Étude en termes de probabilités du comportement d'une fonction arithmétique sur un ensemble donné.
– ex. Combien (la probabilité) de diviseurs (la fonction) en moyenne pour les nombres entiers (l'ensemble étudié) ? C'est de l'ordre de ln(n), valeur d'autant plus précise que n est grand. Le nombre moyen de facteurs premiers est ln ln(n).
– a. Probabilistic number theory: a subfield of number theory, which explicitly uses probability to answer questions about the integers and integer-valued functions

Problème de type NP**: problèmes qui passent pour être insolubles et dont la moindre variante fait croître démesurément la complexité de résolution.
Problème P = NP: il existe des problèmes dont on connait la solution (par hasard) car facilement vérifiable, mais peut-on la démontrer ?
– v. Problème P = NP
– a. P versus NP problem

Processus*: synonyme de méthode, procédé, manière de faire étape par étape.
– v. Processus stochastique, processus stationnaire
– a. Stochastic process

Produit: résultat de la multiplication quels que soient les objets multipliés: nombres, expressions algébriques, ensemble, vecteurs, fonctions …
–ex. 12 est le produit de 4 par 3.
– v. Multiplication
– a. Multiplication

– v. Règle de trois, quatrième proportionnelle, égalité, théorème de Thalès

Produit (symbole):
Se lit: produit de n au carré pour les valeurs de n de 1 à 3.

Produit cartésien: Ensemble formé des couples de l'un avec l'autre. Comme un développement avec parenthèses.
– ex. le produit cartésien de
A = {1, 2} et B = {A, B ,C} est
A x B = {(1,A), (1,B) , (1,C) , (2,A) , (2,B) , (2,C)}.

– v. Produit cartésien, table de multiplication, vocabulaire des structures algébriques
– a. Cartesian product

Produit scalaire de deux vecteurs: le produit de leur module par le cosinus de leur angle:
Le résulta est un nombre, un scalaire.
– v. Vecteur, produit scalaire, produit scalaire et théorème de Pythagore
– a. Dot product, Cartesian product of two vectors
– note: cross product of two vectors = produit vectoriel.

Produit vectoriel de deux vecteurs: un vecteur orthogonal aux deux premiers.
Le résulta est un nombre, un vecteur.
– v. Produit vectoriel
– a. cross produt of two vectors

Produit de deux matrices: Voir Multiplication de deux matrices.

Programme: ensemble des instructions permettant de traiter un problème sur ordinateur. Synonyme de code ou encore de logiciel.
– v. Informatique, programmes, algorithmes

Programmer en informatique: créer, rédiger, coder un programme.
Un programme écrit doit être testé et débogué (corrigé, déverminé).
– syn. coder, écrire du logiciel
– v. Codage, débogage, recette, Scratch, Python, Maple, Maxima
– a. Programming, coding, writing instructions, writing a computer program; testing, debugging

Programmation (informatique)    >>> – a. Computer programming
Programmation linéaire                >>> – a. Linear programming

Programmation dynamique: méthode algorithmique pour résoudre des problèmes d'optimisation comme le problème du voyageur de commerce ou celui du sac à dos.
Il faut entendre programmation selon son sens premier: planification et ordonnancement.
La programmation dynamique consiste à résoudre un problème en le décomposant en sous-problèmes, puis à résoudre les sous-problèmes, des plus petits aux plus grands en mémorisant les résultats intermédiaires.
– v. Algorithme, logiciel, ordinateur /
       Programmation, programmes sur les pages de ce site– Index
– a. Dynamic programming

Progression: synonyme de suite

Progression arithmétique ou suite arithmétique: suite de nombres dont chacun est égal au précédent plus une constante (la raison).
La raison est la différence entre deux termes consécutifs.
– v. Suite arithmétique
– ex. 3, 8, 13, 18, 23, … la raison est 5.
– a. Arithmetic progression or arithmetic sequence

Progression arithmétique généralisée ou ensemble linéaire**: suite arithmétique dont la raison est variable.
– ex. 3, 5, 8, 10, 13, 15, 18, … addition successivement de 2 puis 3.
– a. Generalized arithmetic progression or multiple arithmetic progression

Progression géométrise, harmonique: Voir Suite géométrique …

Projection orthogonale d'un point sur une droite: c'est la plus courte distance du point à tout point de la droite. Cette projection met en jeu deux droites perpendiculaires, la droite sur laquelle on projette et la direction de projection.
– v. Projection des triangles, des polygones, perspective cavalière
– a. Orthographic projection

Pronique: autre mot pour dire oblong ou produit de deux nombres successifs comme 4 x 5 = 20.
– a. Pronic number or oblong number or heteromecic number

Proportion: synonyme de rapport, de pourcentage.
Aussi: égalité entre deux rapports.
– ex. 5 sur 20 élèves sont notés A, la proportion est 5/20 = 0,25 = 25%.
– v. fProrata, fraction, règle de trois, multiplication
– a. Proportionality, equality of two ratios

Proportionnel, inversement proportionnel: adjectifs utilisé pour témoigner d'une relation de proportion.

L'intensité de la force d'attraction entre deux objets est proportionnelle à la masse de chacun et inversement proportionnel au carré de leur éloignement. Voir loi en carré inverse ci-dessous.

Proportionnalité (coefficient de -): facteur multiplicatif constant dans un couple de suites proportionnelles.
– v. Constante de proportionnalité et coefficient de proportionnalité
– a. Coefficient of proportionality or proportionanlity constant

Divine proportion: synonyme de nombre d'or.

Proportion directe: deux variables sont dites directement proportionnelles, ou en proportionnalité directe, si leur quotient est constant.

La constante m est le coefficient de proportionnalité.
La proportion témoigne d'une relation linéaire; Sa représentation graphique est une droite.
– ex: le prix des carottes est proportionnel à son prix au kilogramme.
– a. direct proportion: two variables x and y are said to be in direct proportion when y = k٠m, for a constant m.

Proportion inverse (inversement proportionnel): proportionnel à l'inverse du paramètre.

– ex: avec une voiture roulant à vitesse constante, la durée d'un parcours donné est inversement proportionnelle à la vitesse: T = D / V et, on dit que: T est inversement proportionnel à V.
– propriété: le produit de variables inversement proportionnelles est constant. Il est égal au coefficient de proportionnalité.
– a. inverse proportion: two quantities are said to be in inverse proportion if an increase in one leads to a decrease in the other quantity and a decrease in one leads to an increase in the other quantity

Loi en carré inverse: en physique, loi postulant qu'une quantité physique (énergie, force, ou autre) est inversement proportionnelle au carré de la distance de l'origine de cette quantité physique. Cette loi est typique d'un phénomène en propagation sphérique (acoustique, électromagnétisme, gravitation …)

Proportion double, multiple: proportions en cascade.
Une proportion (directe ou inverse) entre x et y, puis une autre proportion entre y et z qui induit une proportion double entre x et z.
– ex: le prix des carottes est proportionnel à son prix au kilogramme et, le prix au kilogramme est inversement proportionnel à la quantité récoltée (plus il y en a sur le marché, moins elles sont chères). La quantité récoltée est proportionnelle à la quantité de pluie au printemps. Etc.
– énigmes: huit ouvriers posent 8 000 carreaux en huit jours. Combien de carreaux seront posés par 4 ouvriers en quatre jours? Réponse 2 000.
– v. Énigmes avec calcul de double proportion
– appli*. retrouver les coordonnées d'un point cadastral connaissant son environnement en latitude et en longitude.
– a. double proportion

Loi des proportions définies: loi de chimie selon laquelle lorsque deux ou plusieurs corps simples s'unissent pour former un composé défini, leur combinaison s'effectue toujours selon un même rapport pondéral.

Loi des proportions multiples: en chimie, cette loi, parfois dite loi de Dalton (1803), stipule que si deux éléments forment plus d'un composé, alors les rapports des masses du deuxième élément qui se combinent avec une masse fixe du premier élément seront toujours des rapports de petits nombres entiers.
Ne pas confondre avec la loi de Dalton (1801) ou loi des pressions différentielles en thermodynamique: la pression au sein d'un mélange de gaz parfaits est égale à la somme des pressions partielles de ses constituants.
Exemple pour la loi des proportions multiples

Proposition (ou assertion): phrase déclarative qui est soit vraie soit fausse
En logique, synonyme d'énoncé, d'assertion, de théorème.
C'est une affirmation connue par tous pour être soit vraie soit fausse.
C'est un énoncé mathématique qui a une et une seule valeur : vrai ou faux.
– ex. Le soleil se lève à l'est. J'ai un chat. 2 est un nombre pair. Les trois assertions sont vraies. 3 est un nombre pair est une assertion, mais elle est fausse.
(a + b)² = a² + 2ab + b² mais (a + b)² = 100 n'est pas une proposition.
si x est un nombre réel, alors x² , mais aussi: si x est un nombre réel, alors x² . La première proposition est toujours vraie et la seconde est toujours fausse.

La négation de la proposition P est la proposition qui est vraie si et seulement si P est fausse.
Elle est notée non P ou ¬P.

– v. Logique en bref, prédicat, démonstration, théorème, axiome, hypothèses, contradiction, tiers exclu
– a. Proposition in propositional logic: declarative sentence that has a truth value.

Propositions (Calcul des -) ou calcul propositionnel: étude de la valeur de vérité des propositions liées par des opérateurs, sans tenir compte du sens de ces propositions.
– v. Logique en bref
– a. Propositional calculus

Proposition indécidable: ni validée, ni infirmée dans une théorie mathématique.
– v. Incomplétude.
– a. Undecidable problem, statements

Propre (fraction -): fraction dont le numérateur est plus petit que le dénominateur.
Elle est impropre dans le cas contraire.

Propriété: qualité particulière à quelque chose.
– ex. Dans un triangle la longueur d'un côté est toujours inférieure à la somme des longueurs des deux autres côtés: inégalité triangulaire.
– a. we will learn about the definition of an isosceles triangle and its properties.

Propriété propre ou caractéristique: une propriété qui est exclusive à l'objet décrit, qui le définit lui et lui seul.
– ex. Les animaux à six pattes sont des insectes.
– a. Specific properties, characteristics

Prorata (au -): synonyme de: dans la même proportion.
– v. Rapport, proportion, pourcentage
– v. Fraction, règle de trois, multiplication
– a. Pro rata, pro-rata, prorated, on a pro-rata basis, in proportion, proportionally

Proxy: sur Internet, serveur relais qui stocke les données en vue de faciliter leur accès.

Logiciel qui joue le rôle d'intermédiaire en se plaçant entre deux hôtes pour faciliter ou surveiller leurs échanges. Dans le cas des réseaux, un proxy est un programme servant d'intermédiaire pour accéder à un autre réseau, généralement Internet. Proxy désigne aussi le serveur qui assure les services. Mot parfois utilisé en mathématique pour imager le fonctionnement de sortes de dictionnaires d'objets, comme les groupes de Galois, facilitant ainsi leur accès.

Pseudo: soi-disant, qui passe pour, qui ressemble à.
– a. Pseudo (prononcez: su:do, sans le p)

Pseudo-aléatoire* pas vraiment aléatoire mais suffisant pour certaines applications.
– ex. Générateur de nombres pseudo-aléatoires.
– a. Pseudo-random, a pseudo-random digital sequence (une suite pseudo-aléatoire).

Puissance (fonction -) ou exponentiation: résultat de la multiplication répétée d'un nombre avec lui-même.
– On dit: a puissance n et non a exposant n.
– v. Puissance
– a. The power of a number says how many times to use the number in a multiplication.

Puissance énième: produit d'un nombre n fois par lui-même, notée aⁿ et lue a puissance n.
– ex. 7³ = 7 x 7 x 7 = 343. Se lit: sept à la puissance 3 ou sept exposant 3 (à éviter).
– a. seven to the power three.
– convention: a⁰ = 1; notez que a¹ = a;
– propriétés: aⁿ.bⁿ = (a.b)ⁿ; aⁿ.a^m = a^n+m; aⁿ / a^m = a^n-m; (aⁿ)^m = a^n.m
Le monde des puissances transforme les produits en sommes.
– ex. 8 x 32 = 2³. 2⁵ = 2³⁺⁵ = 2⁸ = 256.
– v. Puissance, calculs pratiques, exposants

– a. Power: the power (or exponent or index) is written as a small number to the right and above the base number. Also: 1 024 is the power 10 of 2 (2¹⁰ = 1 024).
– ex. 5³ could be called "5 to the third power", "5 to the power 3" or simply "5 cubed".
Exponents are also called powers or indices.

Puissance parfaite: puissance énième (n > 1) d'un nombre.
Nombre qui peut s'exprimer comme un carré ou une plus grande puissance d'un nombre
– formellement: PF = x^y avec x ≥ 1 et y >1
– cas du nombre x = 1: ce nombre, sans indication de puissance, est inclus ou non dans la liste à condition de le préciser.
– doublons, duplications: il existe une infinité de présentations telles que 9² = 3⁴ = 81.
– liste sans doublons: 1, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, …
– la somme des inverses des puissances parfaites sans doublons est égale à 1.
– v. Nombres puissants
– a. Perfect power, perfect square, perfect cube, perfect kth power

Puissance fractionnaire: autre façon d'exprimer une racine.
– ex. 100^1/2 = Ö100 = 10.
– Calcul:

– a. Power with rational exponents

Puissance négative: autre façon de supprimer les dénominateurs.
– ex. 10^-2 = 1/10²
– v. Puissance avec exposant négatif, équations aux dimensions
– a. Negative exponent

Puissances de dix: 10^k : un "1" suivi de k zéros.
– ex. 10³ = 1000
– v. Puissances de dix et leur nom, nombre 10
– a. Power of 10

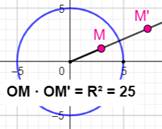
Puissance de l'inversion* nombre réel k, pris comme constante du produit de deux distances.
– ex. Sur l'illustration le point M' est l'image du point M par inversion de centre O et de puissance 25, le carré du rayon du cercle d'inversion.
– v. Inversion
– a. Circle inversion, inversive geometry

Puissance d'un ensemble**: synonyme de cardinal.
Quantité d'élément dans un ensemble, généralement infini.
Deux ensembles ont même puissance – ou ont le même nombre d'éléments – s'ils sont équipotents, c'est-à-dire s'ils sont en bijection.
– déf. L'ensemble des parties d'un ensemble, parfois appelé ensemble puissance, désigne l'ensemble des sous-ensembles de cet ensemble y compris l'ensemble lui-même et l'ensemble vide.
– a. Power set: the set of all subsets.

Puissance du dénombrable** (ensemble dénombrable): un ensemble à la puissance du dénombrable ( lire aleph zéro), s'il est équipotent à , l'ensemble des nombres entiers.
C'est la cas pour l'ensemble des nombres pairs, celui des nombres premiers, celui des nombres algébriques …
– a. Countable set: it has the same cardinality as some subset of the set of natural numbers

Puissance du continu**: un ensemble à la puissance du continu (), s'il est équipotent à , l'ensemble des nombres réels.
– ex. L'ensemble des nombres transcendants à la puissance du continu.
– a. Cardinality of the continuum is the cardinality or "size" of the set of real numbers.

Pyramide: solide dont la base est un polygone et les faces latérales sont les triangles issus d'un sommet (apex) et s'appuyant sur chacun des côtés du polygone de base.
– v. Pyramide
– a. Pyramid

Pyramide régulière: elle est régulière si le polygone de la base est régulier et si le sommet est situé sur la perpendiculaire au centre du polygone (la projection orthogonale du sommet est le centre du polygone).
– ex. Le tétraèdre est une pyramide régulière à quatre faces.
– a. Right pyramid, oblique pyramid, regular pyramid

Pyriforme (ou piriforme): en forme de poire.
– v. Ovoïde
– a. Piriform

Pythagore (théorème de -): dans un triangle rectangle a² + b² = c², c étant l'hypoténuse.
– v. Théorème de Pythagore
– a. Pythagorean Theorem
– Inde: Gougu theorem

Pythagore (triplet de -) ou triplet pythagoricien: Trois nombres entiers dont le carré de l'un est égal à la somme des carrés des deux autres.
– ex. 3² + 4² = 5²; 5² + 12² = 13² ; 7² + 24² = 25²
– v. Triplets de Pythagore
– a. A Pythagorean triple consists of three positive integers a, b, and c, such that a² + b² = c².

Python: outil de programmation devenu universel et utilisé en lycées.
Python est un logiciel gratuit, simple dans son premier abord mais qui peut être enrichi de nombreux modules pour les plus exigeants.
Si débutant, il est conseillé de se familiariser avec Scratch.

>>> Q

Voir	Atlas des maths – des références Débutants – pour juniors ou novices
Aussi	DicoNombre – tous les nombres de 0 à l'infini DicoLettre – signification des lettres en maths et ailleurs DicoCulture lettre P
Autres	Voir page des liens et références
Cette page	http://villemin.gerard.free.fr/Referenc/Encyclop/P.htm