Dictionnaire de base du vocabulaire des mathématiques B

Balance: en comptabilité, un état (document revu régulièrement) mettant en regard ce que l'entreprise dépense (soldes débiteurs) et ce que l'entreprise perçoit (soldes créditeurs)
– v. Bilan

Banach (espace de -)**: on dit qu'un espace métrique (X,d) est complet si toute suite de Cauchy de X est convergente. Un espace vectoriel normé qui est complet s'appelle espace de Banach.
– ex. tout espace vectoriel de dimension finie sur ℝ ou ℂ, muni de n'importe quelle norme est de Banach,

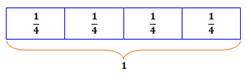Barre de fraction: représentation d'une fraction par une bande rectangulaire divisée également selon la fraction à représenter.
Utile pour l'apprentissage
– v. Méthode Singapour

Barre de fraction: ligne horizontale séparant le numérateur du dénominateur d'une fraction. Représenté en linéaire par un barre oblique.
– v. Vinculum, symboles particuliers
– a. Fraction bar, vinculum: the line that separates the numerator and the denominator in a fraction.

Barycentre: centre d'une figure géométrique dont chaque sommet est doté d'une pondération.
Point d'équilibre entre divers points dont chacun à une masse propre.
Centre de distribution des charges ou des mases d'un objet.
Si toutes les masses sont égales, on parle d'isobarycentre.
– ex. L’isobarycentre de trois points est le point de concours des médianes du triangle dont les sommets sont ces trois points. C'est le centre de gravité.
– syn. Centre d'inertie, centre de gravité, de centre de masse
– étym. Du grec barus, lourd; baros, idée de gravité ou de pression atmosphérique.
– v. Barycentre, pondération, isobarycentre
– a. Barycenter

Coordonnées barycentriques**: triplet de coordonnées dans un triangle
– v. Système de coordonnées barycentriques
– a. Barycentric coordinate system

Base de données: ensemble des données stockées sur l'ordinateur.
Ensemble d'informations structurées accessibles au moyen d'un logiciel.
– ex. liste des communes françaises avec population, superficie, nom du maire, etc.
– a. database, database management system (DBMS)

Banque de données: plusieurs bases de données regroupées.
– a. databank, a large shared data bank

Base de numération: la base décimale (base 10) est notre manière de compter par puissances de dix.
– ex. 1234 veut dire 1 x 1000 + 2 x 100 + 3 x 10 + 4;
on peut aussi compter par 8 (octal) ou par 2 (binaire) …
La base est la quantité de chiffres du système de numération.
– v. Base de numération
– a. Radix or base: the number of unique digits, including the digit zero, used to represent numbers

Base des logarithmes* : le logarithme de base b d'un nombre réel strictement positif est la puissance à laquelle il faut élever la base b pour obtenir ce nombre.
– ex. log (10 000) en base 10 = 4 car 10⁴ = 10 000.
– notation: log₁₀ (10 000) = 4; ln(a) indique que la base est la constante e.
– v. Logarithme
– v. Logarithme: the logarithm base 10 of 10 000 is 4.

Base d'une élévation à une puissance ou base d'exponentiation: le nombre élevé à la puissance.
– ex. 2¹⁰ = 1 024, le nombre 2 est la base et le nombre 10 l'exposant.
– v. Puissance
– a. Base: the power is written as a small number to the right and above the base number

Base ou repère: Voir Repère

Base d'un espace vectoriel*: son système d'axes; la base est définie par une série de vecteurs non colinéaires; ex: pour le plan, la base du plan vectoriel sera définie par un couple de vecteurs ; une base munie de la même origine est appelée repère; et avec des vecteurs orthogonaux et de norme unitaire, le repère est orthonormé.
– v. Base et repère
Vector space, base

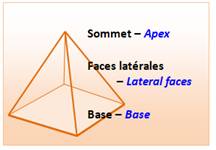
Base d'une figure géométrique
En 2D, c'est un côté particulier d'un polygone;
– ex: la base du triangle isocèle, la base du trapèze;
En 3D, c'est la figure plane qui permet de créer certains solides (cône, prisme, pyramide); côté opposé au sommet (apex); ex: la base du cône est un cercle, la base d'une pyramide régulière est un polygone.
Les autres faces que la base sont les faces latérales.

Base (d'une topologie): ensemble d'ouverts, chacun réunion d'éléments de cet ensemble.
Ainsi les propriétés d'une de ses bases s'appliquent à la topologie complète. Une base caractérise une topologie.
– a. Base or basis

Base (angle à la -): dans un triangle isocèle, chacun des angles formés par un des côtés et la base d'u triangle isocèle, par exemple; ils sont égaux.
– v. Angles à la base
– a. The angles that involve the base of an isosceles triangle are known as the base angles.

Base 100 (indice -): comparaison de l'évolution de valeurs en supposant que l'un d'entre eux vaut 100.
– ex. le prix d'un paquet de café selon les années en donnant une valeur 100 en 2005, par exemple.
– v. Indice, règle de trois, quatrième proportionnelle, nombre 100
– a. Index base 100

Beauté: relation, identité ou formule considérée comme encapsulant un résultat simple pour une réalité apparente complexe.
– v. Pépites, appréciation de Dirac
– quelques exemples:

La relation d'Euler est un parfait exemple de beauté mathématique dont Euler disait qu'elle révélait la présence de la main de Dieu;

Les images de fractales sont une source de ravissement sans fin;

Les démonstrations muettes; etc.

Beauté mathématique: plaisir esthétique émanant de travaux mathématiques. Mathématiques vues comme une création artistique au même titre que la poésie ou la musique. Carl Friedriech Gauss (1777 -1855) hésitait entre les humanités et les mathématiques. Il a alors trouvé la construction du polygone à 17 côtés et c’était tellement beau qu’il a continué dans la voie mathématique.

Bernoulli (lois de -): loi de probabilité d'une variable aléatoire discrète qui vaut 1 avec la probabilité p et 0 avec la probabilité q = 1 – p.
Bilan d'une épreuve qui n'admet que deux issues (épreuve de Bernoulli).
– v. Loi de Bernoulli
– a. Bernoulli distribution

Bernstein (polynômes de -)**: polynômes servant de base à la construction des courbes de Bézier.
– a. Bernstein polynomial

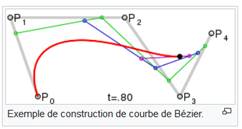Bézier (courbe de -)* courbe élémentaire utilisée en conception assistée par ordinateur (CAO).
– histo. invention commune de Paul de Casteljau en 1959 (Citroën) et de Pierre Bézier en 1962 (Renault).
– ex. Voir cette illustration avec animation en: Courbe de Bézier
– a. Bézier curve

Bézout (identité de -) ou théorèmes de Bachet-Bézout: deux nombres entiers a et b sont premiers entre eux ssi on peut trouver deux entiers relatifs tels que .
Connu aussi en tant que relation de Bézout, ou encore, identité de Bachet.
– v. Identité de Bézout
– a. Bézout's identity or Bézout's lemma

Bicarré: synonyme de puissance quatrième.
– ex. 0, 1, 16, 81, 256, 625, 1296, 2401, 4096, …
– v. Bicarré
– a. Biquadrates number or tesseractic numbers

Bicarrée (polynôme ou équation -): de la forme
– v. Équations
– a. polynomials with higher powers than squre and cube are called quartic, quintic, sextic, heptic, and octic before they stop having names.

Bijection: correspondance un pour un dans les deux sens.
Application à la fois injective et surjective.
Deux ensembles en bijection sont appariés.
– autres noms: Fonction bijective, application bijective
– ex. Un humain et son numéro de sécurité sociale.
– ex. Les fonctions exponentielle et logarithme sont deux fonctions bijectives réciproques.
– relation: bijection = injection + surjection
– v. Bijection, vocabulaire des structures algébriques
– a. Bijection, one-to-one correspondance or mapping, bijective function

Une bijection est une application (ou fonction) où, dans un ensemble d'arrivée, tous les éléments ont un élément et un seul dans l'ensemble de départ et où le nombre d'éléments de l'ensemble d'arrivée est égal au nombre d'éléments de l'ensemble de départ.
Chaque point M de E a une image P en F, et une seule et unique; les éléments de E et leur image en F se correspondent un à un.

Bilan: état comptable d'une entreprise montrant sur deux colonnes, d'un côté, comment se finance l'entreprise (passif) et, de l'autre, comment elle utilise ses fonds pour développer son activité (actif). La somme de l'actif est comparée à celle du passif. La différence témoigne des bénéfices ou des pertes de l'entreprise. Ce constat est porté dans le bilan pour équilibrer (balancer, rendre égal) le montant de l'actif et celui du passif.
– a. Balance sheet

Bilinéaire (application -)**: c'est une application analogue à une application linéaire, mais à deux variables.
Une application bilinéaire est une fonction combinant des éléments de deux espaces vectoriels pour donner un élément d'un troisième espace vectoriel, et elle est linéaire dans chacun de ses arguments.
– ex. multiplication matricielle
– a. bilinear map

Il nous faut donc trois espaces vectoriels sur K : E, F et G.
Et l’application f : E × F → G .
Elle est bilinéaire si les égalités suivantes sont vérifiées pour toutes les valeurs de :

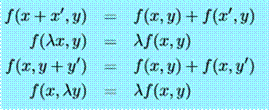
Billiard: 1000 billions = 10¹⁵

Billion: billion = 10¹² = 1000 milliards; – v. Billion, zillion, noms des grands et des petits nombres
– attention: billion_{US, CANADA} = 10⁹ = milliard_FRANCE

Bimédiane: dans un quadrilatère convexe, segments qui joignent les milieux des côtés opposés.
– a. Bimedians: the two bimedians of a convex quadrilateral are the line segments that connect the midpoints of opposite sides.

Binaire: manière de compter par 2, comme les ordinateurs avec 0 et 1
– v. Binaire, numération, décimale.
– a. Binary number: number expressed in the base-2 numeral system or binary numeral system

Opérateur binaire: qui comporte deux opérandes.
– ex. Les quatre opérations classiques sont des opérateurs binaires.
– v. opérateur unaire

Binaire (relation -): se dit d'une relation d'un ensemble sur lui-même.
Relation de E vers E;
– ex. l'addition est une relation (opération) binaire.
– v. Relation binaire
– a. A binary relation associates elements of one set, called the domain, with elements of another set, called the codomain

Prédicat binaire: un prédicat qui établit une relation entre une paire d'objets.
Un prédicat n-aire exprime une relation entre n objets.
– a. binary predicate; 2-ary predicate

Binôme: polynôme à deux termes.
Quand la somme de deux monômes n’est pas un monôme, c’est un binôme.
– ex. si a, b, x, y sont des nombres réels : ax + 2 ab = 3 ax est un monôme;
a + b, a² + 6b³ax + b, a²x³ + by, ax² – by

– v. Polynôme, trinôme, monôme;

Nom qui apparaît 1554. On le retrouve en adjectif en 1613. Il signifie: composé de deux parties. Il viendrait du latin binomium, de bis et de nomem, quantité algébrique à deux termes. En 1842, ce terme désigne aussi à des étudiants qui travaillent ensemble.

Binôme de Newton: développement d'un binôme élevé à une puissance (a + b)ⁿ .
– ex. (a+b)² = a² + 2ab + b²; (a+b)³ = a³ + 3a²b + 3ab² + b³ .
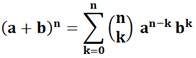Les coefficients sont les nombres du triangle de Pascal: 1 2 1 puis 1 3 3 1, etc.
D'une manière générale, on a cette formule:

Lecture de la formule: le développement du binôme (a + b) à la puissance n est égal à la somme des termes de 0 à n, chacun étant le produit d'un coefficient binomial par a avec une puissance décroissante à partir de n, et b avec une puissance croissante à partir de 0.

– v. Binôme de Newton
– a. Binomial theorem

Binomial (coefficient -): coefficient du développement du binôme de Newton.
Ce coefficient donne la quantité de combinaisons de p éléments parmi q (comme au Loto).
– notation:
C'est le nombre de combinaisons de n objets pris p à p.
– v. Coefficients du binôme
– a. Binomial coefficient

Binomiale (loi -): loi discrète qui compte le nombre de succès d'une suite d'événements.
Elle modélise la fréquence du nombre de succès obtenus lors de la répétition de plusieurs expériences aléatoires identiques et indépendantes.
Répétition de n épreuves de Bernoulli identiques et indépendantes.
– v. Loi binomiale
– a. Binomial distribution

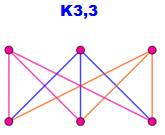Biparti (graphe -): graphe comprenant deux séries de sommets. Il est complet si chacun des sommets de l'un rejoint tous les sommets de l'autre.
– ex. Le graphe K3,3 est un graphe biparti complet.
– v. Graphe et son vocabulaire
– a. Bipartite graph or bigraph

Bipoint: couple de points dans un ordre précis. Le premier point est l'origine.
Deux bipoints (A, B) et (C, D) sont dits équipollents lorsque les segments [AD] et [BC] ont le même milieu. Les points A, B, C et D sont alors les sommets d'un parallélogramme.
– notation (A, B).
– v. Segment, vecteur, mesure algébrique
– a. Vector

Bipoints équipollents: deux bipoints (A, B) et (C, D) sont équipollents si les segments AD et BC ont même milieu.
Les segments AB et CD sont parallèles et de même mesure.
Le quadrilatère ABDC est alors un parallélogramme.
– a. Equipollent bipoints

Bipyramide ou diamant: deux pyramides régulières isométriques (les mêmes) réunies par leur base.
– a. Bypiramid: polyhedron formed by joining two congruent regular pyramids base-to-base.

Bit : Binary Digit. Élément d'information élémentaire dans un ordinateur à deux valeurs 0 ou 1 . Ne pas confondre avec byte, mot anglais qui signifie octet.
– v. Bit, informatique
– a. Bit: A binary digit, generally represented as a 1 or 0.
The smallest unit of storage in a digital computer.

Qubit ou qbit: état quantique qui représente la plus petite unité de stockage d'information quantique.
– v. Ordinateur quantique, qubit
– a. Qbit, qubit: a quantum bit.

Bitmaps: mode de définition d'une image point à point (pixel par pixel). Le fichier d'une image est volumineux comparé à une définition vectorielle.

Birapport de quatre nombres*: nombre avec sa notation:

aussi nommé rapport anharmonique.
– v. Homologie
– a. Cross-ratio or double ratio or anharmonic ratio

On parle de:

Birapport de quatre points situés sur un axe;

Birapport de quatre droites concourantes;

Birapport de quatre points sur un cercle ou une conique.

Bissectrice d'un angle: demi-droite issue du sommet de l'angle et qui le partage en deux parties égales; notez qu'il en existe deux pour chaque angle; la bissectrice d'un angle est son axe de symétrie.
– v. Bissectrice
– a. Angle bisector: it divides the angle into two angles with equal measures

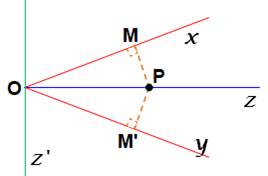Bissectrice d’un angle géométrique: on appelle bissectrice de l’angle géométrique xOy toute droite Oz qui partage l’angle xOy en deux angles égaux. Il existe deux telles droites Oz et Oz’, qui sont perpendiculaires ; Oz est appelée bissectrice intérieure, Oz’ bissectrice extérieure (imaginez que Ox et Oy sont prolongés).
La bissectrice de l'angle xOy est l'unique demi-droite Oz telle que la symétrie orthogonale par rapport à Oz échange les deux demi-droites [Ox) et [Oy).
La bissectrice de l'angle xOy est aussi l'ensemble des points qui sont à égale distance des demi-droites [OA) et [OB): PM = PM'.
La bissectrice extérieure de l'angle xOy est la droite perpendiculaire à Oz passant par O. Si P est le symétrique de M par rapport à O, la bissectrice extérieure de MOM' est la bissectrice de MOP.
Bissectrices d'une paire de droites sécantes: les deux bissectrices vues prcédemment.

Bissectrices d’un triangle: les bissectrices des trois angles d’un triangle ABC sont appelées bissectrices du triangle. Les trois bissectrices intérieures sont concourantes en un point I qui est le centre du cercle inscrit dans le triangle.

Biunivoque: Qui fait correspondre un à un, les éléments de deux ensembles.
– ex. La droite numérique réalise une correspondance biunivoque entre l'ensemble des nombres réels et les graduations et sous-graduations de la droite.
– v. Bijection
– a. one-to-one

Bloc de trois chiffres: la norme SI précise que, pour la lisibilité des nombres, leurs chiffres peuvent être groupés par blocs de trois séparé par un espace. Le virgule (ou le point) est le séparateur décimal.
– ex. 1 000 000 ; 1 000 000, 234 567 89
– v. Bloc de trois chiffres
– a. Cipher. Ex. 1,000,000 is a number having two ciphers of zeros

Boole (algèbre de-) ou calcul booléen: arithmétique particulière utile en logique.
– v. Algèbre de Boole
– a. Boolean algebra

Booléen (variable): qui prend la valeur 0 ou 1 exclusivement.
– v. Fonction booléenne
– a. Boolean value

Bon ordre: l’ensemble des entiers naturels ℕ est muni d’une relation d’ordre, notée : ≤ (inférieur ou égal à ...). L’entier a est inférieur ou égal à l’entier b s’il existe un entier c tel que a soit égal à b + c.
N’importe quelle partie A de ℕ admet un élément qui est plus petit que tous les éléments de A: Si A = { 3, 4, 5, 6 , . . . , n}, le plus petit élément de A est 3.

L’ensemble des nombres réels ℝ est aussi muni d’une relation d’ordre, notée aussi ≤ (le réel x est inférieur ou égal au réel y si la différence y - x est positive).

Une partie de ℝ constituée par un intervalle fermé [a, b] ou un intervalle semi-ouvert [a, b[ ou [a, +ꝏ[ admet bien un plus petit élément : a. Mais ce n'est pas le cas pour une partie ouverte ]a, b[ (car, si on considère un nombre x quelconque de ]a, b[ aussi proche soit-il de a, il existe toujours un nombre réel y qui est compris entre a et x, donc qui soit inférieur à x.

On dit que ℕ est bien ordonné, ou encore que la relation d’ordre de ℕ est une relation de bon ordre, tandis que la relation d’ordre de ℝ n’est pas une relation de bon ordre.
De façon générale, une relation d’ordre dans un ensemble E est une relation de bon ordre si toute partie non vide de E admet un plus petit élément.

Borne: la plus grande des valeurs (supérieure) ou la plus petite (inférieure) d'un intervalle.
Un intervalle est un ensemble ordonné de points compris entre deux bornes.
– a. Endpoints: An open interval does not include its endpoints, and is indicated with parentheses.

Partie bornée: une partie A de est bornée si elle est majorée par M et minorée par N. La borne M est telle que, pour tout x de A, x M; La borne N est telle que, pour tout x de A, x N.
Cette notion de majorant, minorant et borné s'étend aux fonctions: f(x) M; f(x) N.
– a. Bounded set

Ensemble borné: dans l’ensemble ℕ des entiers positifs, on a défini une relation est inférieur ou égal à . Si on considère le sous-ensemble de N constitué des trois nombres 3, 4, 5 : A = { 3, 4, 5 }, tous les éléments de A sont inférieurs ou égaux à 5 et ils sont tous supérieurs ou égaux à 3 ; la partie A de ℕ est bornée.
L'ensemble ℕ n’est pas borné, car on ne peut trouver un entier p tel que tous les autres lui soient inférieurs.
Soit E un ensemble sur lequel est définie une relation d’ordre (notée ≤) ; une partie de A est dite bornée s’il existe deux éléments m et M de E tels que tout élément x de A soit à la fois inférieur ou égal à M et supérieur ou égal à m :
Tout intervalle fini de ℝ (ensemble des nombres réels) est borné.

Application bornée: une application f d’un ensemble E vers un ensemble F muni d’une relation d’ordre est dite bornée si l’image par f de E est une partie bornée de F.
Par exemple, l’application f de l’intervalle [0, 1] dans R qui à tout nombre réel x de [0, 1] fait correspondre le nombre réel f(x) = 2x + 1 est bornée, car si x est compris entre 0 et 1, alors f(x), par exemple 2x + 1, est compris entre 1 et 3.

Boule: volume compris dans la sphère; parfois nommée sphère si pas de confusion possible; la boule de centre O et de rayon r est l'ensemble des points M de l'espace tels que .
– v. Sphère
– a. Sphère

Soient E un ensemble muni d’une distance d, x un point de E et r un nombre réel positif. On appelle boule ouverte de centre x et de rayon r et on note B(x, r) l’ensemble des éléments y de E dont la distance à x, d(x, y), est strictement inférieure à r. On note:

On appelle boule fermée de centre x et de rayon r l’ensemble des éléments y de E dont la distance d(x, y) a x est inférieure ou égale à r. On la note:

Boustrophédon (transformation -)**: sorte de transformation en zigzag. Tient son nom de l'écriture ancienne en boustrophédon qui allait de gauche à droite puis continuait de droite à gauche, ainsi de suite.

Nombres boustrophédon: Suite de nombres issues des diverses permutations alternées d'un jeu de nombres. Ex: U₄ = 5 car les permutations alternées sont: (1324), (1423), (2314), (2413) et (3412). Ces nombres sont liées aux nombres d'Euler et ceux de Bernoulli.
– v. Nombres zigs et zags
– a. Boustrophedon

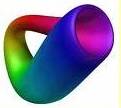
Bouteille de Klein*
– v. Klein
– a. Klein bottle

BPP**: bounded probabilistic polynomial. Calcul qui peut être exécuté en temps polynomial par une machine de Turing probabilistique.
BQP**: bounded quantique polynomial. Par une machine de Turing quantique.

Brachistochrone (courbe -): courbe dans un plan vertical sur laquelle un point matériel pesant placé dans un champ de pesanteur uniforme, glissant sans frottement et sans vitesse initiale, présente un temps de parcours minimal parmi toutes les courbes joignant deux points fixés.
– v. Gravitation
– a. Brachistochrone: curve of fastest descent,

Branche ou arête d'un graphe: chaque ligne qui joint deux sommets dans un graphe.
– v. sommet, vocabulaire des graphes
– a. edge, link, line; vertice

Branche principale d'une fonction: partie retenue comme utile pour la suite du raisonnement.
Par exemple, la partie positive d'une racine carrée est la branche principale de la fonction x^1/2 (racine carrée avec racines positives comme négatives).
Utile pour les fonctions réciproques: logarithmes, racine, arctg …

Branche d'une discipline: synonyme de partie, de sous-ensemble
– ex. La topologie est une branche des maths
– v. Branches des mathématiques
– a. Branch of mathematics

Brisée (ligne -) ou ligne polygonale: segments reliant une suite de points.
Une ligne brisée fermée est un polygone.
– v. Ligne polygonale
– a. Polygonal chain: a connected series of line segments.

Brownien (mouvement -): mouvement erratique, aléatoire, dans tous les sens; distribution statistique selon une loi gaussienne;
Mouvement incessant de particules microscopiques en suspension dans un liquide ou dans un gaz, dû à l'agitation thermique des molécules du fluide; phénomène fut découvert en 1827 par le botaniste britannique Robert Brown; en 1905, Albert Einstein établit une description mathématique du phénomène; le nombre d'Avogadro fut évalué par le physicien français Jean-Baptiste Perrin, à partir d'une étude quantitative du mouvement brownien.
– v. Mouvement brownien, bruit gaussien
– a. Brownian motion

>>> C

Voir	Atlas des maths – des références Débutants – pour juniors ou novices
Aussi	DicoNombre – tous les nombres de 0 à l'infini DicoLettre – signification des lettres en maths et ailleurs DicoCulture lettre B
Autres	Voir page des liens et références
Cette page	http://villemin.gerard.free.fr/Referenc/Encyclop/B.htm