|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CRIBLE de la ROUE Crible de Prichard (1982) Critère
de primalité, alternative au crible d'Ératosthène. Méthode
qui s'appuie sur la connaissance des k plus petits nombres premiers et évite
l'analyse d'une grande quantité de nombres composés. |
|
|
||||||||||
|
Principe Le crible
d'Ératosthène élimine rapidement tous les nombres pairs, puis les
multiples de 3, etc. Le crible
de la roue combine ces effets en éliminant tous les nombres en progression
arithmétique derrière un nombre premier. Construction (Voir
tableau)
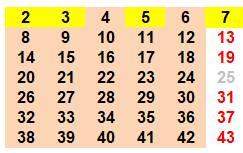
Bilan Seule la colonne 7 contient des nombres premiers. Les autres sont soit composées comme les colonnes
en 4, 5 et 6, ou alors en 2 + 6k ou 3 + 6k donc divisibles par 2 ou 3. |
Exemple avec (2, 3)
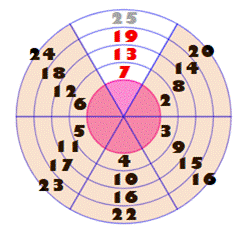
Disposition en roue
|
|||||||||
|
|
|||
|
Plus la
base compte de nombres premiers et plus le crible est efficace. |
Base: (2, 3, 5) PPCM: 30 = 2 × 3 × 5 = primorielle 5 Roue: 7, 11, 13, 17, 19, 23, 29 et 31 |
||
|
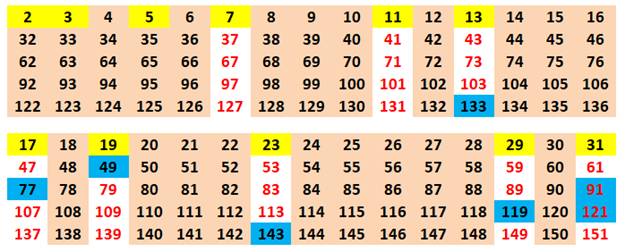
Présentation en tableau |
De nombreuses colonnes sont éliminées (ocre) Seules les colonnes des nombres premiers de la
roue sont à examiner. En rouge, les nombres premiers et en bleu, les nombres
composés. Ceux-ci sont divisibles par les premiers de la roue (ex: 133 = 7 x
19). |
||
|
Rappel |
Liste des 36 nombres premiers de 2 à 151: {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127,
131, 137, 139, 149, 151} |
||
|
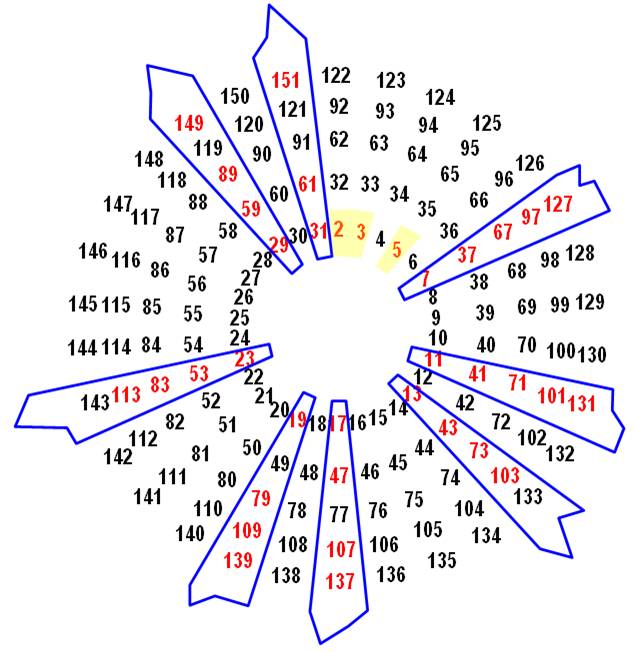
Languette bleue (ou
pétales de marguerite): zone de possibilités de nombres premiers (40 nombres
jusqu'à 151). En rouge, les nombres premiers confirmés (33
premiers + 3 de la base et 7 composés).
On se souvient que les nombres premiers se
trouvent de part et d'autre des
multiples de 6. D'où trois couples de languettes jumelles autour de 12,
18 et 30. QUASI-PREMIERS Les nombres figurants dans les languettes sont appelés quasi-premiers
de base (2, 3,5) |
|||
|
|
||
|
import
math # Test si
premier avec crible de la roue def
CR( N): T = 1; rx = int
(math.sqrt(N)) roue = [7, 11, 13, 17, 19, 23, 29, 31] if (N
< 2) : T = 0 if (N
% 2 == 0 or N % 3 == 0 or N % 5 == 0): T = 0 for i in range(0,
rx, 30) : for
r in
roue: if
(r > rx): break else
: if
(N % (r + i) == 0) : T = 0 break if T
== 0: break return
T #
Principal L = [2, 3,
5 ] for
N in range
(1, 152): if CR(N) == 1: L.append(N) print
(L) |
But Éditer la liste des nombres premiers en utilisant
le crible de la roue et la base (2, 3, 5) tout en conservant la possibilité
de chercher le primalité d'un nombre en particulier. Commentaires Définition de la fonction CR pour Crible Roue. Témoin T de
primalité: à 1 si le nombre est premier. Diviseur le plus grand possible pour en rx. Définition de la liste roue. Traitement des cas des diviseurs jusqu'à 5. Deux boucles: la première en i correspond aux couches (les couronnes dans la
roue); la seconde en r balaie les valeurs
de la roue. Arrêt (break) si
le diviseur r dépasse la valeur maximale pour n (rx). Reste de la division (mod
avec symbole: %) par la somme de la valeur
en roue r et de la composante couche en i
multiple de 30. Si reste nul, le témoin T est mis à 0 et arrêt. Si aucun cas de divisibilité n'a été rencontré le
témoin T n'a pas été modifié. Il est resté à 1. La fonction retourne al valeur de T. Le programme principal établit la liste des
nombres premiers. Les trois plus petits sont placés dans la liste à son
initialisation. Résultat [2, 2, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41,
43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127,
131, 137, 139, 149, 151] |
|
Voir Crible d'Ératosthène avec
Python
|
|
||||
|
Particularité On peut transcrire le programme Python en Maple
pour calculer la primalité d'un nombre ou d'une liste. |
Ici, la méthode utilisée consiste à utiliser la liste
des nombres premiers au fur et à mesure de leur connaissance pour tester les
divisibilités. |
|||
|
|
But Éditer la liste des nombres premiers avec le
crible de la roue et base (2, 3, 5). Commentaires L'ensemble roue
plus un ensemble accessoire où le 31 est remplacé par le 1. Boucle d'exploration de n. Diviseur le plus grand possible pour en rx. Témoin T de
primalité: à 1 si le nombre est premier. Élimination des multiples de 2, 3 et 5 (T = 0),
mais conservation de 2, 3 et 5 (T = 1). Test si n est un nombre appartenant aux
"languettes", cad. si son mod 30 est dans rou1.
Inutile de chercher pour r supérieur à racine de n (rx). Donc, on cherche parmi les nombres de la
"languette" ceux qui sont divisibles par un nombre premier déjà
trouvé. Ils sont à éliminer (T = 0). En fin d'exploration des "languettes",
si T est à 1, le nombre est premier. Il
est placé dans l'ensemble de sortie L et
aussi dans l'ensemble de référence pour les tests de divisibilité (rou1). En bleu, le résultat de ce traitement: nombres
premiers entre 1 et 200. |
|||
|
Listing pour
copier coller dans Maple |
restart; L := {}: roue := {7, 11, 13, 17, 19, 23,
29, 31}: rou1 := {1, 7, 11, 13, 17, 19, 23, 29}: for n to 200 do rx :=
round(sqrt(n)); T := 1; if n = 1 or `mod`(n, 2) = 0 or `mod`(n, 3) = 0 or
`mod`(n, 5) = 0 then T := 0 end if; if n = 2 or n = 3 or n = 5 then T := 1
end if; if member(`mod`(n, 30), rou1) then for r in roue do if r > rx then
break end if; if `mod`(n, r) = 0 then T := 0 end if end do end if; if T = 1
then L := {n, op(L)}; roue := {n, op(roue)} end if end do:L; |
|||
Voir Programmation – Index
|
L'algorithme
complet de la roue consiste à calculer les nombres premiers sur les roues des
primorielles successives : 2, 6, 30, 210, 2 310 ... Ainsi,
l'effet de l'algorithme de la roue est redoutable ! Animations pour une meilleure
compréhension >>> Vous y trouverez aussi
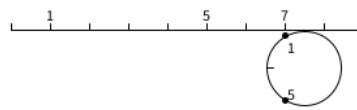
l'algorithme et le code pour programmation Effet de
la roue 2 (premier 1 et 5) Présentation roue sur
droite
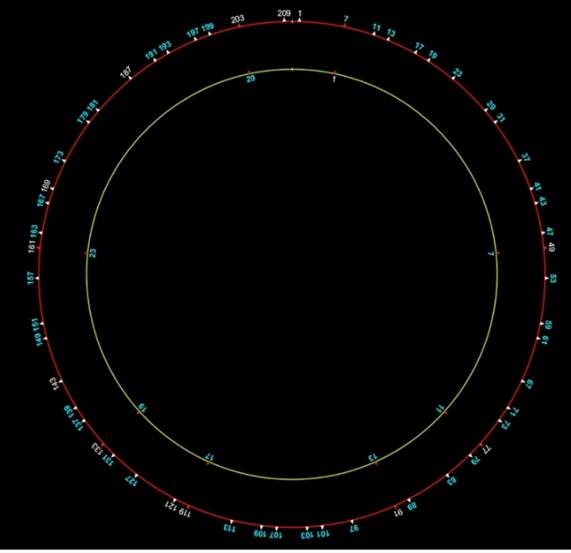
Effet de
la roue 3 (premiers 1, 7, 11, 13 17, 19, 23, 29) Présentation roue dans
roue: la petite est grossie pour se superposer à la grande. Les nombres
atteints par la petite sont supprimés. Exemple: le 11 donnera 77 qui sera
effacé.
Source des ces images:
les animations référencées |
![]()
|
Voir |
|
|
Aussi |
|
|
Sites |
|
|
|
|
|
Cette page |
![]()