NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/05/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres PREMIERS
Débutants Nombres Premiers	Généralités					Glossaire Nombres Premiers
INDEX Nombres premiers	Débutant	Introduction	Barre magique		Propriétés
	Glossaire	Caractérisation	Un		Composés
		Sommaire de cette page >>> Approche >>> En bref >>> Vue panoramique >>> Deux propriétés essentielles >>> P x P' jamais carré >>> Premiers et leurs voisins >>> Anglais		Sur pages suivantes >>> Propriétés >>> Densité >>> Records >>> Historique >>> Différence entre premiers >>> Petit théorème de Fermat >>> Démonstration d'Euclide

NOMBRES PREMIERS

Introduction

La famille: 2, 3, 5, 7, 11, 13 … >>>

Quelques propriétés fondamentales:

Seul le nombre 2 est un nombre premier PAIR >>>

Seuls {3, 5, 7} forme un triplet de nombre premiers consécutifs impairs >>>

Il n'existe pas de formule algébrique pour atteindre un nombre premier >>>

Il existe une infinité de nombres premiers >>>

Il existe des espaces aussi grands que l'on veut entre deux nombres premiers >>>

La factorisation d'un nombre en facteurs premiers est unique >>>

La signature d'un nombre premier est [1] >>>

Il y autant de nombres premiers dont la somme des chiffres est paire ou impaire >>>

Quelques problèmes ouverts:

On ne sait pas si les premiers jumeaux sont en quantité infinie >>>

On ne sait pas s'il existe une infinité de nombres premiers ne comportant pas le chiffre 7.

Suite en Propriétés

La reconnaissance des nombres premiers et des nombres composés avec leur décomposition en facteurs premiers est connue pour être des plus importants et utiles en arithmétique.

Il a tant impliqué le zèle et la sagesse des géomètres anciens comme modernes qu'il serait superflu d'en discuter plus avant...

En plus, la dignité des sciences mêmes semble exiger que tous les moyens possibles soient explorés pour trouver la solution d'un problème si élégant et si célébré.

Karl Friedrich Gauss,

Disquisitiones Arithmeticae, 1801

Voir Pensées & humour

APPROCHE
Il y deux manières principales pour marier les nombres:
l'addition	et la multiplication
Pour un entier donné:
On peut toujours trouver une somme d'entiers plus petits, jusqu'à obtenir une somme de 1. On peut toujours obtenir une partition d'un nombre. 12 = 6 + 6 = 3 + 2 + 5 + 1 = … 13 = 6 + 7 = 4 + 2 + 1 + 6 = …	MAIS, on ne peut pas toujours trouver un produit d'entiers plus petits. Ces nombres sans produit se singularisent: ce sont les nombres premiers. 12 = 3 x 4 13 = impossible !

Voir Nombres premiers imagés / Addition / Multiplication

En bref
Tout nombre n est divisible par un et par lui-même n. Ces deux diviseurs (1 et n) sont dits triviaux (synonyme de "évidents"). Un nombre qui a d'autres diviseurs que ceux-là est un nombre composé. Un nombre qui n'a pas d'autres diviseurs que ces deux triviaux est un nombre premier. Et que dire de 1 ? Il est spécial: Ni premier, Ni composé.	11 est divisible par 1 et par 11. 1001 est divisible par 1 et par 1001. n est divisible par 1 et par n. 28 est divisible par 1, 2, 4, 7, 14 et 28. 28 a 6 diviseurs dont 4 non triviaux. 28 est composé. 29 est divisible par 1 et 29 et rien d'autre. 29 est un nombre premier. 1 est divisible par 1 et par lui-même 1. Oups! C'est deux fois la même chose. On convient que 1 est spécial.
Remarque sur la définition Lorsqu'on compte les facteurs d'un nombre (les diviseurs premiers), on y inclut le 1 et le nombre lui-même. Ainsi, les diviseurs de 10 sont {1, 2, 5, 10}; ils sont quatre. Les diviseurs de 11 sont {1 et 11}; ils sont deux. Soit, la définition d'un nombre premier: un nombre qui n'a que deux diviseurs. Un nombre premier est donc un nombre qui a ces deux diviseurs {1 et lui-même}. À ce titre, il est comme tous les nombres, mais contrairement à tous les nombres, il n'en a pas d'autres. On dit abusivement (populaire): nombre qui est divisible par 1 et par lui-même au lieu de dire plus correctement: nombre qui possède seulement deux diviseurs distincts* 1 et lui-même. Tout simplement parce qu'il faut avoir introduit la notion de diviseur pour pouvoir formuler cette définition. * Distinct permet d'exclure le nombre 1 de la définition.

Devinette

Prenez deux nombres premiers consécutifs et faites la moyenne des deux. Est-ce que ce nombre peut être un nombre premier? La réponse est non, mais dis pourquoi?

Solution

VUE PANORAMIQUE sur les PREMIERS
Définition Un nombre entier plus grand que UN est un nombre premier si ses seuls diviseurs sont 1 et lui-même.	Exemples 10 = 2 x 5 n'est pas premier. 11 = 1 x 11 est premier. Cas du chiffre 1 Il n'est pas premier, par définition. Le début de la liste 2, 3, 5, 7, 11, 13 …

Les 25 nombres premiers jusqu'à 100

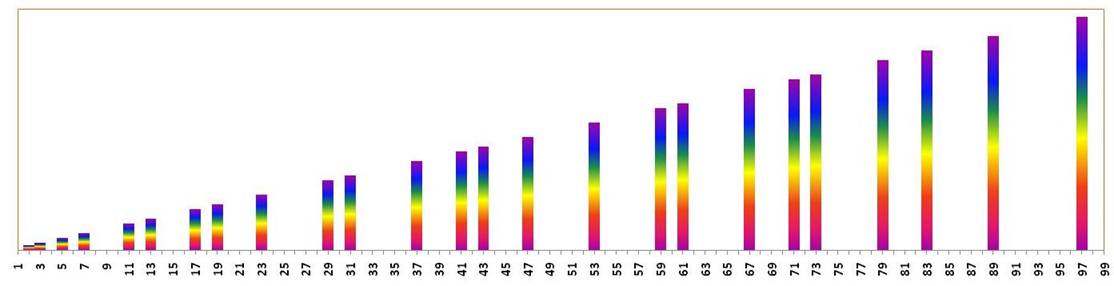
Voir Barre magique des premiers / Suite >>>

Décompte en 13

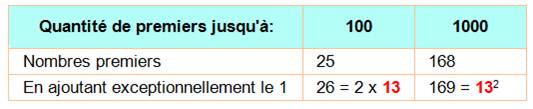
Une mystérieuse apparition du nombre 13 …

Voir Palindrome retard à 13 itérations

Merci à David H.

Théorème fondamental Tout nombre entier est représentable de manière unique comme produit de puissances de nombres premiers.

Jeu de construction Le théorème fondamental de l'arithmétique dit que les nombres premiers sont les briques de construction des nombres entiers. Exemple 2 200 = 2^3 x 5² x 11

Quantité Il existe une infinité de nombres premiers.

Espace entre deux premiers Les Grecs anciens prouvèrent (Euclide) qu'il y a une infinité de nombres premiers et qu'ils sont espacés irrégulièrement. L'espace entre deux nombres premiers est arbitraire.

Densité La quantité de premiers inférieurs ou égal à n est voisin de n/(log n) quand n devient très grand. La densité des nombres premiers est nulle.

Valeur On déduit de cette propriété qu'une valeur approchée du nième premier serait n log n. Raréfaction Les nombres premiers se raréfient pour les nombres de plus en plus grands. Voir Densité

Test de primalité – Petits nombres Pour les petits nombres, on utilise le crible d'Ératosthène. Voir Crible Voir Test de primalité

Limite La recherche consiste a supprimer tous les nombres divisibles par 2, puis par 3, puis par 5, puis par le nombre premier suivant le plus petit, etc. Elle devient vite fastidieuse, même si les ordinateurs permettent une automatisation.

Test de primalité – Grands nombres La plupart des grands nombres premiers sont recherchés en utilisant des cas particuliers du théorème de Lagrange concernant la théorie des groupes. Voir Groupe Voir Grands nombres Le théorème de Lagrange fait appel a des notions avancées. Il précise que le cardinal d'un sous-groupe divise le cardinal du groupe.

Bref Historique En 1984, Samuel Yates définit les nombres premiers de plus de 1 000 chiffres comme titaniques. Il y en avait 110 à cette époque; on en connaît plus de 1 000 fois plus aujourd'hui. Avec la puissance des calculateurs et la recherche en cryptographie, ce nombre continue à croître. On connaît des mégapremiers depuis 1999. La liste des 6 000 plus grands nombres premiers est disponible sur Internet.

DEUX PROPRIÉTÉS ESSENTIELLES
Irrégularité des premiers Il n'y a pas de formule donnant la répartition exacte. Parfois, ils sont très proches, comme les nombres premiers jumeaux. Il y a une infinité de jumeaux (conjecture) Et pourtant, il est toujours possible de trouver une paire de premiers avec un écart aussi grand que l'on veut. On peut même imaginer un écart infini entre deux nombres premiers.	Les quatre nombres premiers 821 823 827 829 forment un quadruplet, avec un écart de 8 entre chacun. Soit la moyenne de l'écart: 8 / 3 = 2,66. Les quatre nombres premiers 773 787 797 809 forment une séquence de 4 premiers. L'écart est 36. La moyenne de l'écart est 36 / 3 = 12. L'écart se creuse lorsque les nombres deviennent de plus en plus grands.

Évanouissement des premiers Il existe une formule donnant la répartition approximative des nombres premiers. Et pourtant, ils sont de moins en moins nombreux lorsque les nombres sont grands. Se pourrait-il: Qu'ils disparaissent pour de très, très grands nombres? Qu'il n'y en ait plus du tout à partir d'une certaine limite ? Non! Car les premiers sont nombreux: Il y a une infinité de nombres premiers. Même s'ils sont de plus en plus rares, il en existe toujours, même pour de très, très grands nombres? On connaît même l'écart moyen entre ces nombres premiers même très grand En 1792, Gauss très jeune remarque que les premiers sont répartis selon une loi logarithmique C'est le théorème fondamental des nombres premiers (Prime Number Theorem).

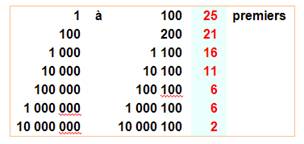
Quantité de premiers par tranche Quantification Pour un nombre n la fréquence des premiers est d'environ 1 / ln n n = 10^12 ln n = 27,63… Autour de ce nombre n, il y a en moyenne 1 nombre sur 28 qui est premier. n = 10^15 ln n = 34,53… Autour de ce nombre n, il y a en moyenne 1 nombre sur 34 qui est premier. n = 10^100 ln n = 230,25... Autour de ce nombre n, il y a en moyenne 1 nombre sur 230 qui est premier.

P x P' jamais carré
Soit N produit de deux premiers distincts	N = P x P'
Seuls diviseurs de N:	{P, P' et N}
Si est un carré:	N = C x C
Alors C est un diviseur de N. Il est égal à P ou P'. Pas à N, bien sûr.	C= { P, P'}
Disons: C = P.	N = C x C = C x P'
Conclusion impossible car P et P' sont distincts.	C = P = P'?
Plus simplement: un carré est le produit de deux nombres identiques et, le produit de deux premiers distincts ne peut pas être factorisé en un produit de deux nombres égaux.

Voir Autres propriétés

NOMBRES PREMIERS et leurs voisins

NOMBRE PREMIER	NOMBRE COMPOSÉ
Définition Nombre qui a pour seuls diviseurs un et lui-même. Exemples 2, 3, 5, 7, 11, 13 ... Particularité Tout nombre premier en 4n + 1 est somme unique de deux carrés. Voir séquences de premiers	Définition Nombre qui n'est pas premier. Il est le produit unique de facteurs premiers: " théorème fondamental de l'arithmétique ". Exemples 4, 6, 8, 9, 10, 12 … Particularité Tous les nombres sont la somme de quatre carrés au plus. Voir nombres et leurs diviseurs Voir Nombres composés

NOMBRES PARFAITS	NOMBRES AMIABLES
Définition Un nombre parfait est égal à la somme de ses facteurs premiers. Exemples 6 = 1 x 2 x 3 = 1 + 2 + 3 Voir nombres parfaits	Définition Dans une paire de nombres amiables, l'un est égal à la somme des facteurs premiers de l'autre Exemples 220 et 284 Voir nombres amiables

NOMBRES de FERMAT	NOMBRES de MERSENNE
Les nombres de Fermat: Fn = 2^n + 1 avec n = 2^x ne sont pas tous premiers	Les nombres de Mersenne: Mn = 2^n – 1 ne sont pas tous premiers

Premiers avec des premiers

Nombres de Smarandache-Wellin: nombres premiers, concaténation des plus petits nombres premiers à la suite:

2, 23, 235, 2357, 235711, 23571113, 2357111317, 235711131719, 23571113171923, 2357111317192329, 235711131719232931, 23571113171923293137, 2357111317192329313741, 235711131719232931374143, 23571113171923293137414347

Voir Propriétés

Nombres premiers concaténation de deux nombres premiers successifs:

23, 3137, 8389, 151157, 157163, 167173, 199211, 233239, 251257, 257263, 263269, 271277, 331337, 353359, 373379, 433439, 467479, 509521, 523541, 541547

Premiers avec des CHIFFRES premiers (prime-digit prime)

Chacun des chiffres est premier

2, 3, 5, 7, 23, 37, 53, 73, 223, 227, 233, 257, 277, 337, 353, 373, 523, 557, 577, 727, 733, 757, 773, 2237, 2273, 2333, 2357, 2377, 2557, 2753, 2777, 3253, 3257, 3323, 3373, 3527, 3533, 3557, 3727, 3733, 5227, 5233, 5237, 5273, 5323, 5333, 5527, 5557, …

A019546

English corner

The prime numbers are natural numbers, like 2, 3, 5, 7, 11, . . . , which are not multiples of any smaller natural number, except 1. A prime number is any number whose only factors are 1 and itself. A prime number can be divided evenly only by 1, or itself. And it must be a whole number greater than 1. A prime number (or prime integer, often simply called a "prime" for short) is a positive integer p>1 that has no positive integer divisors other than 1 and p itself. More concisely, a prime number p is a positive integer having exactly one positive divisor other than 1, meaning it is a number that cannot be factored. – Wolfram MathWorld The Fundamental Theorem of Arithmetic states that every integer n >1 can be represented as a product of primes in only one way, apart from the order of the factors. There are infinitely many prime numbers – Euclid (300 A.C.) The sieve of Eratosthenes – Eratosthenes (275–194 B.C.)

Devinette – Solution

Futé! La moyenne de deux nombres donne un nombre qui est compris entre ces deux-là. S'agissant de premiers consécutifs, il n'y pas d'autres premiers entre ces deux-là.

Retour

Voir	Barre magique Nombres premiers – Index Semi-premiers FAQ sur les nombres premiers
	Nombres premiers – Table Ératosthène Facteurs premiers autour de 1000 Nombres composés Premiers en tableaux, en spirales … Programmation du crible d'Ératosthène Recherche des premiers avec un tableur Représentation des nombres
Site	La page des nombres premiers de Chris Caldwell – La référence du domaine
Calcul en ligne	A Primality Test – Prime Curiosity – Chris Caldwell – Savoir si un nombre est premier jusqu'à 10^16 Integer factorization calculator – Alpertron – Dédié aux très grands nombres; factorisation et autres nombreuses fonctions
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Premier/introduc.htm

Renvois de liens du fait de la réorganisation de ces pages

Voir	§ Page sur les Propriétés des nombres premiers
Voir	§ Page sur le théorème fondamental de l'arithmétique
Voir	§ Page sur les questions ouvertes
Voir	§ Différence entre premiers
Voir	§ Petit théorème de Fermat
Voir	§ Conjecture de Goldbach
Voir	§ La page spéciale historique
HISTORIQUE	§ Connus depuis l'Antiquité § Sans cesse à la recherche d'un nouveau nombre premier plus grand § Puis vinrent les ordinateurs, et § la course aux records se poursuit de plus belle § Voir le dernier record