Structure de groupe - définition

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/03/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Outils mathématiques
Débutants Structure	GROUPES				Glossaire Ensemble
INDEX Structures algébriques Accueil Sommaire	Introduction	Triangles et carrés	Définition
		Types de groupes	Groupe cyclique		Nombres
		Sommaire de cette page >>> Définition >>> Identité >>> Inverse		>>> Associativité >>> Commutativité >>> Théorème de Lagrange >>> Historique

GROUPES

Notion bien pratique relative à une collection (ensemble) d'objets. Car à ce nom sont associées des propriétés systématiques. Elles sont reconnues une fois pour toutes. Pas besoin d'y revenir.

Si une propriété relative à un groupe est prouvée, elle s'applique à chaque individu (élément) du groupe.

Note: Ceux qui font de la programmation objet savent comme il est pratique d'avoir des objets dont la structure est définie une fois pour toute.

Les chiens ont tous en commun d'avoir quatre pattes, une truffe, une queue … Ils forment le "groupe" des chiens. Inutile de répéter à chaque fois la liste de leurs attributs.

La multiplication est un moyen commode de ne pas répéter des additions.

En maths, le groupe est une entité dont les propriétés sont connues une fois pour toute. Chacun des individus de la collection possède toutes ces propriétés sans avoir besoin de les redire à chaque fois.

Le groupe est un moyen commode de ne pas répéter certaines propriétés liées à une collection d'individus et à une action les concernant.

APPROCHE imagée
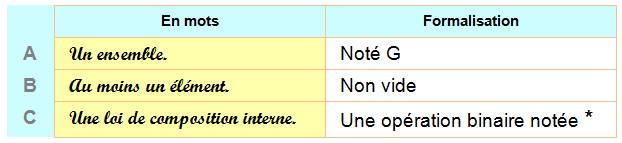
Les humains forment une collection d'individus. Un ensemble.
Avoir des enfants est une action qui à partir d'humains engendre des humains. Loi de composition interne.
Certains humains ont décidé de ne pas avoir d'enfants. Élément neutre.
Il y a des hommes et des femmes. Éléments opposés ou inverses ou symétriques
Les humains vivent en familles Associativité.
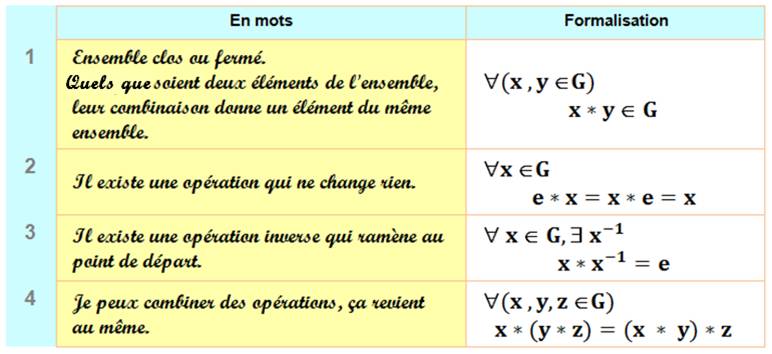
Analogie utilisée pour donner une première impression à propos des groupes. Ne pas vouloir pousser la comparaison trop loin! Nous allons préciser ce qu'est réellement un groupe en mathématiques.

GROUPE – Définition

Trois conditions

Binaire = opération entre deux élément pour en produire un troisième.

Loi de composition = opération.

Interne, car le résultat est un élément existant de l'ensemble.

En quatre points

Explications de ces notations ci-dessous

Notation

Le groupe g et son opération sont noté (G, *)

Définition classique

On appelle groupe tout ensemble (G, *) muni d'une loi de composition interne vérifiant les trois propriétés suivantes:

1. la loi * est associative;

2. (G, *) possède un élément neutre; et

3. tout élément de G est inversible pour la loi*.

Aussi: un groupe est un monoïde inversible.

Conséquence: élément neutre unique; chaque élément admet un inverse unique; tous les éléments sont réguliers pour la loi *.

IDENTITÉ et élément neutre

Élément qui ne modifie pas l'opération.

Quel que soit x appartenant à l'ensemble E, alors x composé à e est identique à e composé à x qui est identique à x seul.

Ex: Le nombre 0 est l'élément neutre de l'addition; et 1, celui de la multiplication.

L'élément e est appelé élément neutre ou identité du groupe (G,*). Il est unique.

Démonstration

SYMÉTRIQUE ou INVERSE

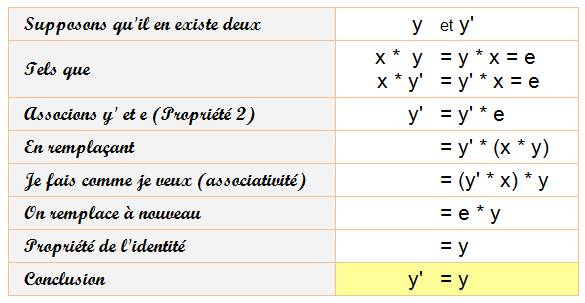
L'élément x^-1 est appelé l'inverse de x. Il est unique.

Soit un groupe (G,*) et un élément x de G;

il n'existe qu'un seul élément y de G tel que x * y = y * x = e.

Symétrique est le terme générique. Il devient "opposé" avec l'addition et "inverse" avec la multiplication. Inverse est fréquemment utilisé comme terme générique, surtout avec la formulation "inversible". On dit par exemple: tout élément de G est inversible pour la loi *.

Démonstration

ASSOCIATIVITÉ

x * y * z = x * (y * z) = (x * y) * z

Cette propriété est appelée associativité.

Dans le cas de cette opération particulière(*), les parenthèses sont inutiles.

Les OPÉRATIONS peuvent être effectuées dans l'ordre que l'on veut.

S'il n'y a que des additions, pas besoins de parenthèses; s'il n'y a que des multiplications, pas besoin de parenthèses; s'il y a les deux opérations, là les parenthèses sont importantes.

COMMUTATIVITÉ

Commuter veut simplement dire: échanger, intervertir.

Cette propriété n'est pas obligatoire pour constituer un groupe.

Si elle est présente, le groupe est dit commutatif ou abélien.

x * y = y * x

Cette propriété est appelée commutativité.

Dans ce cas, et dans ce cas seulement, on peut effectuer les opérations en prenant les ÉLÉMENTS dans l'ordre que l'on veut.
Attention: avec l'associativité ce sont les opérations qui peuvent être interverties.

Nils Henrik Abel (1802-1829)

Mathématicien norvégien connu pour avoir résolu le problème des équations quintiques en inventant la théorie des groupes.

Le prix Nobel en mathématique n'existe pas. Le prix Abel a été créé en 2001 par le Gouvernement norvégien.

Théorème de Lagrange

Notion avancée

Pour un groupe G fini, et pour tout sous-groupe H de G, le cardinal (ordre) de H divise le cardinal de G :

card (H) card (G)

Le quotient du cardinal de G par le cardinal de H s'appelle l'indice de H dans G, il est noté :

card (G) = card (H) x card (G : H)

Voir Lagrange

Historique

1771: Étude des équations algébriques par Joseph-Louis Lagrange.

1832: Évariste Galois (1811-1832) s'intéresse aux permutations de l'ensemble des racines d'un polynôme; Il met en évidence de nombreuses propriétés de ce qui est appelé de nos jours le groupe symétrique à n éléments. Ses travaux, dont la rédaction date de la nuit de son duel funeste, seront publiés après sa mort en 1846.

Cauchy (1789-1857) s'intéresse aux permutations et pose les bases de la théorie des groupes (sans que ce soit ainsi nommé à son époque).

L'intérêt de la notion de groupe devient plus claire avec la géométrie (Félix Klein) puis la théorie des nombres (Euler et Gauss).

Seconde moitié du XIX^e siècle et début du XX^e siècle, la théorie des groupes est mises au point par Cayley (table de Cayley), Weber, Frobenius, Burnside.

Encore aujourd'hui, la théorie des groupes suscite de nombreux travaux avec des applications partout où se niche la symétrie: cristallographie, chimie, théorie de la relativité, physique des particules et, plus généralement, physique quantique, etc.

Retour	Groupe – Introduction
Suite	Anneaux Corps Groupe – Nombres Groupe monstre Groupes – Types Groupes cycliques Groupes et triangles Outils mathématiques – Index Classes de congruence Classes de congruence avec diviseurs de n
Voir	Calcul – Index Constructions des ensembles de nombres Ensemble – Glossaire Géométrie – Index Groupe fondamental Jeux et puzzles – Index Les symétries Les types de nombres Logique – Index Théorie des nombres – Index
Cette page	http://villemin.gerard.free.fr/Referenc/Outils/AOUTILS/Groupe.htm