|
Édition du: 10/02/2024 |
|
INDEX |
Polygones |
||
|
Polygones
– Propriétés |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
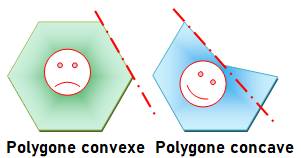
Polygones CONCAVES Polygones non-convexes, polygones
rentrants Définition,
propriétés et curiosités. Pavage du
sphinx. |
||
|
|
Sommaire de cette page >>> Approche >>> Propriétés >>>
Somme des angles >>>
Défis >>>
Pavage |
Débutants Glossaire |
Anglais: Concave polygon
|
Types de polygones
CONVEXE
CONCAVE CROISÉ |
||
|
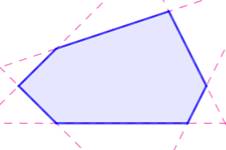
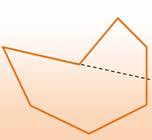
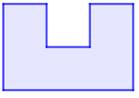
Polygone concave – Définition Polygone
tel qu'il existe deux points du polygone reliés par un segment
non-entièrement contenu dans le polygone. Voir le trait pointillé sur l'illustration |
|
|
|
Type Polygone non-convexe et
non-croisé. Tous les polygones concaves sont irréguliers. Le triangle
(3-gone) n'est jamais concave. Sommet Polygone tel qu’un sommet est tournée vers
l’intérieur du polygone. Côtés Un polygone concave doit avoir au moins quatre
côtés. Diagonales Certaines diagonales peuvent se trouver
partiellement ou complètement à l'extérieur du polygone concave. De même, il existe des sécantes qui coupent le
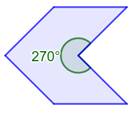
polygone plus de deux fois. Angles Les polygones concaves ont au moins un angle interne
rentrant (> 180°). L’angle rentrant fait pointer le sommet vers
l’intérieur. Les angles intérieurs ne sont pas égaux. |
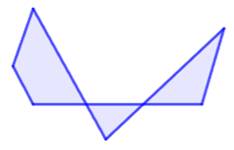
Concave et convexe
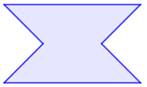
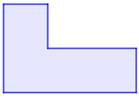
Exemples de polygones concaves
|
|
|
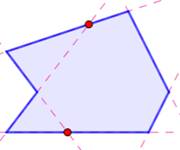
Propriété La sommes
des angles internes d'un polygone concave à n côtés, comme pour les
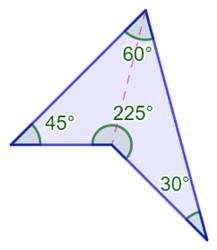
polygones concaves, est égale à: Exemple (figure) Explication Le polygone est divisé en deux triangles
(pointillé). La somme
des angles de chacun est 180°. La somme des angles externes est quelconque et
peut être supérieure à 360°. |
|
|
|
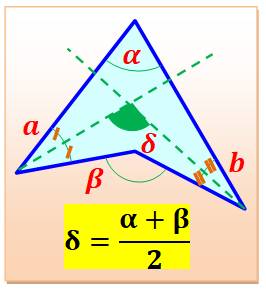
Avec les bissectrices Un quadrilatère concave. Les bissectrices des angles voisins de l'angle
interne rentrant. L'angle
entre bissectrices est la demi somme des angles alpha et bêta. Explication
|
|
|
Voir Poster
– Triangles
|
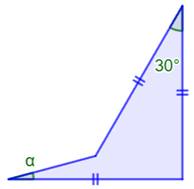
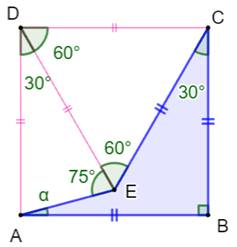
Construction du défi n°1 Un quadrilatère concave avec trois côté
isométriques. Un angle vaut 30° Quelle est la valeur de l'angle alpha ? Piste La somme des angles internes du quadrilatère vaut
360°. On connait les angles en B et C, on cherche l'angle en A. Il faut donc
connaitre l'angle en E. Pour cela on complète le carré. Solution L'angle DCE est égal à 90° – 30° = 60°. Dans le carré: DC = BC. Le triangle CDE est équilatéral. L'angle en E
vaut 60°. Finalement l'angle externe en E vaut: 75° + 60° =
135° et l'angle interne: 360° – 135° = 225° Dans le quadrilatère bleu: |
Figure du défi
Construction et notations
|
|
|
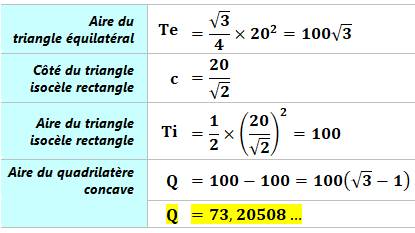
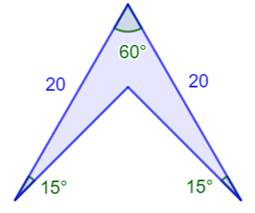
Construction du défi n°2 Quelle est l'aire de ce quadrilatère concave en
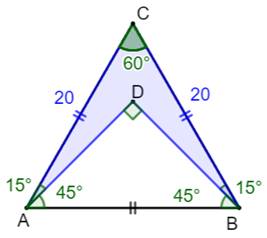
forme de delta ? Piste Complétons le triangle équilatéral ABC. Ses côtés
sont connus, son aire s'en déduit. Le triangle ADB possède deux angles de 45° (60° –
15°). Il est isocèle
rectangle. Sa base est connue, son aire s'en déduit. Calculs
|
Figure du défi
Construction et notations
|
Voir Défis en
géométrie – Index
|
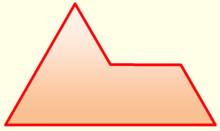
Avec cette brique pentagonale concave, dite du
sphinx, dans ce sens ou retournée, il est possible de paver le plan
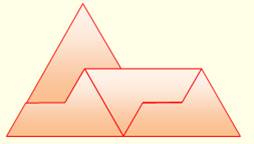
infini. Avec quatre de ces briques, il est possible de
reconstituer une brique plus grande de même forme (homothétie
de rapport 2) Ave cette nouvelle brique, il est possible d'en
construire une nouvelle plus grande, etc. C'est une composition en mode fractal
ou autosimilarité. Un puzzle avec cette brique est diffué par le
fabricant EFCÉ. |
|
||
|
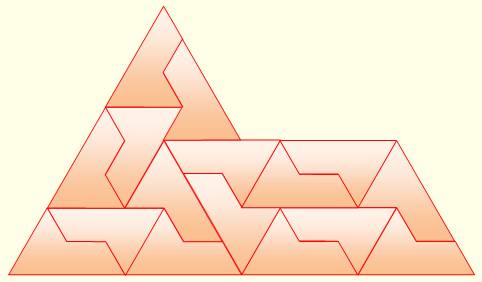
En restituant la brique de base en plus grand,
puis encore en plus grand, etc. 16 briques |
|
||
|
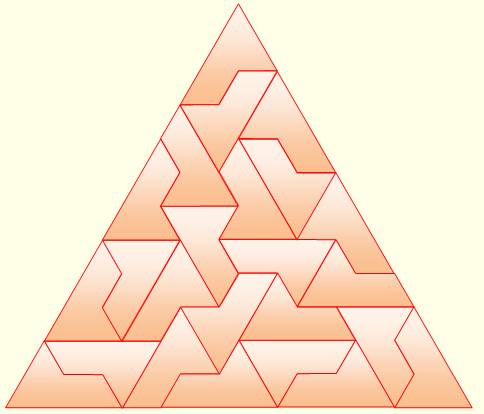
En construisant un triangle équilatéral, puis un
plus grand, puis de plus en plus grand. 24 briques |
|
||
Haut de page (ou double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/PolyCave.htm
|