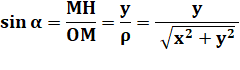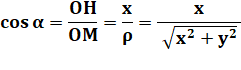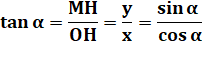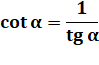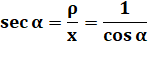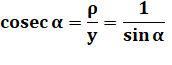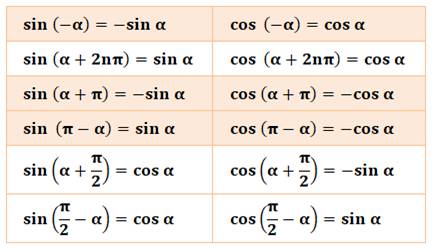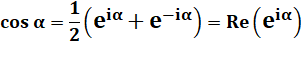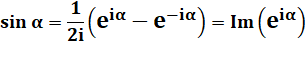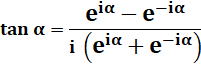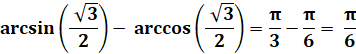NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths

Analyse

Débutants Général

TRIGONOMÉTRIE

Glossaire Général

INDEX Outils de trigo Trigonométrie Analyse Identités

Débutant

Introduction

En pratique

Angles

Valeurs

IDENTITÉS GÉNÉRALES

Angle triple

Angles multiples

Addition d'angles

Linéarisation

Tangente

Cosécante

Calculs

Cours première

Angles A, B et C

Euler–Moivre

Pi/5 = 36°

Démonstrations des identités

Calculs particuliers

Pi / n

Nbs transformés

Pi / 8 = 22,5°

Pi / 9

Pi / 7

Réciproques – arcsin, arccos, arctan

Sommaire de cette page >>> Définitions >>> Lignes trigonométriques entre elles >>> Relations entre angles cousins >>> Relations d'Euler >>> Développement en série de sinus, … >>> Formules en 1 >>> Angle moitié >>> Angle double >>> Angle triple >>> Addition d'angles >>> Addition converties en produits >>> Produits de valeurs trigonométriques >>> Arcsin et arccos

IDENTITÉS TRIGONOMÉTRIQUES

Formulaire

Formules classiques (lycée) et moins classiques (pages suivantes), avec leurs démonstrations.

Voir Table des valeurs trigonométriques / Les angles particuliers un par un

sin² A + cos² A = 1

Voir Pensées & humour

Définitions
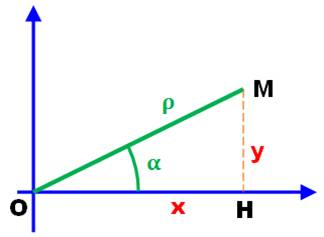
Le COsinus est à CÔté de l'angle Notez: tangente abrégée en français en tg, et tan en anglais; cotangente en cotg et cot. La normalisation internationale irait vers tan et cot.	Théorème de Pythagore x² + y² = = 1 cos² + sin² = 1 Voir Démonstration de cette relation sans Pythagore

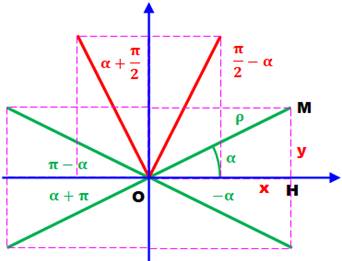
Voir Valeurs des lignes trigonométriques selon l'angle

Représentation graphique

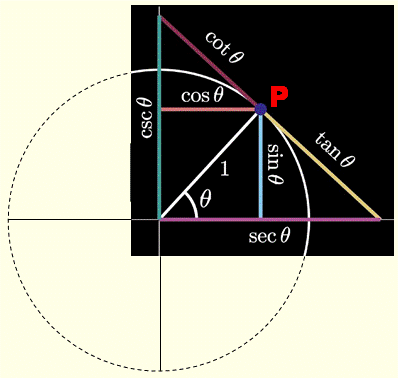
Voir Mémorisation avec l'hexagone magique

Lignes trigonométriques entre elles

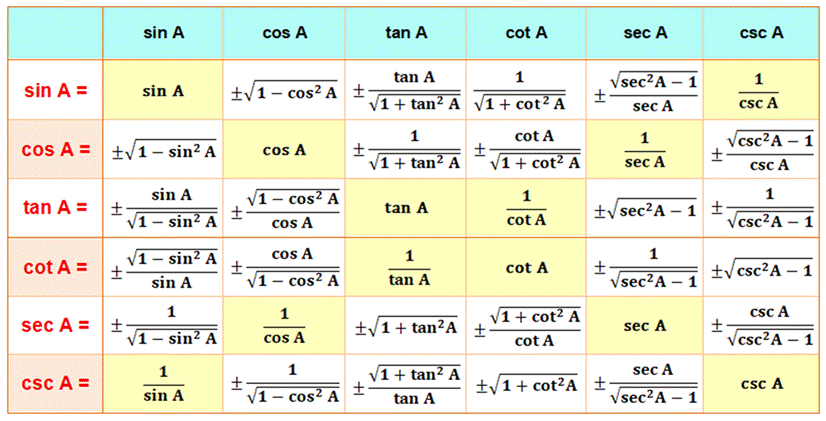
Merci à Nicolas Bocquel pour ses remarques

Relations entre angles cousins
Aide à la mémoire: cosXinus en x et sYnus en y Remarque: inutile d'apprendre ce genre de tableau par cœur, un petit dessin suffit à retrouver les valeurs.

Voir Application en Brève 786

Relations d'Euler
Avec a = x + i y =>

Voir Nombres complexes / Forme exponentielle des nombres complexes

Développement en série de sinus, de cosinus, de tangente et de cotangente

Voir Limite de sinus(x)/ x

Formules en 1 – Relations pythagoriennes
Produits	sin A . cosec A sec A . cos A tan A . cot A	= 1
Carrés Sinus & cosinus	sin² A + cos² A	= 1 Autre forme >>>
Tangente et cotangente		= 1 + tan^2 A = 1 + cotan^2 A
	sec² A + cosec² A	= 2 + tan² A + cot² A

Angle moitié
Sinus	2 sin² A/2	= 1 – cos A
Cosinus	2 cos² A/2	= 1 + cos A
Tangente	tan A/2

Pour les angles de 0 à Pi et avec t = tan (A/2)	sin(A)
	cos(A)
	tan(A)

Tableau complet >>>

Merci Bernard P.

Angle double
Sinus	sin 2A	= 2 sin A . cos A
	sin² A
	1 + sin 2A	= (cos A + sin A)^2
	1 – sin 2A	= (cos A - sin A)^2 >>>
Cosinus	cos 2A	= cos² A – sin² A = 1 – 2 sin² A = 2 cos² A – 1
	cos² A
Tangente	tan 2A

Tableau complet >>>

Angle Triple
Sinus	sin 3A	= 3 sin A – 4 sin^3 A Voir Démo
Cosinus	cos 3A	= – 3 cos A + 4 cos^3 A Voir Démo
Tangente	tan 3A

Tableau complet >>>

Angles ntuples >>>

Addition d'angles
Sinus	sin (A + B) sin (A – B)	= sin A . cos B + cos A . sin B = sin A . cos B – cos A . sin B Voir Démo
Cosinus	cos (A + B) cos (A – B)	= cos A . cos B – sin A . sin B = cos A . cos B + sin A . sin B
Produits	sin (A + B) . sin (A – B)	= sin² A – sin² B = cos²B – cos² A
	cos (A + B) . cos (A – B)	= cos² A – sin² B = cos²B – sin² A
Tangente	tan (A + B)
	tan (A – B)

Tableau complet >>>

Cas où A + B + C = Pi >>>

Additions converties en produits – Factorisation
Formules de Prosthaphaeresis ou de Simpson
Sinus	sin A + sin B	= 2 sin ½ (A + B) . cos ½ (A – B) Voir Démo
	sin A – sin B	= 2 sin ½ (A – B) . cos ½ (A + B)
Cosinus	cos A + cos B	= 2 cos ½ (A + B) . cos ½ (A – B)
	cos A – cos B	= 2 sin ½ (B – A) . sin ½ (A + B) = – 2 sin ½ (A – B) . sin ½ (A + B)
Tangente	tan A + tan B tan A – tan B	= sin (A + B) / cos A . cos B = sin (A – B) / cos A . cos B

Tableau complet >>>

Produits de valeurs trigonométriques – Linéarisation
Sinus et cosinus	2 sin A . sin B 2 cos A . cos B	= cos (A – B) – cos (A + B) = cos (A – B) + cos (A + B)
Mixte	2 sin A . cos B 2 cos A . sin B	= sin (A + B) + sin (A – B) = sin (A + B) – sin (A – B)

Voir Application au triangle isocèle / Multiplication avec ces identités (Prosthaphaeresis)

Puissances et linéarisation >>>

"Pour la route": quand 3 se transforme en 2 avec la trigo …

Voir Nombres entiers transformés

Arcsin et Arccos – Quelques sommes

Voir Fonctions réciproques – Formulaire / Calculs avec arcsin et arccos

Bases	Trigonométrie – Débutant Trigonométrie – Tables Relations dans le triangle quelconque Relations dans le triangle rectangle
Suite	Angle en Pi/7 Formules avancées Angle multiple Puissances Trigonométrie sphérique
Voir	Angles et informations concernant un angle particulier Faire le tour du cercle (relations de base) Sinus et aire du triangle isocèle Calculs en trigonométrie (simples) Calculs en trigonométrie (avancés) Formulaires – Index Linéarisation: puissances des fonctions trigonométriques Relations trigonométriques dans le triangle quelconque
Aussi	Triangle Pentagone Identités remarquables
Maple	Avec ce logiciel, l'instruction trigsubs (tan (x/2) ), par exemple, vous donne toutes les identités connues pour tangente (x/2).
Sites	Identité trigonométrique – Wikipédia List of trigonometric identities – Wikipedia Proofs of trigonometric identities – Wikipedia Trigonométrie circulaire – Jean-Louis Rouget – les formules du lycée à savoir pour aborder le supérieur. Introduction to trigonometric functions – Wolfram Research – Pour experts !
Cette page	http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/Relation.htm