|
Édition du: 01/06/2025 |
|
INDEX
|
TOPOLOGIE |
||
Faites un double-clic pour un retour en haut de page
![]()
|
topologique Comment
passer d'un objet en un autre en le découpant finement et en recollant les
morceaux ? En topologie,
traduire objet ou surface par le mot dédié: variété. La
chirurgie topologique est une technique fondamentale en topologie
différentielle et en géométrie. Elle est utilisée pour modifier les variétés
de manière contrôlée. Le but étant de transposer les propriétés d'une variété
plus simple à une variété plus compliquée. |
||
|
|
Sommaire de cette page >>> Approche >>> Historique et intérêt >>> Chirurgie du tore transformé en sphère |
Débutants Glossaire |
|
Principe La chirurgie topologique est un procédé qui
transforme un objet en un autre en le découpant en menus morceaux, puis en
les recollant de manière à composer la forme finale voulue. |
Exemple de la sphère Une sphère est une surface sans coin ni
bord, et sans trou (elle est dite
simplement connexe). La chirurgie topologique sur la sphère se déroule
en deux étapes principales: la découpe et
le recollement |
|
|
La Découpe La première étape consiste à retirer une partie
de la sphère. Pour ce faire, on choisit une région qui
ressemble à un disque ouvert. Un disque ouvert peut être imaginé comme
une zone circulaire dans le plan sans inclure la bordure. Autrement dit, tous
les points à l’intérieur du cercle sont pris en compte, mais la frontière
circulaire n’en fait pas partie. La découpe de la sphère crée alors une
coupure ou un bord (la
frontière de la région retirée) qui est en fait un cercle fermé. Grâce à cette découpe, la sphère se transforme en
une surface à bord (comme une sorte de
capote élastique ouverte) tout en gardant l’essence de sa structure globale. |
Le Recollement La seconde étape est celle du recollement. Le bord ainsi que nous avons
obtenu est recollé de manière contrôlée. Le procédé peut impliquer une
rotation ou une déformation avant que les extrémités ne soient réunies. Ce recollage n’est pas anodin. En effet, s’il est
effectué de manière directe (sans modification), l’objet obtenu reste homéomorphe (du même type topologique) à la sphère
d’origine. Cependant, si l’on introduit une torsion avant de
recoller le résultat peut être radicalement différent (objets topologiques
exotiques). |
|
|
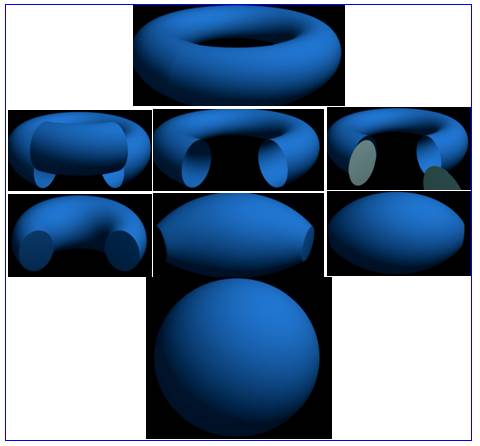
Changement de genre par chirurgie On parle de chirurgie parce que l’on modifie la structure intrinsèque de la
surface par une opération locale qui peut changer le genre
de la surface. Par exemple, en recollant avec une rotation
particulière, on peut ajouter une anse
à la surface, transformant ainsi la sphère en un tore. Soit: en
passant du genre 0 au genre 1. |
Définitions Disque ouvert : Ensemble
des points à l’intérieur d’un cercle sans inclure le cercle lui-même. Bord : Limite d’une
région, ici, le cercle formé suite à la découpe. Genre : Quantité de
trous dans une variété (une surface). |
|
|
La chirurgie topologique, introduite par Milnor
et Wallace dans les années 1960, est une méthode pour transformer une variété
en une autre en enlevant une partie de la variété et en la remplaçant par une
autre partie. Cette technique est particulièrement utile pour
classifier les variétés et étudier leurs propriétés. |
La chirurgie topologique est un outil puissant et
essentiel en topologie et en géométrie. Elle est non seulement cruciale pour la
classification des variétés, mais elle ouvre également de nouvelles voies
pour la recherche en mathématiques et en physique théorique. |
||
|
1961 |
Introduction
de la chirurgie topologique par John Milnor.
John Milnor est un mathématicien américain né en
1931, connu pour ses travaux en topologie
différentielle. |
||
|
1963 |
La classification des sphères exotiques par
Kervaire et Milnor en 1963 amena à l'émergence de la chirurgie comme un outil
majeur de la topologie en grande dimension. René Thom et John Milnor démontrent que certaines
sphères de dimension supérieure à 4 possèdent des structures différentielles
exotiques. Cette découverte renforce l'importance de la chirurgie dans
l'étude des variétés différentiables. |
||
|
1970 |
Développement de la théorie de la chirurgie en
dimension 4. Michael Freedman et William Browder étendent la
chirurgie aux variétés de dimension 4, un cas particulièrement complexe. Ces
travaux permettent de mieux comprendre les structures différentiables et
topologiques en dimension intermédiaire. |
||
|
1982 |
Preuve du théorème de classification des
4-variétés par Freedman Freedman prouve que toute 4-variété simplement
connexe est classifiable par des invariants topologiques. Cette avancée
repose sur des techniques de chirurgie et révolutionne la compréhension des variétés
de dimension 4. |
||
|
1985 |
Application de la chirurgie à la conjecture de
Poincaré en grande dimension Stephen Smale démontre la conjecture de Poincaré
en dimension supérieure à 4 en utilisant des techniques de chirurgie. Cette
preuve établit un lien fondamental entre chirurgie et classification des
variétés. |
||
|
1994 |
Développement de la chirurgie
en topologie symplectique. Les travaux de Donaldson et Gompf montrent
comment la chirurgie peut être utilisée pour construire des variétés
symplectiques complexes. Cette approche ouvre de nouvelles perspectives en
géométrie différentielle. La topologie
symplectique est une branche des mathématiques qui étudie les
structures géométriques utilisées notamment en mécanique classique et en
physique quantique. Pour l'expliquer simplement, imagine un tapis en
caoutchouc que tu peux étirer et déformer sans le déchirer ni le plier
brusquement. La topologie symplectique s'intéresse aux propriétés qui restent
inchangées sous ces transformations. |
||
|
2003 |
Preuve de la conjecture de Poincaré en dimension
3 par Perelman. Bien que la preuve de Perelman repose
principalement sur la théorie de Ricci et la géométrie différentielle, la
chirurgie joue un rôle clé dans la compréhension des structures topologiques
des 3-variétés. |
||
|
2010 |
Applications de la chirurgie en topologie des
feuilletages. Les techniques de chirurgie sont utilisées pour
modifier les structures de feuilletage sur les variétés, permettant une
meilleure classification des espaces fibrés et des structures dynamiques. Les structures de
feuilletage en topologie sont une manière d'organiser un espace en couches ou
en "feuilles" qui se superposent sans se croiser. Imagine un livre
ouvert, où chaque page représente une feuille d'un feuilletage : bien que les
pages soient distinctes, elles forment ensemble une structure cohérente |
||
|
2015 |
Chirurgie et topologie quantique. Les chercheurs explorent l'utilisation de la
chirurgie dans la topologie quantique, notamment pour la classification des
états topologiques en physique théorique. |
||
|
2023 |
Avancées en chirurgie des variétés de dimension
infinie. Les travaux récents montrent comment la chirurgie
peut être généralisée aux espaces de dimension infinie, ouvrant des
perspectives en analyse fonctionnelle et en géométrie non commutative. |
||
|
John Milnor, Michel Kervaire et William Browder
ont montré que dans presque toutes les dimensions, toute variété peut être
convertie en une sphère exotique par un procédé appelé chirurgie. Lors de cette opération:
|
|
|
Voir Brève
63-1242
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |