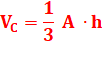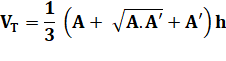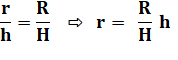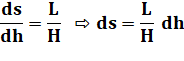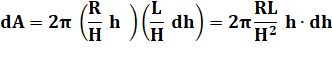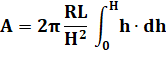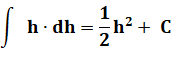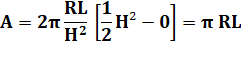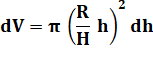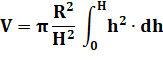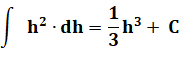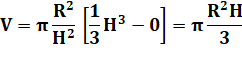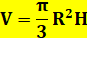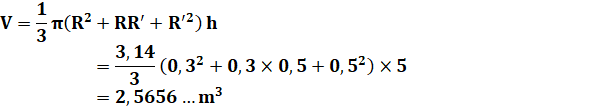NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 30/07/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	OBJETS 3D
Débutants Géométrie	CÔNE de RÉVOLUTION				Glossaire Géométrie
INDEX Géométrie	Présentation	Calculs – Cône	Calculs – Tronc de Cône	Équations
			Cône elliptique
		Sommaire de cette page >>> Approche >>> Cône en général >>> Mesures – Cône oblique >>> Mesures – Cône droit >>> Aire latérale du cône par intégration >>> Volume du cône par intégration >>> Exemple de calcul: la bille de bois >>> Section du cône >>> Anglais >>> Art! anamorphose conique

CÔNE de RÉVOLUTION Présentation Le cône, une pyramide à base circulaire. Cônes en biologie: cellule visuelle de la rétine, déterminant la perception des formes et des couleurs. Mnémotechnique: COCO pour COnes COuleurs; les bâtonnets, eux, sont sensibles à la lumière mais pas à la couleur. Cônes en zoologie: gastropode marin carnassier et venimeux. Formules découvertes par Démocrite. Prouvées par Eudoxus

Approche
Un cône est formé par une droite mobile passant par un point fixe en s'appuyant sur une courbe donnée. Dans le cas du cône usuel : La courbe est un cercle, L'axe du cône passe par le centre du cercle et, il est perpendiculaire au plan contenant ce cercle. C'est un cône de révolution (ou circulaire droit).
Un cône de révolution est un solide composé d’un disque de base, d’un sommet appartenant à la perpendiculaire au disque de base passant par le centre de ce disque et d’une seule face latérale, non plane. Un cône de révolution est un solide que l'on peut créer en faisant pivoter un triangle rectangle autour d'un des côtés de l'angle droit. La base du cône de révolution (sa directrice) est un disque. Le sommet du triangle autour duquel il pivote pour former le cône est le sommet du cône. Le segment portant l'axe de rotation est la hauteur. L'hypoténuse du triangle rectangle, ou apothème du cône, engendre (développe) une surface dite surface latérale du cône (ou développement du cône). La surface latérale peut être déroulée dans un plan. On obtient alors un secteur circulaire.

NB Le disque est la surface délimitée par un cercle

Cône en général
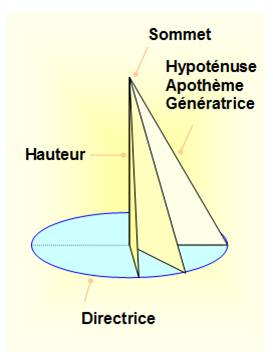
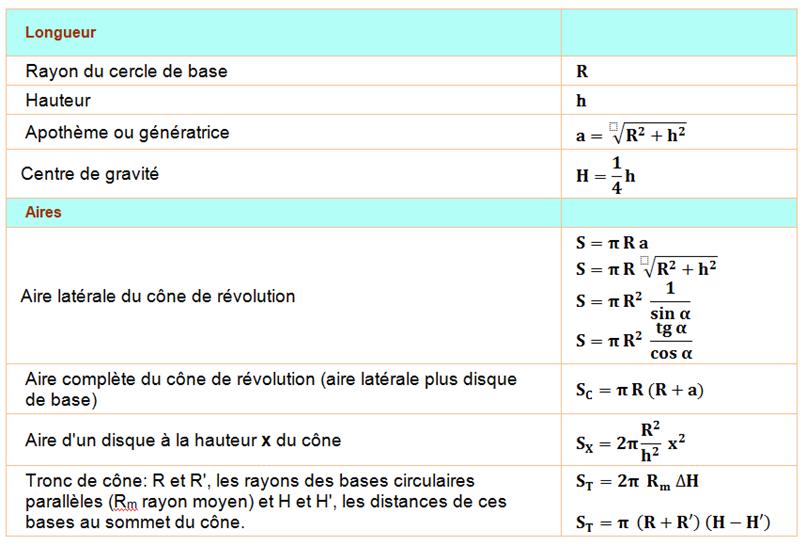
Une courbe dans un plan: la directrice du cône. Un point S extérieur au plan: le sommet du cône. Toutes les droites (génératrices) passant par S et s'appuyant sur toute la longueur de la directrice engendrent une surface conique. Définition Cône: surface réglée dont les génératrices passent par un point fixe appelé sommet du cône. Un cône est parfaitement déterminé par son sommet et une courbe de sa surface rencontrant toutes les génératrices, appelée directrice du cône. Oblique et droit La directrice est une courbe plane fermée. C'est la base du cône. Son plan est situé à une distance h du sommet. Si l'axe est perpendiculaire à la base, le cône est droit Si la base est un cercle, c'est un cône de révolution, Si l'angle au sommet vaut 90°, le cône est rectangle (hauteur = rayon). Si la hauteur est plus grande: cône acutangle, Si la hauteur est plus petite: cône obtusangle. Sinon, il est oblique ou scalène.	Cône oblique Cône de révolution

Mesures – Cône oblique
Volumes Volume du cône usuel (base d'aire A): Tronc de cône usuel (bases A et A', hauteur h):
Rappel Le volume d'une pyramide est égal au TIERS de celui du prisme qui la contient Anglais: there is a nice result in geometry which says that if you take a region in the plane which has an area, a point P not in the plane and form a "tent" by joining every point on the boundary of the region to the P then the volume of the tent is: 1/3 x the area of the region at the base x the height of the tent.

Mesures – Cône de révolution (droit)
Voir exemple de calcul pour le cône / pour le tronc de cône

Aire latérale du cône par intégration
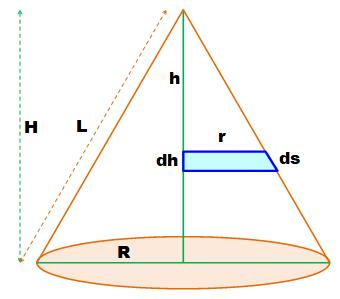
Pour procéder au calcul de l'aire latérale du cône par intégration, on identifie une tranche de cône d'épaisseur dh dont on va calculer la surface latérale Celle-ci varie en fonction de sa position pour h allant de 0 à H. Son épaisseur est dh. Elle est aussi fine qu'on le désire. Il est légitime de prendre le rayon moyen r.
Valeur de r:
Hauteur latérale de la tranche:
Aire latérale de cette tranche:
Seuls h.dh est variable et va subir l'intégration.
La primitive d'une fonction linéaire est du second degré.
Calcul de l'intégrale: valeur finale diminué de la valeur initiale.
La distance oblique est connue.

Volume du cône par intégration
Volume de la tranche cylindrique:
Seuls h².dh est variable et va subir l'intégration.
La primitive est du troisième degré.
Intégration par parties: valeur finale diminué de la valeur initiale.
Finalement:

Voir Volume des solides de révolution

Exemple: la bille de bois:

Problème

Une bille de bois (grume) mesure 5 m de long et à ses extrémités les sections circulaires font 30 cm et 50 cm de rayon. Quel est le volume de bois? De la poutre à section carrée que l'on peut en tirer? Et pour deux poutres de 2,5 m de long?

Calculs

Volume de la bille de bois:

Pour vérification et comparaison, volume des deux cylindres

Poutre à section carrée. La section carrée doit être inscrite dans le petit cercle de 30 cm. Côté du carré: 302 cm. Et le volume de la poutre:

Avec deux poutres carrées de 2,5 m de long. La première poutre s'inscrit toujours dans le petit cercle de 30 cm; la seconde dans un cercle à mi-distance des extrémités, soit 40 cm.

Cas de deux poutres de section circulaire de 2,5 m de long

Résumé

Section du cône
Section du cône par un plan parallèle à la base perpendiculaire à la base quelconque	Un cercle. Deux droites obliques. Une conique (voir développements).

English corner

A right circular cone is a solid generated by the revolution of a right-angle triangle about one of the sides containing the right angle as axis.

The point at the top is called the vertex, and the angle (which is twice the angle of the revolving triangle is the vertical angle.

Allemand et hollandais: Kegel

Espagnol: Cono, bolse

Italien: Birillo, cartoccio

Cône Cône de révolution En forme de cône Tronc de cône	Cone Circular cone Right-circular cone Cone-shaped Truncated cone Frustum (of cone) Conical frustum
Sommet Angle au sommet Demi-angle au sommet Axe du cône Hauteur Directrice Génératrice Hypoténuse Apothème Base Surface latérale	Vertex Vertical angle Cone aperture Semi—vertical angle Cone axis Height Altitude Directrix Generating line Hypotenuse Slant height Base Lateral surface Curved surface
Cornet à glace	Ice-cream cone

Anamorphose conique

Cliquez pour taille réelle

Auteur: Denis Locquet

Suite	Amusements avec les cônes Calcul du volume d'un cône à section elliptique Coniques
Voir	Cercle Cône, demi-sphère et cylindre Cylindre – double-cône = sphère Coniques Coniques – Théorème de Pascal Cône et triangle rectangle Cônes et démonstration du théorème de Monge Cylindre Pyramides Vocabulaire de la géométrie
Sites	Cône de révolution (et plus) Cône – Homeomath Surfaces coniques Cone – from Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/GeomLAV/Objet3D/Cone.htm