![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page |
|
22 Novembre 2025
![]()
|
Édition du: 29/11/2025 |
|
INDEX lettre M |
Dictionnaire de base du vocabulaire des mathématiques |
|
|
Faites
un double-clic pour un retour en haut de
page
Pour
trouver un mot: Ctrl F et tapez le mot
cherché
|
Avertissement Dictionnaire pour débutants,
juniors, novices, "nuls" … !!! On privilégie la compréhension par rapport à une rigueur mathématique !!! Les liens permettent de compléter et d'approfondir Pour une
version plus académique se reporter aux ouvrages spécialisés |
Légende Parfois,
plusieurs définitions sont données: de la plus "intuitive" à la
plus correcte mathématiquement Mode de recherche: si vous ne trouvez
pas symétrie centrale à symétrie, voyez à centrale, par exemple. Difficulté: * notion avancée;
** notion complexe. |
![]()

Voir Nombre 11
M: vaut 1000 en chiffres
romains; M symbole de méga; m symbole de milli.
– v. Lettres comme symboles en mathématiques.
– a. M equals 1000 in Roman numerals.
Machine: appareil
remplissant une certaine fonction.
Machine de Turing** machine fictive à
la base de la théorie des automates.
– v. Machine
de Turing / Automate
– a. Turing machine
Machine proposée par Alan Turing en 1936, avant
l'avènement des ordinateurs. Bien que simple, cette machine peut simuler tout
type d'algorithme, quelle que soit sa complexité.
Magique
(carré -): grille de nombres dont toutes lignes, colonnes et diagonales ont la même
somme.
– v. Carrés
magiques
– a. Magic square
Magma*: Structure
d'ensemble la plus basique: ensemble muni d'une opération la plus générale,
noté (E, *)
– v. Vocabulaire
des structures algébriques, Amas
– a. Magma; Voir Types de
magmas (Wikipedia)
Magnitude: grandeur, ampleur
– ex. la magnitude d'un séisme, la magnitude apparente
d'un astre.
– a. Magnitude: the size or value irrespective of sign.
The magnitude of any number is usually called
its absolute
value or modulus, denoted by ![]() .
.
Magnitude (en anglais):
taille, grandeur, amplitude, envergure, portée
– Taille ou ampleur (absolue ou relative) d'une chose.
– Order of magnitude: ordre de grandeur.
– un nombre-référence associé à une chose pour besoin de comparaison numérique.
– Norme d'un vecteur.
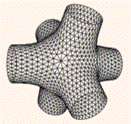 Maillage: réseau appliqué à un plan ou un espace.
Créations de cellules, de zones avec frontières. Discrétisation de l'espace. –
v. – syn. Pavage
Maillage: réseau appliqué à un plan ou un espace.
Créations de cellules, de zones avec frontières. Discrétisation de l'espace. –
v. – syn. Pavage
– a. Mesh
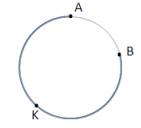
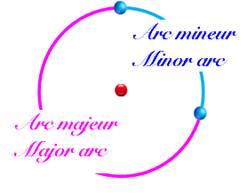
Majeur (arc - de grand
cercle): le plus grand des deux arcs compris entre deux points donnés d'un cercle.
– v. Arc mineur
– a. Major arc
Majorant: valeur supérieure à
celle donnée ou à toutes celles données.
On dit que a est un majorant de A, si tout élément de A est inférieur ou égal à
a.
– notation: ![]()
–
cont. Minorant
– a. Upper and lower bounds
Mandelbrot Benoît* (1924-2010)
– c. Biographie / Fractale
Mandorle: figure géométrique
en forme d'amande. Intersection de deux cercles de même rayon, chacun passant
le centre de l'autre aussi appelé Vesica piscis (vessie de poisson).
Figure fréquente sur les monuments religieux.
–
étym. de l'italien mandorla, amande
– v. Vesica Piscis, géométrie de la lentille
– a. Mandorla: almond-shaped aureola
Manhattan (distance de
-) ou taxi-distance: déplacement en horizontal et en vertical dans un
quadrillage (un réseau), comme un taxi dans le quartier de Manhattan à New
York.
Une distance classique entre deux points est le segment de droite et c'est la
plus courte. La distance de parcours à travers un réseau est plus longue et il
y plusieurs chemin cours.
– v. Distance de Manhattan
– a.
Manhattan distance, taxicab distance, Manahattan geometry
Manifold: anglais pour variété, en topologie.
Mantisse:
Mantisse (d'un nombre décimal): dans le nombre décimal 123,456: 123
est la partie entière et 0,456 la mantisse.
Si le nombre est négatif, ça se complique un peu.
Pour -123,456 : la partie entière est 124 et la mantisse: 0,544.
– étym. du latin mantissa, surplus.
– v. Numération
décimale
 Mantisse (virgule flottante): nombre formé des
chiffres les plus significatifs du nombre à représenter. Dans 1,23 1010
: 1, 23 est la mantisse, appellation courante qu'il vaudrait mieux baptisé
signicande pour éviter la confusion avec 0,23 qui est la mantisse du même
nombre décimal.
Mantisse (virgule flottante): nombre formé des
chiffres les plus significatifs du nombre à représenter. Dans 1,23 1010
: 1, 23 est la mantisse, appellation courante qu'il vaudrait mieux baptisé
signicande pour éviter la confusion avec 0,23 qui est la mantisse du même
nombre décimal.
– v. Notation scientifique
– a. Mantissa, significand: part of a number in scientific notation or in
floating-point representation, consisting of its significant digits.
Mantisse (d'un logarithme): partie décimale,
toujours positive, d'un logarithme.
Même principe de complément que pour le nombre décimal. La partie entière est
la caractéristique.
– a. Mantissa: the decimal fraction part of a common logarithm. For example, log111 = 2.0453. Therefore, 2 is the characteristic and
.0453 is the mantissa.
Maple: un des logiciel de programmation pour les mathématiques.
Maxima: est une alternative gratuite à Maple.
– v. Outils de programmation
Masse: proche, mais à ne
pas confondre avec le poids.
Grandeur qui reflète la quantité de matière et donc la susceptibilité d'attirer
plus ou moins une autre masse de matière; elle se mesure à la force nécessaire
pour mettre en mouvement un corps ou à le faire changer de direction.
– v. Masse / Masse manquante
– a. Mass
Plus spécifiquement: quotient de la force
appliquée à un corps par l'accélération que cette force imprime au mouvement de
ce corps (masse inerte); grandeur qui caractérise un corps relativement à
l'attraction qu'il subit de la part d'un autre (masse pesante).
Unité SI: kilogramme (kg); contrairement au poids, la masse est indépendante du
lieu où la matière se trouve.
Masse volumique (ou densité volumique
de masse): masse d'un mètre-cube de matière.
– unité SI:
kg/m3
– a. Density, volumetric mass density: its mass per unit volume
Masse (nombre de -): nombre total de
particules (protons et neutrons) constituant le noyau d'un atome.
Masse atomique (unité de -): elle est définie
par rapport à celle du carbone-12, laquelle vaut exactement de 12 u.m.a unité
de masse unifiée), ce qui représente 1,660 539 066 60 (50) 10-27
kg ou 931,494 028 (23) MeV/c².
– v. Masse atomique
– v. Unified atomic mass (u) or dalton(Da)
Matériel
informatique: tous les équipements relatifs aux ordinateurs, à l'informatique.
– v. Ordinateur
– a. Hardware
Mathémagique: mot-valise forgé sur mathématiques et
magiques.
Amusement, émerveillement avec la magie des
mathématiques, des nombres.
Mathématiques: science du
raisonnement sur une matière abstraite, comme les nombres, les figures géométriques …
Les mathématiques pures traitent du monde abstrait des nombres, figures et
autres concepts.
Les mathématiques appliquées développent les outils mathématiques utiles à la
modélisation scientifique.
Les mathématiques "modernes" cherche une unification des différentes
disciplines en une science entièrement déductive, formelle et axiomatisée et
devient la mathématique.
– v. Mathématiques, branches
des mathématiques
– a. Mathematics
Mathlète: mot valise désignant les
adeptes de calcul mental.
Matrice*
tableau
de nombres, appelés éléments, considéré comme un tout et sur lequel on
définit des opérations comme en arithmétique classique;
Cet outil simplifie le calcul, notamment la résolution des systèmes d'équation,
ou les calculs des objets en images de synthèse.
– Exemples de matrices: ![]()
– v. Déterminant, transposée, unité (matrice -), trace
– a. Matrix, several matrices
Matrices circulante: matrice carrée dans
laquelle on passe d'une ligne à la suivante par permutation circulaire
(décalage vers la droite) des coefficients.
– a. Circulant matrix
Matrices compatibles: l'une a une
quantité de colonnes égale à la quantité de lignes de l'autre.
– v. Multiplication
de matrices
– a. Compatible matrices: the number of columns in the first matrix is equal to
the number of rows in the second matrix.
Matrice de transformation*: elle caractérise
une transformation
géométrique.
Elle permet de passer d'un point décrit par une matrice colonne à la matrice
colonne de son image
par la transformation.
Très utilisée dans le domaine des images calculées.
– a. Transformation matrix
Matroïde: un exemple vaut
mieux qu'une définition dans ce cas. Prenons une matrice qui définit un graphe et
dont les lignes indexent les sommets et les colonnes les arêtes. C'est un
exemple de matroïde.
Plus généralement, un matoïde définit des relations dans un cadre
d'indépendance linéaire. C'est le cas dans l'étude des graphes rigides de Laman.
– a. Matroid
Maximum: plus grand élément
d'un ensemble ordonné; la plus grande des valeurs d'une fonction sur un
intervalle donné.
– a. Maximum
Mécanique:
branche
de la physique: études des équilibres, des mouvements dans la nature, des
déformations.
Trois domaines: Mécanique rationnelle ou newtonienne, mécanique relativiste, mécanique quantique
– v. Mécanique / Physique
– a. Mechanics, an area of science concerned with the behaviour of physical
bodies when subjected to forces or displacements.
Médian: qui coupe en deux.
Triangle médian d'un triangle: triangle dont les sommets sont les
milieux des côtés du triangle d'origine.
–
v. Triangle
médian
– v. Médial triangle
Médiane d'une série
statistique: la
médiane partage la population en deux parties de même effectif: 50% des
individus ont une valeur du caractère (taille, âge …) inférieure ou égale à la
médiane, et 50% une valeur supérieure ou égale à la médiane;
À ne pas confondre avec la moyenne.
– v. Médiane / Statistique, quantile
– a. Median: the median of a set of numbers is the middle number, when the
numbers are in order.
Médianes du triangle: droites passant par
un sommet et le milieu du côté opposé; elles concourent au centre de
gravité, en partageant la médiane en 1/3 et 2/3; Suite en Médiane.
– a. Median: the median of a triangle is a line segment from a vertex to the
midpoint of the opposite side.
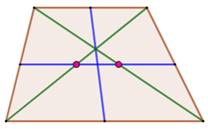
Médianes d'un quadrilatère: les deux segments
joignant les milieux des côtés opposés du quadrilatère.
– Propriété du trapèze: en bleu les médianes, et en vert les diagonales; les
deux points rouges, milieux des diagonales, sont situés sur une des médianes (Illustration).
– a. Median of a quadrilateral
Fraction médiane: à partir de deux
fractions, la fraction médiane est celle dont le numérateur est la somme des
numérateurs et idem pour le dénominateur. Avec 1/2 et 1/3, la fraction médiane
est 2/5. Propriété: la fraction médiane est toujours comprise entre les deux
fractions-mères (0,333… < 0,4 < 0,5).
Médiatrice: droite perpendiculaire à
un segment en son milieu.
Axe de symétrie
du segment; lieu des points à égales distance des extrémités du segment.
Les trois médiatrices du triangle concourent au centre du cercle circonscrit au
triangle.
– v. Médiatrice.
– a. Perpendicular (line segment) bisector of a given line.
Méga: facteur
multiplicatif par 1 000 000 = 106
– v. Million et méga,
préfixes (kilo,
méga …)
Membre: chacun des termes de part et
d'autre du signe égal.
Les deux membres de l'équation.
S'applique aussi à chacun des côté d'une inégalité.
– a. Member of an equation or side of an equation
Mémoire (informatique):
lieu
de stockage de l'information.
– v. Mémoire / Mémoire informatique
– a. Memory, computer memory
Ménélienne:
dans
un triangle, droite qui ne passe par aucun sommet.
– v. Céviennes
Mental: qui se fait de tête
comme le calcul mental.
– v. Technique de calcul mental
– a. Mental math, mental calculation, mental arithmetic: Mental math is math
that is done in your head, without writing or using a calculator or other
device.
Méridien:
plan qui passe par la
verticale d'un lieu et le centre de la Terre.
Aussi, le demi-cercle découpé par le plan sur la sphère terrestre.
– analogie: les plans méridiens
coupent la Terre comme des quartiers d'orange
– v. Sphère terrestre, longitude
– a. Meridian: a great circle (or semicircle) on the surface of the earth that
passes through both the north pole and the south pole and cuts the equator at
right angles. The prime meridian is the meridian that passes through Greenwich,
England.
Méromorphe (fonction -
)**: fonction holomorphe dans tout le plan complexe,
sauf éventuellement sur un ensemble de points isolés dont chacun est un pôle
pour la fonction.
– a. Meromorphic function
Mersenne (nombre de -):
nombre
de la forme Mn = 2n – 1.
Si le nombre de
Mersenne est premier
alors n est premier.
La réciproque est fausse.
Les plus grands nombres premiers connus sont des nombres premiers de Mersenne.
– a. Mersenne numbers, Mersenne prime. A Mersenne prime is a prime number that is one less than a power of two.
Mesure:
nombre
exprimant une quantité d'unités de mesure.
– v. Mesure, intensité,
module, grandeur
– a. Measure
Mesure algébrique: distance affectée
d'un signe entre deux points A et B (bipoint) sur une
droite orientée.
– ex. La mesure algébrique du bipoint (A, B) est le nombre réel k tel que ![]() est un vecteur
unitaire. Notation avec barre de surligement. Le segment étant noté [AB].
est un vecteur
unitaire. Notation avec barre de surligement. Le segment étant noté [AB].
Métaheuristique: algorithme
d'optimisation visant des cas difficile à résoudre.
Cas où l'on ne connait pas de méthodes classiques efficaces.
– a. metaheuristic
En
informatique et en optimisation mathématique, une métaheuristique est une
procédure ou une heuristique de niveau supérieur conçue
pour trouver, générer, régler ou sélectionner une heuristique (algorithme de
recherche partielle) qui peut fournir une solution suffisamment bonne à un
problème d'optimisation ou à un problème d'apprentissage automatique, en
particulier avec des informations incomplètes ou imparfaites ou une capacité de
calcul limitée.
Les métaheuristiques sont
généralement des algorithmes stochastiques
itératifs, qui progressent vers un optimum global par échantillonnage d’une
fonction objectif. Elles se comportent comme des algorithmes de recherche,
tentant d’apprendre les caractéristiques d’un problème afin d’en trouver une
approximation de la meilleure solution. (Wikipédia)
Méthode de résolution: comment résoudre
une équation, comment trouver les solutions, les racines.
–
v. Résoudre
une équation
– a. Method fo solving equation, to solve an equation is to find its solutions,
Mètre: unité de mesure
du système international (SI).
– v. Mètre, unité de mesure de
longueur
Mètre carré – v. Are, hectare
Mètre cube – v. Stère
Métrique: graduation
permettant la mesure d'une grandeur.
– ex. Axe muni d'une métrique.
Fonction ou espace métrique: généralisation, notamment en topologie,
de la notion habituelle de distance (longueur du segment entre deux points).
Une métrique est une fonction qui calcule la distance entre
deux points dans l'espace. La fonction génère un nombre réel d(x, y) pour
chaque paire de points. La fonction doit satisfaire certaines propriétés:
![]() symétrie
(valable dans un sens comme dans l'autre,
symétrie
(valable dans un sens comme dans l'autre,
![]() séparation (si d = 0, les points sont confondus),
séparation (si d = 0, les points sont confondus),
![]() inégalité
triangulaire (distance entre deux points plus courte que la somme des
distance de ces points à un troisième).
inégalité
triangulaire (distance entre deux points plus courte que la somme des
distance de ces points à un troisième).
– v. Espace métrique:
distance euclidienne, distance de Manhattan, distance de Minkowski
– a. Metric space: the distance is measured by a function called a metric or
distance function.
Distance ultra-métrique: Voir Ultra-métrique
Mettre en équation: formuler les équations qui traduisent les données
(l'énoncé) d'un problème.
– a. To put in an equation, equate; there is a need to equate performances (il
est nécessaire de mettre les performances en équation).
Micro : facteur
multiplicatif par 1 /1 000 000 = 10 -6
– v. Micro, préfixes (micro,
nano, kilo, méga …)
Milieu
d'un segment: point M situé à égale distance des deux extrémités A et B.
En terme de longueur: MA = MB = ½ AB
– v. Construire
le point milieu, médiane, médiatrice, demi
– a. Midpoint
Théorème des milieux: dans un triangle, la
droite qui passe par le milieu de deux côtés est parallèle au
troisième et réciproquement. La longueur du segment joignant les
deux point est moitié de celle du troisième côté.
– v. Théorème du point milieu
– a. Triangle midpoint theorem: The line segment connecting the midpoints
of two sides of a triangle is parallel
to the third side and is congruent to one half of the third side.
Mille = 1 000 = 103 orthographe: deux mille, deux mille cent vingt.
– v. Mille, kilo; mile, unité de mesure
– a. Thousand, two hundred and fifty thousands (250 000); dans le mile se dit: in the bullseye.
When preceded by a determiner or numeral and followed by of, it can be
singular or plural: two thousand of the inhabitants
Milliard = 1 000 000 000 =
109
– orthographe: deux-milliards, deux-milliards
cent-vingt.
– attention: milliard en anglais se dit billion,
alors que billion en France, c'est 1000 milliards.
– v. Milliard, nom des grands nombres,
giga, zillion
– a. Billion (Attention
!)
Million = 1 000 000 = 106
– orthographe: deux-millions, deux-millions
cent-vingt.
 – v. Million, méga,
préfixes (micro,
nano, kilo, méga …)
– v. Million, méga,
préfixes (micro,
nano, kilo, méga …)
– a. Million
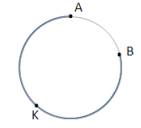
Mineur
(arc - de grand cercle): le plus petit des
deux arcs compris entre deux points donnés d'un cercle.
– a. minor arc
Minimax et maximin**: la valeur la plus
grande possible à un problème de calcul de minimums dans un jeu, un concours,
une compétition, un processus industriel, etc.
C'est la plus grande valeur qu'un joueur peut être sûr d'obtenir connaissant
les actions de son concurrent.
En théorie des jeux ou théorie de la décision, calcul du plus grand minimum de
gain (maximin) ou du plus petit maximum de gain (minimax). Gain est pris au
sens large.
– ex. duel entre tireur de penalty et gardien de but: l'un doit choisir où
diriger son tir, l'autre quel zone à protéger.
– a. Minimax, saddle point
Théorème du minimax ou théorème fondamental des jeux à deux joueurs.
Démontré en 1926 par John von Neumann. Méthode qui permet de prendre une
décision dans le cas d'une compétition entre deux protagonistes comme, par
exemple, deux entreprises concurrentes.
– a. Minimax theorem
Minimum: plus petit élément
d'un ensemble ordonné; la plus petite des valeurs d'une fonction sur un
intervalle donné.
– a. Minimum
Minkowski: espace vectoriel de
dimension 4, muni d'un produit interne (multiplication entre vecteur),
Ce produit interne permet de définir la notion d'orthogonalité.
– v. Distance de Minkowski
– a. Minkowski space
Ce produit interne, interprété comme une
distance, sépare l'espace en deux parties: l'espace des points pour lesquels
une distance existe, et l'espace des points inaccessibles.
Ces derniers, dans le cadre de la relativité restreinte, sont hors
d'atteinte sans dépasser la vitesse de la lumière.
Minorant: valeur inférieure à
celle donnée ou à toutes celles données.
On dit que a est un minorant de A, si tout élément de A est supérieurl à a.
– notation: ![]()
–
cont. Majorant
– a. Upper and lower bounds
Minute de temps: il y a soixante minutes dans une heure. La minute n'est
pas une unité du système SI.
– abréviation: min (et non pas mn et non
plus ' qui est réservé à la minute d'arc).
– v. Minute
– a. The minute is a unit of time usually equal to 1/60 of an hour, or 60
seconds.
– a. Minute hand: aiguille des minutes
Minute d'angle: il y à soixante
minutes dans un degré.
– abréviation par le symbole prime: ' comme
dans 20° 30'
– v. Angles, sexagésimal
– a. A minute of arc or arcminute (arcmin)
Miroir: ustensile utile
pour faire comprendre le principe des symétries;
la réalité est cependant  plus compliqué
qu'il n'y paraît; prenons la main droite: même si elle est placée à gauche de
l'individu dans le miroir c'est toujours la main droite (avec son grain de
beauté, par exemple) mais elle est retournée en 3D comme on retourne un gant
souple; ce phénomène explique très simplement pourquoi nous voyons le même
individu dans le miroir avec ses pieds en bas et sa tête en haut.
plus compliqué
qu'il n'y paraît; prenons la main droite: même si elle est placée à gauche de
l'individu dans le miroir c'est toujours la main droite (avec son grain de
beauté, par exemple) mais elle est retournée en 3D comme on retourne un gant
souple; ce phénomène explique très simplement pourquoi nous voyons le même
individu dans le miroir avec ses pieds en bas et sa tête en haut.
– v. Symétrie
/ Énigme miroir
– a. Mirror
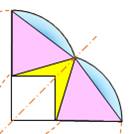
Mixtiligne: qui est formé de
ligne droites et de lignes courbes.
Ex: calculer l'aire de la surface bleue mixtiligne de la figure ci-contre.
– a. Mixtilineal
Mod: abréviation de
modulo
– notation:
![]() qui se lit: 5 est
égal à 1 modulo 2 et qui s'interprète
comme: le reste de la division de 5 par 2 est 1.
qui se lit: 5 est
égal à 1 modulo 2 et qui s'interprète
comme: le reste de la division de 5 par 2 est 1.
– v. Modulo, congruence, résidus.
– v. Modulo, arithmétique
modulaire.
– a. Mod
Modalité: synonyme de valeur
en statistique.
Les modalités xi sont les valeurs prises par un caractère
X.
Les modalités correspondent donc à l'ensemble des valeurs possibles.
– ex: les modalités de
la variable "situation familiale" sont : célibataire, marié, veuf,
divorcé.
– a. Modality: modality signifies whether a
certain data object must participate in the statistics or not. The cardinality is defined as the metric used to specify the number of
occurrences of one object.
Mode: individu le plus
fréquent; en statistique, le mode (ou la classe modale) est la valeur (ou la
classe de valeurs) de X pour laquelle
l'effectif (ou la fréquence) est maximal(e). C'est la donnée la mieux
représentée.
– proche: Médiane, moyenne, paramètres de tendance;
– v. Statistique, vocabulaire
des statistiques
– a. Mode: The element that occurs most frequently in a given set.
Modèle: formulation
mathématique d'un phénomène visant à le reproduire au mieux.
– ex: un modèle de mécanique du vol est
exploité pour réaliser les simulateurs d'entraînement au
pilotage des avions. Les équations et règles mises en place donnent l'illusion
que l'avion est véritablement dans le milieu réel; son comportement est très
réaliste au point que les pilotes, à l'issue de leur entraînement sur
simulateurs, peuvent aller directement aux commandes de l'avion réel.
– ex: les modèles mathématiques en finance servent à mesurer et quantifier
les risques des investissements; ils ont été contestés lors de la grande crise
financière de 2008.
– a. Model
Modulaire
(Arithmétique -): arithmétique qui ne s'intéresse qu'aux restes des divisions.
– v. Modulo, congruence, résidus.
– v. Modulo
– a. Modular arithmetic: modular arithmetic is arithmetic done with a limited
set of numbers. For example, clock arithmetic is an example of modular
arithmetic;
Modulaire (forme ou
fonction -)***: fonction analytique complexe faisant intervenir des fonctions elliptiques (de
Weierstrass).
– note: La nuance entre forme et fonction est
du domaine des experts.
– v. Constante de Ramanujan / Monstre
– a. Modular form
Importance: les formes modulaires
représentent des fonctions génératrices de fonctions arithmétiques. Un exemple
célèbre provient de la preuve de A. Wiles du théorème de Fermat et de la
Conjecture de Taniyama-Weil, où la fonction génératrice est associée au comptage
du nombre de points d’une courbe elliptique sur un corps fini.
Module:
longueur
(r) caractérisant un nombre
complexe en notation polaire, l'angle étant l'argument;
![]()
Parfois utilisé pour la norme d'un vecteur.
– v. Module
d'un nombre complexe, argument, intensité.
– a. Modulus or absolute value
Modulo*
voisin
de "reste dans la division";
– ex: 5 modulo 3 est
égal à 2, noté 5 ![]() 2 mod 3; on dit aussi que 5 et 2 sont congrus modulo 3.
2 mod 3; on dit aussi que 5 et 2 sont congrus modulo 3.
– ex: au lieu de
dire, lorsque 17 est divisé par 4 le reste est égal à 1, on dit 17 est égal à 1 modulo 4 et on note: 17 ![]() 1 mod 4 (ou parfois 17==1 mod 4). On dit
aussi: 17 est congruent à 1 mod 4.
1 mod 4 (ou parfois 17==1 mod 4). On dit
aussi: 17 est congruent à 1 mod 4.
– v. Modulo
et congruence
– a. Modulo. Two integers a and b are said to be congruent modulo n (th modulus), if n
is a divisor of their difference (a − b = kn).
Moebius (ruban de -): ruban qui ne
possède qu'une seule face. Objet unilatère.
– ortho. Moebius,
Möbius, Mobius
– v.
Moebius
– a. Möbius strip, band or loop
Moindres carrés
(méthode des -): elle permet d'ajuster une modèle mathématique à des données
expérimentales; par exemple approximation par une droite moélisant au mieux ces
données.
– v. Régression linéaire
– a. Least square method
Moins (signe -): opérateur de la
soustraction
– v. Soustraction
– Initiation
– a. Minus sign, the substraction operator
Moitié: synonyme de demi, coupé en deux.
– a. Half. Half of ten is five.
MOLS: multi-orthogonal latin
squares, carrés latins mutuellement orthogonaux.
Nombreux
usages, notamment pour coder les messages de sorte que le décodage détecte et
répare des erreurs de transmission.
Moment*
d'ordre
r d'un caractère quantitatif prenant les valeurs x1, x2 …
xn avec une fréquence f1, f2 … fn
est égal à x1r
f1 + x2r f2 + … +
xnr fn
Le moment d'une variable aléatoire est un indicateur de la dispersion de cette
variable.
–
exemple: l'écart
type est la racine carrée du moment centré d’ordre 2.
– v. Espérance
– a. Moment
![]() l’espérance
est
le moment d’ordre un – the first moment is the expected value;
l’espérance
est
le moment d’ordre un – the first moment is the expected value;
![]() la
variance est le moment centré d’ordre deux
– the second central moment is the
variance;
la
variance est le moment centré d’ordre deux
– the second central moment is the
variance;
![]() le
coefficient d’asymétrie est le moment centré réduit d’ordre trois – the
third standardized moment is the skewness;
le
coefficient d’asymétrie est le moment centré réduit d’ordre trois – the
third standardized moment is the skewness;
![]() le
kurtosis non normalisé est le moment centré réduit d’ordre quatre – the fourth
standardized moment is the kurtosis.
le
kurtosis non normalisé est le moment centré réduit d’ordre quatre – the fourth
standardized moment is the kurtosis.
Moment d'inertie: Le moment d’inertie
d’une distribution de masse par rapport à un axe est égal à la somme des
produits de chaque élément de masse mi par le carré de la
distance ri de cet élément à
l’axe: ![]()
Le
moment d'inertie caractérise le comportement d'un système en rotation; le
pendant de la masse pour les translations
– a. Moment of inertia, mass moment of inertia,
angular mass, second moment of mass, or most accurately, rotational inertia,
Monadique: qui n'a qu'un seul
opérande. Relation qui a une arité de 1.
– syn. Unaire.
– v. Numération monadique,
unaire
– a. Monadic
Monienne: étant donnés deux cercles
sécants, une droite passant par l'un des deux points d'intersection est appelée
une monienne. La droite passant par les
deux points est un axe radical (radical axis) et elle est perpendiculaire à
l'axe des centres (line of centers).
Monique (polynôme): coefficient unité
pour le monôme de plus haut degré d'un polynôme à une seule variable.
– syn. Unaire.
– v. unaire
– a. Monic
Monogène: ensemble qui
possède un élément générateur.
Il existe un élément a, le générateur du groupe, tel que tout élément du
groupe puisse s'exprimer sous forme d'un multiple de a.
– v. Groupe cyclique.
– a. Cyclic group or monogenous group: that is generated by a single element.
Monohédral (pavage -): découpe d'une
surface plane en parties congruences (égales).
– v. Pavage monohédral du
disque
– a. Monohedral disk tiling
Monoïde**: structure
algébrique.
Ensemble
muni d'une loi de
composition interne associative et d'un élément neutre.
– v. Vocabulaire des structures algébriques
– a. Monoid: a set with an associative binary operation and an identity
element.
Monôme: polynôme à un seul
terme (a, 6a², - 17a5 ).
– v. Polynôme, binôme, trinôme
– a. Monomial: a polynomial expression consisting of only one term.
Monotone: synonyme de croissante ou décroissante
– a. Monotonic fucntion or monotone function
Monstre (groupe -): groupe qui possède
davantage d'éléments que le nombre d'atomes de la planète Terre (8,08 1053).
Groupe sporadique le plus gros dont l'existence a été
conjecturée bien avant sa construction.
–
v. Groupe monstre
– a. Monster group, Fischer–Griess monster, the friendly giant
Monte-Carlo
(méthode -) production de séquences aléatoires pour calculer les valeurs numériques
(techniques probabilistes).
Production algorithmique de
scénarios au hasard avec pour but de se rapprocher d'une solution.
– histo. Méthode mise au point par Nicholas Metropolis en 1947. Allusion à
Monte Carlo (près de Monaco), ville réputée pour ses jeux de hasard.
– v. Jeu de GO / Jeu de Poker
– a. Monte Carlo method or Monte Carlo experiment
Motif: élément de base et
répétitif dans un dessin, un ensemble.
– v. Frises
– a. Pattern
Montrer: veut dire démontrer,
prouver d'une manière évidente et convaincante.
– v. Démonstrations
– a. Show, prove, demontrate

Morgan (Théorème ou loi
de De -): en logique:
Le NON d'un OU est identique au ET des NON de chaque variable et
Le NON d'un ET est identique au OU des NNON de chaque variable.
– v. Théorème de De Morgan, lois
de De Morgan
– a. De Morgan's laws: the rules can be expressed in English as:
the negation of a disjunction is the conjunction of the negations and
the negation of a conjunction is the disjunction of the negations.
Morphisme
ou homomorphisme: transformation particulière d'un ensemble en un autre.
Notion fondamentale permettant de comparer et de relier des objets
mathématiques entre eux.
Application entre deux ensembles munis d’une même espèce de structure, qui
respecte cette structure.
Application f d'un ensemble E (muni de l'opération ![]() ) dans un ensemble E' (muni de l'opération
) dans un ensemble E' (muni de l'opération ![]() ), telle que
), telle que ![]() pour tout couple (x, y) d'éléments
de E.
pour tout couple (x, y) d'éléments
de E.
– v. Morphismes, application, vocabulaire des structures
algébriques
– a. Morphism: a structure-preserving map from one mathematical structure to
another one of the same type.
Le morphisme est présent dans de nombreux domaines mathématiques.
![]() théorie
des ensembles: les morphismes sont des fonctions ;
théorie
des ensembles: les morphismes sont des fonctions ;
![]() algèbre
linéaire: des transformations linéaires ;
algèbre
linéaire: des transformations linéaires ;
![]() théorie
des groupes: des homomorphismes de groupes ;
théorie
des groupes: des homomorphismes de groupes ;
![]() topologie:
des fonctions continues, etc.
topologie:
des fonctions continues, etc.
Mouvement: déplacements d'un
corps dans l'espace.
Mouvement uniforme: qui s'effectue
régulièrement, à vitesse
constante; ex: voiture sur autoroute; caractérisé par une équation du premier degré.
– v. Force
– a. Uniform motion
Mouvement accéléré: dont la vitesse
augmente; ex: un objet qui tombe; caractérisé par une équation du second
degré.
– v. Force
– a. Accelerated motion
Moyenne
arithmétique: idée de partage équitable; j'ai 20€, tu en as 10 soit un total de 30 à
nous deux, c'est comme si on avait 15€ chacun si on partageait; la moyenne de n
nombres est égale à leur somme divisée par n.
– v. Moyenne
arithmétique / Les
Moyennes (une introduction)
– a. Arithmetic mean (or average)
Moyenne d'une série statistique : représente le caractère moyen.
C'est la moyenne arithmétique des caractères (longueur, salaire …).
– ex. Trois individus de 1,70m, 1,73m et
1,92 m, la moyenne est 1,78 m (somme des 3 valeurs divisée par 3).
Ne pas confondre moyenne, médiane et
mode.
– v. Statistique, paramètres de tendance, vocabulaire
des statistiques
Moyenne pondérée: la moyenne d'un certain
nombre de valeurs affectées de coefficients.
– ex. le cas classique est celui de ma
note moyenne en classe: 16 en maths coef 4, 8 en français coef 2 et 12 en gym
coef 1: moyenne pondérée = 16x4 + 8x2 + 12x1 / (4+2+1) = 92//7 = 13,1.
C'est la somme
des nombres, chacun multiplié par son coefficient de
pondération, le tout, divisé
par la somme des coefficients.
– v. Coefficient de proportionnalité
– a. Weighted arithmetic mean
Moyenne géométrique: pour deux valeurs, racine carrée de
leur produit.
Pour n valeurs racine nième de leur produit.
– note: la moyenne géométrique utilise le produit, alors que la moyenne
arithmétique utilise la somme.
– v. Moyenne
géométrique / Moyenne arithmético-géométrique
– a. Geometric mean (or average)
Moyenne quadratique*: racine carrée de
la moyenne arithmétique des carrés des
valeurs.
– v. Moyenne quadratique
– a. Root mean square (RMS) ot quadratic mean
Moyenne harmonique* telle que 2/M = 1/a
+ 1/b >>>
– v. Moyenne
harmonique
Moyenne
proportionnelle: synonyme de moyenne géométrique.
– ex. Dans 4 / x = x / 25, x est la
moyenne proportionnelle et vaut x² = 4 x 25 = 100 et x = 10.
– a. Mean proportion.
MSO***: modélisation-simulation-optimisation
qui repose surtout sur les équations aux dérivées
partielles. Cette discipline mathématique permet de modéliser des
phénomènes particulièrement sensibles telles la propagation des fissures dans
les cuves réfrigérantes des centrales nucléaires ou dans les
ailes d'avion en matériaux composites,
ou bien encore la discrétion acoustique
des sous-marins nucléaires.
– a. Modeling-simulation-optimization
Multiensemble: il peut comporter
plusieurs exemplaires d'un élément, alors que l'ensemble n'a qu'un exemplaire
unique.
– inform. un ensemble ne comporte qu'un exemplaires des éléments et ordonné {1,
6,7,9}, alors qu'une liste compote des répétitions et un ordre [6, 1, 1, 7,6]
– v. Ensemble / Multiensemble / Programmation listes et
ensembles
– a. Multiset, bag
Multinôme (formule du
-):
utilisée pour le développement d'un polynôme élevé à une puissance. Avec une
élévation au carré, il s'agit de la formule du binôme.
– v. Coefficients multinomiaux
– a. Multinomial theorem: It is the generalization of the binomial theorem from
binomials to multinomials.
Multiple d'un nombre: tous les produits de ce
nombre par un autre. ex: 6, 12, 18, 24 …
– v. Multiples
Sous-multiple: le nombre 4
contenu un nombre de fois entier dans 12 est un sous-multiple de 12.
Aussi, division par 10,
100 … des unités
de mesure.
– ex. le millimètre est un sous-multiple du mètre.
– v. Plus petit multiple commun (PPCM).
– a. Multiple: for example, 14 is a multiple of 7.
Multiplicande: dans 3 x 6, le 3
est le multiplicande et 6 est le multiplicateur.
– v. Multiplicande
– a. Multiplicand
Multiplicateur: dans 3 x 6, le 3
est le multiplicande et 6 est le multiplicateur.
– v. Multiplicateur
– a. Multiplier
Multiplication:
multiplier
a par b c'est ajouter b fois le nombre a; opération notée x entre deux nombres
(3 x 4), notée par un point ou rien entre deux lettres (a.b ou ab).
– v. Multiplication, notation (symbole) de la
multiplication, vocabulaire
des structures algébriques
– a. Multiplication
Multiplication (tables de -)
–
v. Tables de multiplication
faciles
– a. Multiplication tables
Multiplication des nombres
relatifs: deux mêmes signes donnent plus
et deux signes contraires donnent moins.
– ex: 3 (5 -4) = 15 – 12 = 3 et (-3) (5 -4) = (-15) + 12 = -3
– v. Nombres relatifs
/ Règle des signes
Multiplication des fractions: le numérateur
est le produit des numérateurs et le dénominateur
celui des dénominateurs;
– ex: ![]()
– v. Fraction – Exemples
de calculs
– a. Multiplication of fractions, multiplying a fraction by another
fraction.
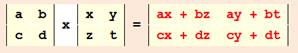 Multiplication de deux matrices: c'est une matrice
carrée résultant de la composition de deux matrices compatibles: l'une a une
quantité de colonnes égale à la quantité de lignes de l'autre.
Multiplication de deux matrices: c'est une matrice
carrée résultant de la composition de deux matrices compatibles: l'une a une
quantité de colonnes égale à la quantité de lignes de l'autre.
– v. Multiplication
de matrices
Mutatis mutandis: En changeant ce qui
doit être changé.
En remplaçant ceci par cela.
Ce qui devait être changé ayant été changé.
Une fois effectués les changements nécessaires.
Mutuellement exclusif: Des évènements
sont mutuellement exclusifs s'ils ne peuvent pas se produire en même temps.
Lorsque deux évènements sont mutuellement exclusifs, l'ensemble-solution de
leur intersection est: A ∩ B = ∅ .
–
v. OU exclusif
– a. Mutually exclusive
![]()
|
Voir |
|
|
Aussi |
|
|
Autres |
|
|
Cette page |
![]()


