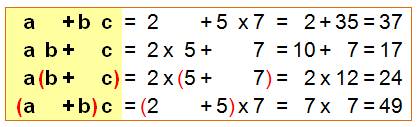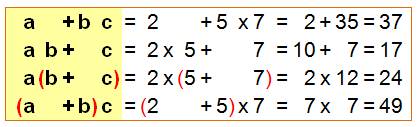9 NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/02/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ALGÈBRE
Débutants Algèbre	BASES				Glossaire Algèbre
INDEX Équations Arithmétique et Algèbre	Techniques de base		Additions	Multiplications
	Parenthèses		Multi Parenthèses	Tracas classiques
	Relations de Viète
	Collèges	Sommaire de cette page >>> Polynôme >>> Produit >>> Puissance >>> Méthode >>> Réduire une expression >>> Développer une expression >>> Factoriser ne expression

Techniques de base de l'algèbre

Vocabulaire de l'algèbre,

Expressions algébriques,

Simplification.

Que vaut l'inconnue notée X ? Voir Chiffres romains / Brève 643

Devinette simple en guise d'amuse-bouche Résoudre: a + b = 200 a – b = 100 Valeur de: a / b = ? Solution

Simple exercice pour se lancer : a + b = 20 et a – b = 10

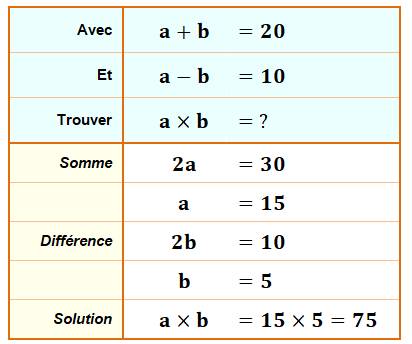
Exemple de réponse que vous trouverez sur cette page

Question

Comment calcule-t-on a + b c en l'absence de parenthèses?

Réponse

a + b c = a + (b c)

La multiplication est prioritaire.

On la calcule en premier, comme s'il y avait des parenthèses.

Exemples

3 + 4 5 = 3 + 20 = 23

3 x 4 + 8 9 = 12 + 72 = 84

Et aussi

Même chose pour la division

a + b / c = a + (b / c)

Exemple

3 + 20 / 4 = 3 + 5 = 8

Voir Exemples de cas ambigus (qui affolent le Net)

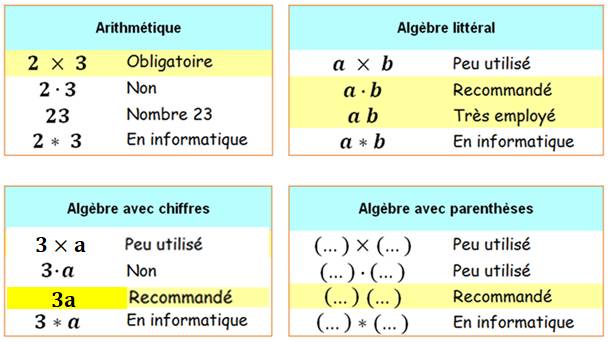
Attention à la notation de la multiplication

Trois possibilités: X pour les nombres et pour débuter en algèbre.
Le point est habituellement utilisé en algèbre (calcul avec des lettres à la place des nombres). Le point disparait lorsqu'il n'y a pas de confusion possible. >>>

Merci Corine

Suite >>>

Vocabulaire

Voir DicoMots des Maths

Polynôme et expression algébrique

Rigoureusement, un polynôme est de la forme:

P = a₀ + a₁x + a₂x² + a₃x³ + …

Sinon, comme ci-dessus, on parle plutôt d'expression algébrique.

Voir Vocabulaire du calcul des expressions algébriques

POLYNÔME
ALGÈBRE L'algèbre traite des données comme en arithmétique, mais sur un plan plus général. POLYNÔME ou EXPRESSION ALGÉBRIQUE Suite de symboles Formant des termes Chacun étant séparé par le signe + ou – L'ordre des termes n'a pas d'importance: 4a + 5b = 5b + 4a	En arithmétique, on utilise des nombres. En algèbre, on utilise des symboles. Les symboles utilisés sont des lettres. Certains usages sont à respecter. x, y, z sont des inconnues; a, b, c sont des coefficients sensés être définis; k, h sont des coefficients multiplicatifs; n, m sont utilisés pour les puissances. Une lettre conserve la même valeur tout au long du même travail.
	4a + 5b + 6c + 2x + 125y est un polynôme de 5 termes 4a est un monôme 4a + 5 b est un binôme 4a + 5b + 6c est un trinôme Note: Le terme polynôme est plutôt réservé aux expressions en x^n.
	Anglais Algebra Algebraical expression Term	Simple expression Binomial expression Trinomial expression Multinomial expression

Voir Définition des domaines mathématiques / Origine des notations

PRODUIT
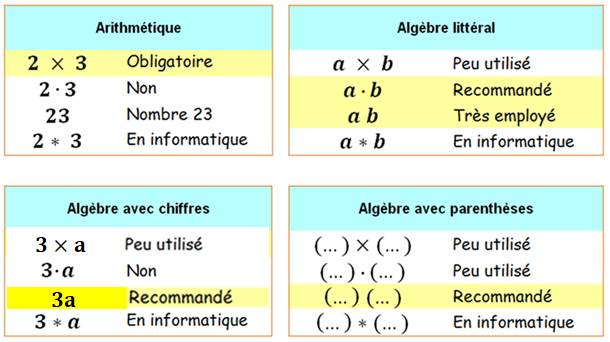
Deux quantités multipliées forment un produit. Chaque quantité multipliée est appelée facteur. Si un seul des facteurs vaut zéro, le produit est nul.	En arithmétique, le produit s'écrit: 3 x 5 Il n'y pas de confusion possible avec la lettre x. En algèbre, il y a plusieurs possibilités. Ce tableau montre les différentes possibilités.
Notez: Le signe de multiplication n'est pas le X mais le caractère × dont le code hexadécimal est 00D7 Le point de la multiplication est le point médian (au milieu de la ligne). Code: 00B7. Le point de ponctuation est utilisé par les Anglo-Saxons à la place de notre virgule. Chez eux, on peut trouver une opération comme celle-ci: Vous trouverez les symboles de la multiplication en faisant insérer/symbole:
Le facteur numérique est appelé le coefficient. Si le coefficient est 1, il est sous-entendu. Parfois, le mot coefficient est utilisé pour une expression littérale (une lettre). L'ordre des facteurs n'a pas d'importance (commutativité): 5 x 3 = 3 x 5 et ab = ba On prend néanmoins l'habitude de les ranger par ordre alphabétique pour mieux s'y retrouver.	Attention En arithmétique 35 = 3 x 10 + 5 En algèbre ab est un produit: si a = 3 et b = 5 alors ab = 3 x 5 = 15 et 35ab = 35 x 3 x 5 = 525 Facteurs et coefficients 5abc est un produit de 4 facteurs, 5 est le coefficient de abc, 5a est le coefficient de bc.

Voir Notations de la division / Priorité des opérations

Le produit est prioritaire sur la somme Comme en arithmétique: Le résultat d'une addition est une somme; et celui de la multiplication est un produit. Le produit est "plus fort (prioritaire)" que la somme: Le produit est effectué en premier et les sommes ensuite. Modifier cet ordre, exige l'emploi de parenthèses: La parenthèse doit être considérée comme un lieu d'intimité. Il faut y exécuter les opérations en priorité.

Somme de deux termes: a + b Produit de deux facteurs: a.b Attention Ne pas confondre somme et produit si a = 5 et b = 7 alors: a + b = 5 + 7 = 12 a . b = 5 x 7 = 35 Exemples Si a = 2, b = 5, c = 7 alors:

Anglais: Product, factor, coefficient, literal coefficient

PUISSANCE
Si une même donnée est multipliée par elle-même un certain nombre de fois c'est une puissance. Le nombre de fois est appelé l'exposant. L'exposant 1 est sous-entendu. Toute puissance de 1 est égale à 1. Toute puissance de 0 est égale à 0. Les facteurs d'un produit peuvent être chacun élevés à des puissances différentes.	a . a = a puissance 2, notée a^2 ; 2 est l'exposant. a . a . a = a puissance 3, notée a^3 ; 3 est l'exposant. a = a puissance 1, notée a^1ou simplement a.
	Piège: ne pas confondre 3a qui veut dire 3 fois a soit a + a + a a^3 qui veut dire a puissance 3 soit a . a . a Exemple: si a vaut 5 3a = 3 x 5 = 15 a^3 = 5^3 = 5 x 5 x 5 = 125 et 5a + a^3 – 6a^2 = 5 x 5 + 5^3 – 6 x 5^2 = 25 + 125 – 150 = 0
	a^3. b^6. c^2 = a.a.a.b.b.b.b.b.b.c.c

Anglais

Power a² : Second power of a a^3 : Third power of a a^4 : Fourth power of a

Index or exponent a² : a squared a^3 : a cubed a^4 : a to the fourth (power)

MÉTHODE – Rigueur

Il faut s'habituer à travailler proprement et toujours de la même manière

Adopter les règles indiquées ci-dessus;

Ordre alphabétique pour les termes;

Les termes semblables proches;

Et l'un sous l'autre dans le cas des opérations.

Exemples

Ordre par puissances décroissantes, du premier facteur littéral.

5a^5b^3c

+ 2a^4b^3c

+ 10a^3bc

+ 3a^2bc^2

+ abc

Somme de deux polynômes

	4a	+ 5b	– 6c	+ 17d
+	a	– 3b	+ 6c	+ 3d
=	5a	+ 2b		+ 20d

Réduire une expression
Il s'agit de regrouper les termes de même nature. L'usage veut que les plus grands exposants de x soient en tête.	3 + 4x + x² + 2 – 2x – 2 + 5x² = 6x² + 2x + 3 x^2 + 2x^3 + 5x^7 + 2x^2 + 2 = 5x^7 + 2x^3 + 3x^2 + 2 6 + xy + x²y + 10yx + 3xy² = x²y + 11xy + 3xy² + 6

Développer une expression
Il s'agit d'éliminer les parenthèses et les facteurs communs	2(x + 2) = 2x + 4 2(x + 2) x = 2x² + 4x (x + 2) (x – 2) = x² – 4 (x + 2)² = x² + 4x + 4 (x + 2) (x + 3) = x² + 2x + 3x + 6 = x² + 5x + 6

Voir Identités remarquables / Parenthèses

Trois méthodes pour développer une expression à parenthèses

Voir Brève 57-1121

Factoriser une expression
Il s'agit de rendre une expression plus compacte en trouvant des facteurs communs. Opération contraire du développement.	15x + 20 = 5(3x + 4) 15x + 20 + (x + 2)(3x + 4) = 5(3x + 4) + (x + 2)(3x + 4) = (5 + x + 2) (3x + 4) = (x + 7)(3x + 4) 25x² + 70x + 49 = (5x + 7)² 4x² – 49 = (2x + 7) (2x – 7) 3x² + 10x + 8 = 3x² + 4x + 6x + 8 = x(3x + 4) + 2(3x + 4) = (x + 2) (3x + 4)

Cas expliqué, pour tout à fait débutant Comment arrive-t-on à cette factorisation?	25x² + 70x + 49 = (5x + 7)²
On remarque deux carrés aux extrémités	25x², le carré de 5x 49, le carré de 7
On essaie la mise au carré de leur somme	(5x + 7)² = (5x + 7) (5x + 7)
On multiplie chaque terme de l'un par chaque terme de l'autre (On utilise le point pour multiplier, pour éviter la confusion avec x)	(5x + 7) (5x + 7) = 5x . 5x + 5x . 7 + 7 . 5x + 7 . 7
On calcule	= 25x² + 35x + 35x + 49
Nous avons bien nos deux termes extrêmes	= 25x² + 35x + 35x + 49
Quant au milieu, en sommant cela donne 70	= 25x² + 70x + 49

Cas expliqué, pour habitués Nous avons l'idée d'une identité remarquable	(a + b)² = a² + 2ab + b²
En prenant a = 5 et b = 7, le terme central sera 2ab	2ab = 2 . 5 . 7 = 70
Nous sommes sur la bonne piste	(5x + 7)² = 25x² + 70x + 49

Autre exemple expliqué La somme des coefficients des puissances paires est égale à celle des coefficients impairs. Une racine pourrait être -1 et un des facteurs serait: x + 1. La valeur de K se trouve en divisant le polynôme. Rien de plus difficile qu'une division ordinaire. Dans K: 5 est la somme et 6 le produit de deux nombres: sans nul doute 2 et 3.

P = x^3 + 6x^2 + 11x + 6 = ? Factorisez (–1)^3 + 6(–1)^2 + 11(–1) + 6 = 0 Effectivement P = x^3 + 6x^2 + 11x + 6 = (x + 1) K P = (x + 1) (x² + 5x + 6) P = (x + 1) (x + 2) (x + 3) Rappel: (x + a) (x + b) = x² + (a + b) x + a.b

Énigme – Résoudre cette équation avec des racines à étage

-Voir Racines continues / Brève 47-934

Suite	Additions Parenthèses Un exercice d'approche des dérivées Tracas classiques de calculs
Voir	Algèbre – Définition Débutants – Index Dérivées des polynômes Équation avec 3 inconnues et degrés 2, 3 et 4 Équations Équations – Débutant Équations – Glossaire Équations en 1/x Équations énigmatiques – Index Opérations arithmétiques – Initiations Réduction des termes d'une équation Spectre numérique- Exemple de calcul
Cette page	http://villemin.gerard.free.fr/ThNbDemo/EqaBase.htm

Solution

Résoudre: a + b = 200

a – b = 100

a / b = ?

Solution

Autre exemple

Retour / Autres énigmes / Énigmes virales sur le Net