|
||||||||||||||||||||||||||||||||

![]()
|
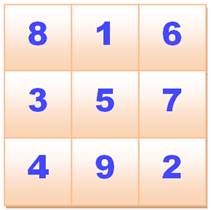
CARRÉS MAGIQUES Spécial débutants / novices Pourquoi le carré magique de 3 x 3 existe-t-il ?
Mais, est-il si magique que cela ? Oui ! Notez bien qu'il existe plus simple que les carrés magiques; ces sont les carrés latins. Le fameux jeu de Sudoku dérive des ces types de carrés. |
Anglais: Magic squares for beginners, for dummies (pour les
nuls)
|
|
||
|
|
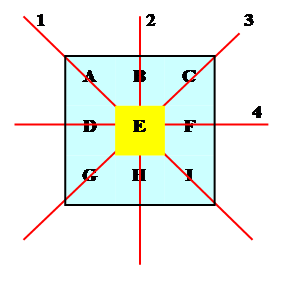
Lignes A +
B + C
= N D +
E + F
= N G +
H + I
= N Colonnes A +
D + G
= N B +
E + H
= N C +
F + I
= N Diagonales A
+ E +
I = N C
+ E + G
= N |
|
Voir Jeux des cryptogrammes / Tous les chiffres de 1 à 9
|
|
||
|
|
A
+ B + C + D + E + F + G + H + I = 1
+ 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 |
|
|
|
A + B + C = N D + E + F = N G + H + I = N |
|
|
|
A
+ B + C + D + E + F + G + H + I = 3N |
|
|
|
3N |
|
|
|
1
+ 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 =
45 |
|
|
|
3N =
45 |
|
|
|
N = 15 |
|
|
|
||
|
|
1 + 5 + 9 = 15 1 + 6 + 8 = 15 2 + 4 + 9 = 15 2 + 5 + 8 = 15 2 + 6 + 7 = 15 3 + 4 + 8 = 15 3 + 5 + 7 = 15 4 + 5 + 6 = 15 4 fois pour le 5 3 fois pour 2, 4, 6, 8 (pairs) 2 fois pour 1, 3, 5, 7 (impairs) |
|
|
|
||
|
|
|
|
|
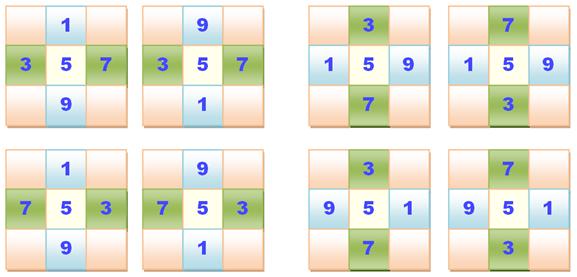
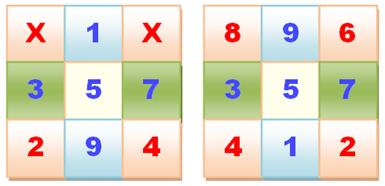
Les
huit façons de positionner les nombres impairs
|
Voir Formule
générique des carrés 3 x 3 / Exercice
de programmation
|
|
||
|
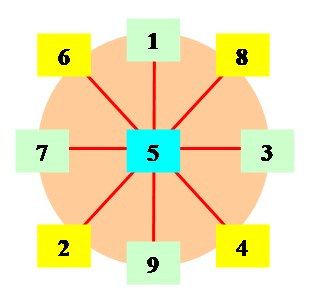
1 2 3 4 5 6 7 8 9
1 = 5 – 4 et 5 + 4 = 9 2 = 5 – 3 et 5 + 3 = 8 3
=
5 – 2 et 5 + 2 = 7
|
|
|
|
|
|
|
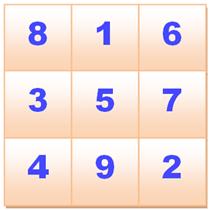
Il existe un carré magique 3 x 3, mais un seul.
Digipartition
et carré magique |
|
|
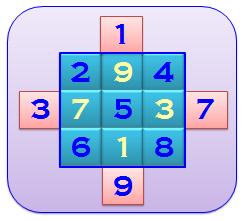
Chaque
cellule du milieu (chiffre blanc) est dépliée sur le milieu opposé (en rose).
Alors les nombres de 1 à 9 (en bleu) apparaissent sur des diagonales, à la
suite les uns des autres. C'est
précisément une des méthodes de construction
du carré magique. |
Notez que le
nombre 7 prendrait sa place naturellement de l'autre côté si le carré était enroulé en cylindre. Et cela est vrai pour
les quatre nombres qui débordent. |
|
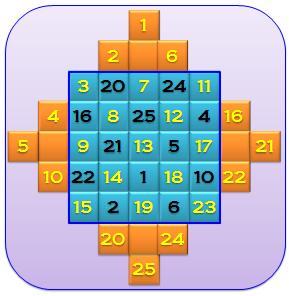
Lançons-nous
et utilisons cette méthode pour construire notre premier carré magique avec 5 x 5 cases. Les nombres à placer vont de 1 à 25 et
la somme magique est 65. La
case centrale est 13 et tous les couples opposés par rapport à cette case
centrale donnent une somme égale à 2 x 13 = 26. Vous
pouvez poursuivre avec des carrés n x n, pourvu que n soit impair. |
Les nombres de
1 à 25 sont placés à la suite les uns des autres, le long des diagonales. Ceux qui débordent
sont "enroulés" de l'autre côté. |
Voir Construction du carré magique 13x13
|
Idée originale: représenter les nombres d'un
carré magique 3x3 par la taille des clés à pipe disposées sur un présentoir à
outils.
Nombres de 8 à
16 pour une
constante magique de 36. Il s'agit d'un carré magique classique dont
chacun des nombres a été augmenté de 7. Cela, pour se retrouver dans une
gamme de clés existantes. |
|
Merci à Gérard Bakner le créateur de ce carré
magique concret
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Sites |
|
|
Cette page |
![]()