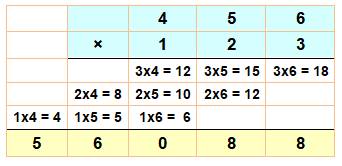![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page For
this page, refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
MULTIPLICATION économe des grands nombres Algorithme
de Karatsuba Comment réaliser une multiplication
avec de grands nombres le plus
rapidement possibles avec un ordinateur.
Quels sont les algorithmes ?
Point des recherches sur ce sujet. En 2019, une avancée théorique
importante a été réalisée. |

|
|
||
|
Quantité d'opérations élémentaires Une
multiplication de deux nombres de trois chiffres nécessite 3 x 3 = 9
multiplications et 4 ou 5 additions. D'une
manière générale une multiplication de deux nombres de n chiffres nécessite n² multiplications. Est-il
possible de réduire la quantité de ces multiplications ? Oui ! |
Un exemple de multiplication
Important: en calcul sur ordinateur, l'addition est simple et peu coûteuse; ce
n'est pas le cas de la multiplication.
D'où la recherche pour en minimiser la quantité. |
|
Voir Multiplication
posée
|
|
||
|
Idée de calculs itératifs Prenons
un exemple avec la multiplication de deux nombres de quatre chiffres. Le
principe consiste à partager chaque nombre de quatre chiffres en deux nombres
de deux chiffres. Le produit
est donné par la formule indiquée. Il suffit
alors d'appliquer cette formule à chacun des sous-produits de deux chiffres
pour arriver à la multiplication de nombres à un seul chiffre. |
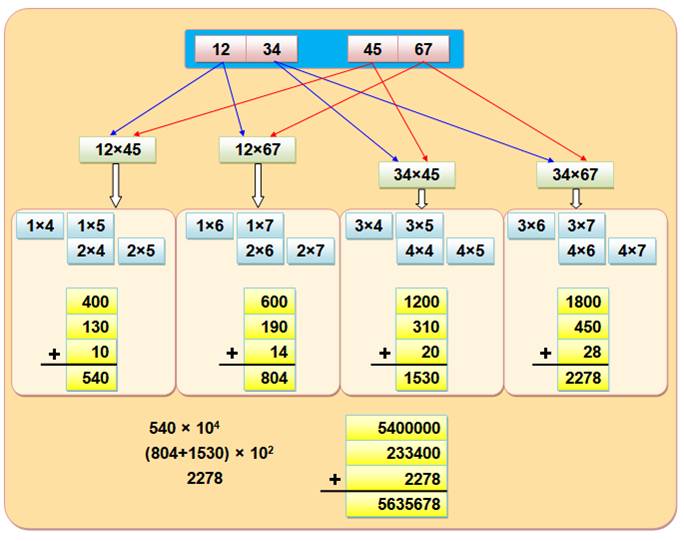
Ex: 1 234 x 4 567 = 12 x 45 x 104 + (12 x 67 + 34 x 45) x 102 + 34 x 67 = 5 635 678 |
|
|
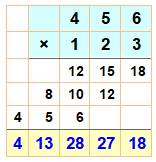
Les 16 multiplications élémentaires
pour deux nombres de quatre chiffres
|
||
|
|
||
|
Cette
méthode reprend la méthode classique en arrangeant les termes de façon
astucieuse, conduisant à trois multiplications élémentaires au lieu de
quatre.
|
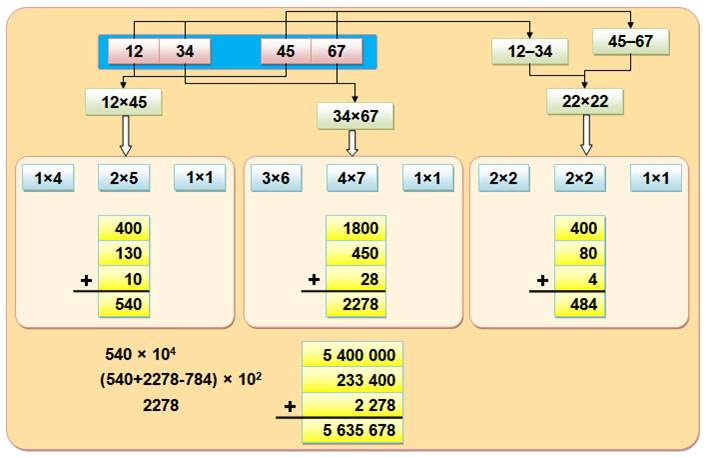
Ex: 1 234 x 4 567 = 12 x 45 x 104 + (12 x 45 + 34 x 67 – (12 – 34) (45 – 67)) x 102 + 34 x 67 = 5 635 678 |
|
|
Seulement 9 multiplications
élémentaires pour deux nombres de quatre chiffres
|
||
|
|
|||
|
Algorithme
qui partage les opérandes en k éléments et les place comme coefficients de
polynômes. Le but
est de retrouver les coefficients par résolution d'équations. |
Exemple (simple!) 56 x 23 p(x) = 5x + 6 et qx = 2x + 3 avec x = 10 r(x) = p(x) q(x) = ax² + bx + c Évidemment on peut calculer le produit du polynôme: r(x) = 10x² + 27x
+ 18 et donner le résultat de la multiplication: 10x100 + 27x10 + 18 = 1288 Avec de grands nombres, une autre méthode est plus économique: calcul
des coefficients en résolvant un système d'équations, et
cela, en choisissant des valeurs de x conduisant à des calculs simples. |
||
|
Ici, on a formé un système d'équations en donnant les valeurs 0, 1 et
-1 à x. |
Implémentation de l'exemple avec la méthode
Toom-Cook
|
||
|
|
||
|
Avec cet
algorithme, on change totalement de monde! Comme souvent en
mathématiques, on transpose le problème dans un autre monde pour utiliser
des outils plus performants et, en fin de calcul, on revient dans le monde
d'origine. |
Une (petite) idée de l'algorithme
Or, la convolution de deux éléments (vecteurs) peut être trouvée en
faisant le produit des FFT* des deux éléments, et en revenant en
arrière en prenant la FFT inverse. (* il s'agit des FFT discrètes,
c'est-à-dire en numérique). |
|
|
|
||
|
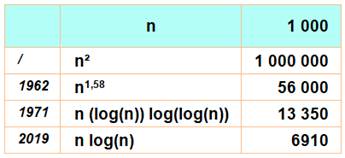
1962, Anatoly
Karatsuba (russe)
1971, Arnold
Schönhage et Volker Strassen (allemands) 2013, Martin Fürer
présente un algorithme dont la performance est en 2log n |
||
|
2019, deux
mathématiciens:
Algorithme
de multiplication qui ne nécessite que n log (n)
multiplications N'est
encore que théorique, mais il pourrait s'avérer d'une grande utilité pour
optimiser la vitesse de calcul des ordinateurs et pour la programmation. Principe: Utilisation
de la transformée de Fourier rapide (FFT). En gros,
la méthode consiste à couper les grands entiers que l'on veut multiplier en
morceaux plus petits de taille environ log n.
Grâce aux propriétés de la FFT, on ramène la multiplication des grands
nombres à des multiplications sur des nombres de taille log n (si n vaut un
milliard, log n est égal à environ 20,7). |
J. van der
Joeven et D. Harvey Cependant cet algorithme n'est intéressant que pour de très, très
grands nombres n > 21729^12 Hoeven cite cet exemple: avec un temps d'exécution d'une multiplication
élémentaire d'une nanoseconde, une multiplication de deux nombres d'un
milliard de chiffres prendrait: (109)² ns = 32 ans L'algorithme connu de Schönhage-Strassen réduit ce temps à une
trentaine de secondes sur un ordinateur ordinaire d'aujourd'hui. Avec le
nouvel algorithme de 2019, la durée serait encore réduite. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()