![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page |
|
22 Novembre 2025
![]()
|
Édition du: 29/11/2025 |
|
INDEX lettre E |
Dictionnaire de base du vocabulaire des mathématiques |
|
|
Faites
un double-clic pour un retour en haut de
page
Pour
trouver un mot: Ctrl F et tapez le mot
cherché
|
Avertissement Dictionnaire pour débutants,
juniors, novices, "nuls" … !!! On privilégie la compréhension par rapport à une rigueur mathématique !!! Les liens permettent de compléter et d'approfondir Pour une
version plus académique se reporter aux ouvrages spécialisés |
Légende Parfois,
plusieurs définitions sont données: de la plus "intuitive" à la
plus correcte mathématiquement Mode de recherche: si vous ne trouvez
pas symétrie centrale à symétrie, voyez à centrale, par exemple. Difficulté: * notion avancée;
** notion complexe. |
![]()
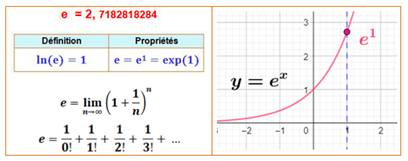 e (exponentielle): constante de Neper ou nombre
d'Euler.
e (exponentielle): constante de Neper ou nombre
d'Euler.
Base des logarithmes
népériens.
Nombre transcendant.
– v. Constante e, fonction exponentielle
– a. e or Euler's number
E retourné:![]() il existe une valeur de x.
il existe une valeur de x.
 – symbole appelé quantificateur existentiel.
– symbole appelé quantificateur existentiel.
– étym. proposé par Peano en 1897
– v. Quantificateurs
– a.
existential quantifier, se dit: all
Ébiseler: donner une forme conique à un trou.
Écart: Différence entre
deux valeurs données, la plus grande moins la plus petite.
– syn. Intervalle,
étendue
Écart: en statistique, l'écart d'une modalité xi
par rapport à un réel
a est le réel positif |xi - a|
(les barres verticales signifient valeur absolue).
– v. Vocabulaire
des statistiques
– a. absolute deviation
Écart à la moyenne: écart entre l'une des valeurs et la valeur moyenne
de l'échantillon.
– ex. La moyenne des salaires
est 1500 euros; il gagne 1450 euros; l'écart à la moyenne est 50 euros.
Écart-moyen*: moyenne
des écarts par rapport à la moyenne.
– a. average deviation
Écart-type* racine carrée de la variance.
Caractérise la dispersion autour de la moyenne.
Plus l'écart-type est grand plus la dispersion est grande.
– v. Statistique, volatilité, paramètre de dispersion
– a. Standard deviation, root
mean square deviation, root mean square error
Échantillon: en statistique,
la partie sur laquelle porte l'étude.
– ex. 3 personnes mesurent 1,73 m sur un échantillon
de 20 personnes.
– v. Statistique,caractère,
population
– a. Sample, random sample
Échantillon représentatif: partie d'un
ensemble respectant toutes les propriétés de l'ensemble.
– a. Representative sample
Échantillonner: en traitement du signal, couper un signal continu
en petites tranches temporelles de façon à pouvoir donner une valeur binaire à
chaque échantillon et, ainsi permettre leur traitement par ordinateur
– v. Shannon et Nyquist, numériser, discret
– a. Sampling
![]() Échelle: l'échelle est un
coefficient de proportionnalité.
Échelle: l'échelle est un
coefficient de proportionnalité.
Elle indique de combien la figure a été réduite (ou agrandie) pour être
représentée.
Échelle = dimension sur la reproduction divisée par dimension réelle
correspondante;
L'échelle e est un nombre positif.
![]() si e = 1,
il s'agit d'une reproduction à taille réelle.
si e = 1,
il s'agit d'une reproduction à taille réelle.
![]() si e > 1,
c'est un agrandissement.
si e > 1,
c'est un agrandissement.
![]() si e < 1,
c'est une réduction
si e < 1,
c'est une réduction
– ex. Pour une carte géographique ou routière au 1
/100 000 (un cent-millième), cela veut dire que 1 cm de la carte représente 100
000 cm de la réalité, soit 1 km
 – v. Homothétie
– v. Homothétie
– a. Scale, the scale of a map
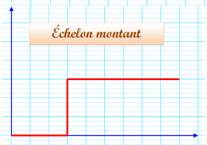
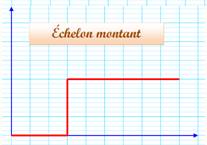
Échelon (fonction - ): la fonction échelon
s'appelle aussi: échelon unité, marche d'escalier ou fonction d'Heaviside,
abrégée en fonction H.
– v. Courbes usuelles
– a. Heavides step function or unit step function.
Éclimètre:
du
latin incliné.
Il permet la mesure des angles verticaux (angles dans le plan vertical),
c'est-à-dire la différence de niveau entre deux points.
Il comporte une lunette mobile dans le plan vertical équipée d'une boussole et
d'un niveau.
– syn. Lunette
topographique, théodolite (général), goniomètre (angles
horizontaux).
Trois types d'angles verticaux pour les géomètres:
![]() Site d ́une visée:
l’angle de la visée avec l ́horizontale;
Site d ́une visée:
l’angle de la visée avec l ́horizontale;
![]() Distance zénithale:
l'angle de la visée verticale ascendante; et
Distance zénithale:
l'angle de la visée verticale ascendante; et
![]() Distance nadirale:
l'angle de la visée verticale descendante.
Distance nadirale:
l'angle de la visée verticale descendante.
– v. Angles verticaux en géométrie.
– a. Eclimeter: An
instrument to be held in the hand for measuring the zenith distances of objects
near the horizon.
Écriture décimale
(conversion décimale): passage d'une fraction à un nombre, en général, en
effectuant la division.
– ex. 1, 714 est l'écriture décimale de la fraction ![]()
– v. Décimale,
virgule, division posée
– a. Fraction to decimal conversion
Écriture fractionnaire: nombre décrit par
une fraction comme ![]()
– v. Fraction
– a. Fractional writting
ECM**: Elliptic curve
method for integer factorization parfois nommée: Lenstra elliptic curve method.
Méthode inventée en 1985 par H.W. Lenstra Jr. Méthode adaptée à la recherche de facteurs
(disons de 10 à 40 chiffres) dans de très grands nombres.
La méthode GMP-ECM a été développée pour la première fois par Paul Zimmermann.
– v. Nombre de Fermat 12, GMP, courbes
elliptiques
EDP: équation aux dérivées
partielles.
– a. Partial differential
equation (PDE).
Effectif ou fréquence
absolue ou fréquence effective: quantité d'individus considéré dans la
statistique.
– v. Statistique, cumulé
– a. absolute frequency
Fréquence relative ou fréquence: quotient de l'effectif par celui de la
population.
– a. relative frequency, proportional frequency,
Effectuer une opération
ou un calcul: exécuter l'opération, donner le résultat.
– a. Calculate, to perfom a
calcuation
Égal: en algèbre: valeur identique en quantité,
– notation: a = b
– v. Égal, différent
![]() en géométrie, synonyme de
superposable, isométrique,
de même forme, congruent
en géométrie, synonyme de
superposable, isométrique,
de même forme, congruent
![]() en théorie des
ensembles, ensembles ayant les mêmes éléments
en théorie des
ensembles, ensembles ayant les mêmes éléments
– orthographe: 15 multiplié par 4 égale 60.
– a. Equal
Égalité: caractérisé une
situation équilibrée.
Choses équivalentes, identiques.
Même quantité d'éléments dans deux ensembles; ils sont les mêmes.
Deux objets mathématiques a et
b sont égaux si a et b sont deux représentations différentes du même objet.
L’égalité mathématique est, en fait, l’identité.
– Notez que: on ne dit pas que deux figures sont égales; elles sont isométriques (ou équivalentes).
– v. Égalité,
isométrie
– a. Equality
Égalité de Bézout ou identité de
Bézout ou théorème de Bachet-Bézout
a
et b sont étrangers
si et seulement si
il existe u et v tels que au + bv = 1.
– v. Identité de Bézout
– a. Bezout's identity
Égalité vectorielle: deux vecteurs sont
égaux s'ils ont même longueur, même direction et même sens.
Les deux vecteurs représentent le même vecteur par translation.
– v. Vecteur
– a. Equal vector, vector equality: equal magnitude and same direction.
Égalités remarquables: Voir en Identités
remarquables
Égalité des produit en croix: si ![]() alors ad = bc
alors ad = bc
– v. Produit en croix, règle de trois
– a. Cross-multiplication
EGF: exponential
generating function et OGF: ordinary generating function
– v. Génératrice
(fonction -)
Élégant: une démonstration
élégante: simple, claire, belle.
Poincaré disait: Les mathématiciens
attachent une grande importance à l’élégance de leurs méthodes et de leurs
résultats.
Cédric Villani dit: L’élégance
en mathématiques, c’est de trouver quelque chose d’inattendu, qui s’imbrique
bien dans un fil directeur, s’intègre dans le reste en faisant une combinaison
harmonieuse. Face à un océan de possibilités, plutôt que d’aller au hasard,
vous vous laissez guider par ce qui semble la voie la plus belle pour trouver
votre chemin
– v. Démonstration
– a. Smart demonstration, smart
proof
Élément:
chacun
des objets appartenant à un ensemble,
à une collection.
– notation: a Î E qui veut dire:
a est un élément de E, ou a appartient à l'ensemble E
– ex.
"été" est un élément de l'ensemble des saisons.
"pentagone" est un élément de l'ensemble des polygones.
– v. Appartenance
– a. Members or element
Élément neutre: qui ne modifie par
le résultat d'une opération.
0 est l'élément neutre de l'addition.
1 est celui de la multiplication.
– v. Vocabulaire
des structures algébriques
– a. Identity element ot neutral element
Élément absorbant: comme le 0 pour la
multiplication: 0 × a = 0.
C'est un élément a tel que ![]() pour tout x de
l'ensemble.
pour tout x de
l'ensemble.
– v. Vocabulaire
des structures algébriques
– a. Absorbing element
Élément symétrique: élément x' tel
que composé par x, le résultat est l'élément neutre.
– Pour l'addition: -2 est
le symétrique de 2; dans ce cas, il est appelé l'élément opposé.
– Pour la multiplication:
1/2 est le symétrique de 2; dans
ce cas, il est appelé l'élément inverse.
– Pour la fonction f définie
dans ![]() , l'élément
symétrique pour la composition des fonctions est la
fonction réciproque f—1, telle que
, l'élément
symétrique pour la composition des fonctions est la
fonction réciproque f—1, telle que ![]() avec I la relation identique dans
avec I la relation identique dans ![]() .
.
Élément opposé: élément qui ajouté au nombre donne zéro.
– ex. L'opposé de 2 est - 2.
Cas d'un ensemble
E muni d’une loi
interne d’addition associative et commutative,
l’opposé d’un élément x de E est le symétrique (s’il existe) de cet élément, et
il est noté -x.
– a. Additive inverse
Élément inverse: élément qui multiplié par le nombre donne un.
– ex. 3 admet
l'inverse 1/3 dans le monde des nombres réels.
– notation: l'inverse de x est noté 1/x ou x-1.
L'inverse est le nom donné à l'élément symétrique, lorsque la loi est notée
multiplicativement.
Élément inversible: élément qui admet
un inverse.
– a. Multiplicative inverse or
reciprocal
Élément finis (méthode des -): calcul des propriétés continuellement
variable d'un composant (contrainte, pression, température, champs …).
Subdivision en un grand nombre de petits éléments qui pourront être analysés
individuellement à l'aide d'équations bine connues.
– a. Finite element method
(FEM): method for numerically solving differential equations.
Élément d'une matrice: nom donné à chacun
des constituant ligne-colonne de la matrice.
– ex. Dans la matrice ![]() , les éléments de
la matrice sont a, b, c et d.
, les éléments de
la matrice sont a, b, c et d.
– a. The numbers,
symbols, or expressions in the matrix are called its entries or its elements
Élément régulier: avec l'addition si
a + x = a + y alors x = y. On dit que a est un élément régulier à gauche pour l'addition. si x + = y + a alors x = y. L'élément a est régulier
à droite. Si les deux cas coexistent, l'élément est simplement régulier.
Extension à tout type d'opérations, toute loi de
composition interne.
– ex. Dans ℕ, tout élément est régulier
pour l'addition. Pour la multiplication, le nombre 0 n'est régulier ni à droite
ni à gauche.
Élément symétrique: généralise la notion d'opposé
pour l'addition ou d'inverse pour la multiplication.
Si E est un ensemble muni d’une loi de
composition interne notée * pour laquelle il existe un élément neutre e,
l’élément x’ de E est dit symétrique à
gauche de l’élément x de E si
le composé de x’ et x est e : x’ * x = e. Un élément x’ de E est dit
symétrique à droite de x si
le composé de x et x' est e : x * x' = e.
Si la loi * est associative et si x admet un symétrique
x'' à droite, et un symétrique x' à gauche, ces deux éléments sont égaux.
Un élément x’ de E est dit symétrique de l’élément x de E si on a à la fois x’
* x = e et x * x’ = e.
Si la loi * est associative, le symétrique x’ de x est unique, on dit que x et
x’ sont symétriques l’un de l’autre.
Si la loi de composition interne est notée + le symétrique de x, s’il existe,
est noté – x et il est appelé l’opposé de x.
Si la loi est notée ×, le symétrique de x, s’il existe, est noté x-1 ou 1/x et il
est appelé l’inverse de x.
Éléments de symétrie: inventaire des possibilités de symétrie
d'une figure.
– ex. Les éléments de symétrie du carré sont:
quatre axes de symétrie et un centre de symétrie.
Le rectangle ne
possèdent que deux axes de symétrie et un centre de symétrie.
– a. Symmetry element: axis of rotation,
center of symmetry …
 Élévation (angle d'-) ou angle de site: angle exprimant la
hauteur d'un objet par rapport à l'horizon.
Élévation (angle d'-) ou angle de site: angle exprimant la
hauteur d'un objet par rapport à l'horizon.
Angle entre l'horizontale et la ligne de visée d'un objet plus haut que
l'observateur.
– v. Dépression, site
– a. Altitude (astronomy),
elevation or elevation angle
Élévation ou hauteur en balistique: angle entre
l'horizontale et la bouche du canon.
À l'origine indiquait la hauteur à imposer pour un tir au canon.
– a. Elevation (ballistics)
Élever au carré, au
cube, à une puissance: élever 7 au cube, c'est
multiplier 7 trois fois par lui-même
– ex. 73 = 7 x 7 x 7 = 343.
– v. Puissances
– a. to square, to cube, to raise 2 to
the power of 6
Élever une perpendiculaire: synonyme de tracer une perpendiculaire.
– v. Abaisser
– a. Draw or construct a perpendicular line
Ellipse:
courbe en forme
d'ovale.
Courbe
plane dont tous les points sont tels que la somme de leur distance à deux
points fixes appelés foyers
est constante.
La détermination de la longueur des arcs d'ellipse
n'est pas immédiate, elle implique l'utilisation des fonctions elliptiques.
– v. Ellipse,
coniques
– a. Ellipse: a plane curve surrounding two focal
points.
Ellipsoïde: volume engendré par une ellipse en rotation autour d'un de
ses axes.
– v. Ellipsoïde
– a. Ellipsoid
 Elliptique (fonction -)** fonctions en y2
= f(x3).
Elliptique (fonction -)** fonctions en y2
= f(x3).
Elles sont utilisées pour calculer la longueur des arcs
d'ellipse; pour démontrer le théorème de Fermat-Wiles; etc.
– v. Courbes elliptiques, fonctions modulaires
Fonction elliptique de Weierstrass**
équation: y² = x3 + ax + b; c'est la famille de base, car toute fonction
elliptique plus générale peut être exprimée avec de telles fonctions. On note
que l'ellipse ne fait pas partie de cette famille de courbes.
– a. Elliptic function
Une courbe elliptique est une courbe algébrique définie par une
équation de la forme : y² = x³ +
ax + b, où a et b sont des constantes telles que le discriminant Δ
= 4a³ + 27b² soit non nul.
Elle possède une structure de groupe sur ses points, ce qui en fait un outil
fondamental en cryptographie et en théorie des nombres.
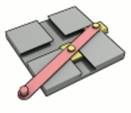
Ellipsographe ou
trammel: instrument articulé qui sert à tracer des ellipses (Illustration).
– v. Construction
des ellipses
– a. Trammel or Archimedes
Émérite
(professeur - ): qui a été professeur et qui, ayant quitté son poste (retraite ou autre),
jouit des honneurs dus à sa notoriété ou ses services.
– ex. Le Pr Ivar Ekeland est professeur émérite à
l’Université Paris-Dauphine.
– a.
University professor emeritus
Empirique: acquis par
l'expérience.
– ex. Connaissances
empiriques.
– a. Empirical
Méthode empirique ou méthode
expérimentale: Recours à des résultats obtenus par l'expérience, par l'observation. Par
opposition aux méthodes analytiques basées sur la résolution d'équations bien
connues.
– v. Méthode analytique
Empirical
method
Empirisme: pensée datant d'Aristote
qui dit que les objets mathématiques préexistent. les mathématiciens ne font
que les dévoiler.
Enantiomorphes:
qui
sont l'un l'image dans un miroir de l'autre, comme la main droite et la main
gauche.
– a.
enantiomorphic
Encadrement d'un
nombre: deux valeurs l'une plus petite et l'autre plus grande que ce nombre.
Deux valeurs pour un nombre réel: une approximation par défaut et une
approximation par excès.
– ex. 3,1415 < p < 3,1416.
Ou alors, sans exclure les égalités: ![]() .
.
Le symbole pointe vers la valeur la plus petite (a < b, a est inférieur à b;
x > y; x est supérieur à y).
On note l'intervalle entre crochets: [3,141; 3,142
]; encadrement de π au millième près.
La longueur de l'intervalle est nommé: amplitude ou
ordre de grandeur de l'encadrement.
– v. Arrondi et
autres, réduites,
approximation, égal, inférieur, différent, supérieur, inégalité
– a. Approximation
by default (or by defect) and by excess
Endomorphisme: morphisme
d'un objet mathématique sur lui-même.
Un endomorphisme qui est aussi un isomorphisme est un automorphisme.
–
v. Types
de morphismes
– a. Endomorphism
Énième: en maths, (ou
nième ou ennième) s'écrit préférentiellement: n-ième. (Alain Rey).
– étym. de n, variable générique
désignant un nombre entier, avec le suffixe -ième, qui sert à former les
adjectifs ordinaux.
– a. nth, umpteenth. nth:
position n in a sequence for an arbitrary natural number n.

Ennéagone: polygone à 9
côtés.
Nonagone n'est pas correct car mélange
les racines linguistiques latines et grecques.
– v. Ennéagone
– a. nonagon or enneagon
Énoncé: exposition des
données de départ d'un problème.
– v. Hypothèse, proposition
– a. Statement of the problem
Ensemble:
regroupement
(collection) d'objets de même nature.
Le but est de le traiter globalement comme un tout, d'étudier ses propriétés en
tant qu'ensemble d'objets.
Un ensemble est défini soit en énumérant tous ses éléments.
– ex. {roi, dame, valet}
Ou en donnant une propriété caractéristique de chaque élément.
– ex. (les carrés parfaits).
– propriété majeure: ne comprend qu'un élément de chaque type; pas de doublons.
En outre, les éléments sont triés.
– ex. S = {1, 2, 10, 12, 23}
– symb. {…} les accolades
– type: Groupe, anneau, corps, classe.
– v. Ensemble, liste,
suite, série, vocabulaire
des structures algébriques
– a. Set
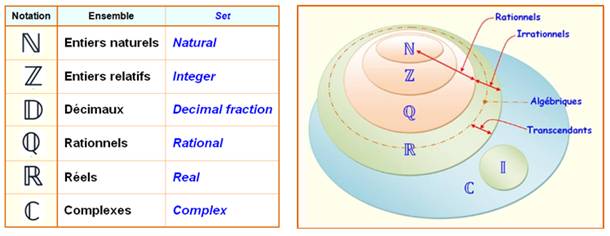
Ensemble des nombres: ensemble de tous les nombres de toute nature.
On distingue différents types de nombre et donc de sous-ensembles (Illustration).
– v. Ensembles de
nombres, classification
des nombres
– a. Number system: the numbers classified into sets
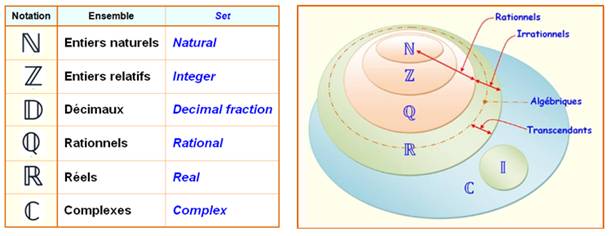
Ensemble de départ ou source
Ensemble d'arrivée ou but
Ensemble fini et ensemble produit: Voir
vocabulaire
des structures algébriques
Ensemble quotient: Voir Quotient (ensemble -)
Ensemble dénombrable ou infini dénombrable: qui comprend autant
d'éléments que n'en compte l'ensemble des entiers naturels.
Chaque élément peut être indexé par un entier sans omission, ni répétition.
Les deux ensembles sont équipotents.
Notez que l'ensemble est dénombrable mais pas fini (il y a une infinité de
nombres entiers naturels).
– note: On parle parfois de dénombrable pour une correspondance (bijection)
avec une partie seulement des entiers. Alors l'ensemble est dénombrable et
fini.
– ex. Les nombres pairs forment un ensemble dénombrable.
– v. Dénombrable et
continu, transfinis
– a. Countable set
Ensemble fermé, stable ou clos* pour une opération: une opération
entre éléments produit un résultat qui est dans cet ensemble. Dans le cas
contraire, on parle d'ensemble ouvert.
– ex. L'addition
des nombres entiers a pour résultat un nombre entier. Mais, ce
n'est pas le cas de la soustraction pour
laquelle le résultat peut être négatif. L'ensemble des nombres réels est stable par
soustraction, tandis que l'ensemble des entiers naturels ne l'est pas
– def. Ensemble dans lequel on a défini
une loi
de composition interne.
– a. Closed set and open set
Ensemble fermé et ouvert* ou partie fermée ou ouverte: en topologie,
un sous-espace topologique (Illustration).
Il est ouvert s'il ne contient aucun point de sa frontière. Il s'agit d'un
ouvert.
– a. Closed set and open set
Ensemble vide: ensemble qui ne
contient aucun élément.
– Noté
![]()
– a. Empty set: unique set having no elements
Ensemble de Mandelbrot: ensemble fractal
dit du "pou".
– v. Fractale de
Mandelbrot et Julia
– a. Mandelbrot set
Multiensemble*: il peut comporter plusieurs exemplaires d'un élément,
alors que l'ensemble n'a qu'un exemplaire unique.
– type: Groupe, anneau, corps, classe.
– v. Multiensemble,
– a. Multiset
Ensemble partiellement ordonné ou
poset: ensemble muni d'une relation d'ordre qui indique que pour certains couples d'éléments, l'un est plus petit
que l'autre. Tous les éléments ne sont pas forcément comparables, contrairement
au cas d'un ensemble muni d'un ordre total.
– a. Partially ordered set or poset for short: an arrangement such that, for
certain pairs of elements, one precedes the other.
Ensemble de définition
d'une fonction: en gros, c'est l'ensemble des nombres (entiers, réels …) où va
"atterrir" la valeur d'une fonction.
– ex. Si P = prix de n bouteilles d'eau à 2 euros, alors la fonction est: P(n)
= 2n et l'ensemble de définition est: ![]() , l'ensemble des nombres entiers.
, l'ensemble des nombres entiers.
– ex. Si l'aire d'un rectangle vaut: A(x) = (10 + L) (5+ l), l'ensemble de
définition est: ![]() , l'ensemble des
nombres réels au carré (carré, car deux dimensions en jeu).
, l'ensemble des
nombres réels au carré (carré, car deux dimensions en jeu).
Formellement: soit f une fonction à valeurs réelles (ou
autres), l'ensemble de définition de f est l'ensemble des réels x (ou autre
ensemble) pour lesquels l'image f(x) existe ou pour lesquels f(x) a un sens.
– a.
Domain of a function
Entier (nombre -): nombre rond, sans
décimale, positif et négatif.
– synonymes: entier relatif,
entier algébrique, entier rationnel.
– v. Nombres
Entier
naturel (nombre -): nombre entier positif.
Les nombres ordinaires pour compter.
– ensemble noté ![]() .
.
– synonymes: naturel, entier
naturel, entier positif.
– v. Nombres entiers naturels
– a. Natural numbers or whole numbers
Entier relatif (nombre -): nombre entier doté d'un
signe.
Ils sont positifs, négatifs ou nul.
– ensemble noté ![]() (le Z de Zahlen, nombre en allemand).
(le Z de Zahlen, nombre en allemand).
– v. Nombres relatifs
– a. Integer (du latin integer signifiant entier)
Entier de
Gauss: nombre complexe en
nombres entiers.
– a. Gauss integer
Série
entière: somme polynomiale ont les
termes comprennent un coefficient et une variable à des puissances successives.
– ex. 4 + x + 2x2 + …
– v. Somme de puissances
– Index
– a. Power series
Élément
entier (sur un anneau)**: généralisation des nombres algébriques
– a. Integral element
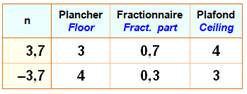 Entière (partie -): la partie entière de 12,34 est 12.
Entière (partie -): la partie entière de 12,34 est 12.
– notation: [12,34] = 12.
Les chiffres après la virgule (34)
forment la partie fractionnaire.
– a. Floor function,ceiling function, fractional
part
Entité mathématique: synonyme d'objet
mathématique.
Nom collectif pour désigner l'ensemble de tous des objets mathématiques:
figures géométriques, point, ligne,
surface, volume, nombres, matrices, vecteurs …
– a. Mathematical objects are either abstractions
from nature or abstract entities of which certain properties, called axioms,
are stipulated.
Entraîne: synonyme de
implique, à pour conséquence que …
– v. Implication
– a. Imply that
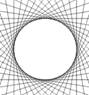
Enveloppe* l'enveloppe d'une
famille de droites est telle que chaque droite est tangente à la
courbe enveloppe.
De plus, chaque point de l'enveloppe doit admettre une droite de la famille
comme tangente à l'enveloppe.
– v. Enveloppe de la
cycloïde
– a. Envelope
Épicentre:
lieu
central où se produit ou d’où provient un phénomène.
En géophysique, l'hypocentre est le lieu à l'origine d'un séisme
et l'épicentre, sa projection à la surface
de la Terre.
– a. Epicenter and hypocenter
Épicyle: les planètes
tournent sur un épicycle qui lui-même tourne sur un (cercle)
déférent.
– v. Mouvement rétrograde
– a. Deferent and epicycle
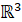 Épicycloïde: trajectoire d'un point d'un cercle qui roule
sans glisser sur un autre, le cercle directeur.
Épicycloïde: trajectoire d'un point d'un cercle qui roule
sans glisser sur un autre, le cercle directeur.
– types selon la quantité de points de rebroussement:
cardioïde (1, illustration),
néphroïde (2), ranunculoïde (5 comme cinq pétales)
– v. Surface
broutée par la chèvre
– a. Epicycloid
Équable (triangle -): triangle qui a le
même nombre pour périmètre et pour aire.
– équable veut dire constant
– v. Exemple
– a. Equable
 Équation: égalité algébrique
(polynôme = 0) de laquelle on cherche à calculer la valeur des inconnues, les
solutions ou les racines.
Équation: égalité algébrique
(polynôme = 0) de laquelle on cherche à calculer la valeur des inconnues, les
solutions ou les racines.
– ex. 2x – 10 = 0 =>
x = 5
– v. Résolution, solution
– v. Équation, Identité
– v. Equation
Définition:
une équation est une égalité
comprenant un ou plusieurs nombres inconnus désignés par des lettres. On
appelle ces nombres les inconnues de l'équation.
Une solution de l'équation est une valeur de
l'inconnue pour laquelle l'égalité est vraie.
Résoudre une
équation c’est trouver toutes ses solutions.
Principe
de résolution: une égalité reste
vraie si on additionne ou soustrait un même nombre aux deux membres de
l’égalité. Vraie également si on
multiplie ou on divise par un même nombre différent de zéro
les deux
membres de l’égalité.
Formellement: on appelle équation une relation de la
forme f(x) = 0, où f est une fonction d’une variable x réelle ou complexe. Il
se peut que l’équation ne se présente pas initialement sous la forme f(x) = 0,
mais il est toujours possible de l’y ramener.
Toute valeur x0,
pour laquelle la relation f(x) = 0 est vérifiée est appelée solution ou racine
de l’équation. Trouver toutes les racines, c’est résoudre
l’équation.
Si le problème
à résoudre comporte k variables, il faudra k équations distinctes pour trouver
les solutions.
Équation du premier degré ou
équation linéaire: ax + b = 0; solution x = -b/a
– v. Équation du premier degré
– a. Linear equation
Équation produit ou équation produit nul:
(ax + b) (cx + d) = 0; solutions x = –b/a et –d/c
– a. Zero-product
property: if ab=0, then a = 0 or b = 0
Équation du second degré ou équation
quadratique: ax² + bx + c = 0.
– v. Équation
du deuxième degré, discriminant
– a. Quadratic equation (du latin quadratus: carré)
Équation du troisième degré ou
équation cubique:
– v. Équation
du troisième degré
– a. Cubic equation
– après: Quartique, Quintique,
Sextique …
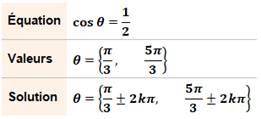
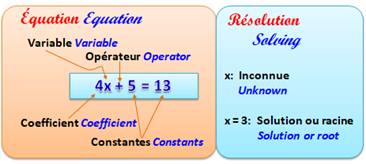
Équation trigonométrique: équation comportant
des lignes trigonométrique comme le sinus, le cosinus ou la tangente. Voir illustration
– v. Équation
trigonométrique
– a. Trigonometric
equation
Équation résolvante*: équation plus simple qui permet de résoudre
l'originale
– ex. Lagrange a montré que
pour résoudre une équation du
troisième degré, on peut se ramener à une équation résolvante de degré
2, en utilisant une expression polynomiale impliquant les racines
cubiques de l'unité
Équation diophantienne: équation avec
exclusivement des nombres entiers.
– v. Équation diophantienne.
– a. Diophantine
equation
Équation de Pythagore: équation
diophantienne permettant de trouver des triplets de Pythagore:
x² = y² + z²
– sol. x = k(m² + n²); y = k (m² – n²); z = 2kmn
avec k, m et n des nombres entiers.
– a. Pythagorean triple
Équation de la droite: équation de la
forme y = ax +b
– v. Affine, linéaire, premier degré
– v. Équation de la
droite, exemple en Fractions
unitaires, équation
du cercle
Équation algébrique ou équation polynomiale: l'équation du cercle, par exemple, est
une équation algébrique: x² + y² = 1.
Une équation telles que P(x) = 0 où P est un polynôme.
Elle définit un lieu géométrique qui est appelé une variété algébrique.
– a. Algebraic equation or polynomial equation
Équation aux dimensions* expression donnant
la correspondance d'une grandeur par rapport aux grandeurs fondamentales du
système d'unités
SI.
– ex. La vitesse s'exprime
par V= L/T ou mieux V = L .T-1
Plus complexe, la puissance
devient W = L2. M . T-3
– v. Équation aux dimensions
– a. Physical dimension, dimensional analysis
Équations
différentielles**, équations aux dérivées partielles**
Une
équation différentielle présente une relation entre une ou plusieurs fonctions
et leurs dérivées
Une équation
Ces équations sont l'outil fondamental de l'étude des systèmes
dynamiques: stabilité et évolution
de phénomènes périodiques, quasi-périodiques ou chaotiques.
– v. Différentiellle,
équations différentielles
– a. Differential
equation
Équations différentielles stochastiques (EDS)**
Une
équation différentielle qui prend en compte un terme aléatoire
(bruit blanc - Stochastique).
 – appli. Les EDS permettent de modéliser des
trajectoires aléatoires, tels des cours de bourse ou les mouvements de
particules soumises à des phénomènes de diffusion.
– appli. Les EDS permettent de modéliser des
trajectoires aléatoires, tels des cours de bourse ou les mouvements de
particules soumises à des phénomènes de diffusion.
– ex. (illustration): première EDS
proposée par Paul Langevin
dans le cadre de l'étude du mouvement
brownien.
– v. Marche de l'ivrogne, chemins sur réseaux
– a. stochastic differential equation (SDE) is a
differential equation in which one or more of the terms is a stochastic
process, resulting in a solution which is also a stochastic process.
Équerre: instrument en forme
de triangle rectangle
servant à tracer les angles
droits.
– étym. Vient du latin exquadrare, équarrir: donner une forme de parallélépipède à une
pierre, la rendre carrée, la dresser.
– v. Angle de 30°
– a. Set square écolier), Try square (artisans) >>>
– note:
en latin, Norma est une sorte d’équerre qui servait aux agrimensores (arpenteurs). II est devenu
ensuite un terme signifiant: règle, principe.
 Équiangle ou isogonal: figure dont les
angles sont égaux.
Équiangle ou isogonal: figure dont les
angles sont égaux.
Le triangle
équilatéral est équiangle.
Le carré est un quadrilatère équiangle.
– illustration: hexagone concave indirect equiangle
– v. Isoangle,
hexagone équiangle
– a. Equiangular, equiangular polygon
Équiangulaire: Voir spirale
équiangulaire >>>
Équidissection d'un
polygone: partage du polygone en k trianges d'aires égales.
– v. Dissection
– a. Equidissection: a partition
of a polygon into triangles of equal area.
Théorème de Monsky: un carré (ou plus
généralement un parallélogramme) ne peut être ainsi décomposé en un nombre
impair de triangles. La plupart des polygones n'admettent aucune
équidissection.
Équidistants: qui se trouvent à
la même distance.
– ex. Les points situés
sur la médiatrice
d'un segment sont
équidistant des extrémités du segment.
– ex. Les points situés sur la bissectrice
d'un angle sont
équidistant des côtés de l'angle.
– a. Equidistant
Équifacial ou
disphénoïde: polyèdre
dont toutes les faces sont les mêmes (congruentes).
Tous les polyèdres réguliers sont disphénoïdes.
Le tétraèdre régulier
est équifacial mais un tétraèdre équifacial peut avoir des arêtes de trois
longueurs différentes.
– a. Disphenoid
Équilatère (hyperbole
-): dont les deux asymptotes sont perpendiculaires.
Théorème de Brianchon-Poncelet: lorsqu'un triangle est inscrit dans une hyperbole
équilatère, son orthocentre est aussi sur l'hyperbole.
Théorème conique de Feuerbach: le lieu des centres des hyperboles équilatères
circonscrites à un triangle est le cercle d'Euler du triangle.
– a. rectangular hyperbola or equilateral hyperbola
Équilatéral (triangle
-): triangle
dont les trois côtés sont égaux.
– v. Triangle équilatéral
– a. An equilateral triangle has
three sides that are all the same length and three angles that all measure 60
degrees.
Polygone équilatéral: qui a tous ses côtés égaux. Il est régulier que si
ses angles sont égaux, s'il est équiangle.
– v. Plygone équilatéral
Équilibré: qui fait part
égale, qui est symétrique.
Numération ternaire équilibrée: qui utilise les chiffres: –1, 0, +1.
– v. Ternaire
Équipollents
(bipoints ou vecteurs): les vecteurs
sont égaux,
de même norme (longueur), parallèles et de même sens.
Les extrémités de deux d'entre eux forment un parallélogramme.
Les diagonales
ont même milieu.
– v. Vecteurs, vecteurs
libres, bipoint
– a. A vector is said to be an equal vector to another vector if they both
have the same magnitude and the same direction
Systèmes déductifs équipollents; en logique, dans
lesquels tout théorème de l'un est théorème ou axiome des autres.
Équipotents (ensembles
-): même quantité d'éléments.
Deux
ensembles en bijection sont équipotents.
Ils ont même puissance, ils sont "égaux".
– ex. L'ensemble des entiers et celui des nombres pairs
sont équipotents.
– étym. Du latin: aequus, égal et potens, puissant.
– v. Ensemble dénombrable
– a. Equinumerosity: two sets A and B are
equinumerous if there exists a one-to-one correspondence (or bijection) between
them.
Équiprobable: des événements qui
ont la même probabilité.
Si on suppose que tous les événements sont équiprobable, on dit que l'on fait
une hypothèse
d'équiprobabilité..
– étym. cas des six faces
du dé non truqué.
– a. Equiprobable
Équivalence
(démonstration par -, raisonnement par -): forme de déduction par enchaînement de propositions
équivalentes.
– v. Types de démonstrations
Équivalence (relation
d'-): les propositions
p et q sont équivalentes (p Û q)
si p implique q (p Þ q) et q
implique
p (q Þ p).
Énoncés qui expriment ce concept:
![]() P équivaut à Q;
P équivaut à Q;
![]() P est une condition nécessaire et suffisante pour Q
;
P est une condition nécessaire et suffisante pour Q
;
![]() Une condition nécessaire et suffisante pour P est Q
;
Une condition nécessaire et suffisante pour P est Q
;
![]() P si et seulement si Q
(parfois abrégé en P ssi Q, (anglais: iff) ;
P si et seulement si Q
(parfois abrégé en P ssi Q, (anglais: iff) ;
![]() Pour que P, il faut et il suffit que Q .
Pour que P, il faut et il suffit que Q .
– v. Propositions synonymesrelation d'équilvalence
– a. Equivalence
relation: a binary relation that is reflexive, symmetric and transitive.
Soit E un ensemble sur lequel existe une
relation d’équivalence R.
Si x est un élément de E en relation avec l’élément y de E, on dit que x est
équivalent à y.
Comme la relation R est une relation
symétrique, y est aussi équivalent à x ; on dit donc simplement que x et y sont
équivalents.
Ératosthène
(crible d'-): algorithme de recherche des nombres premiers.
– v. Crible
d'Ératosthène, Cribles
– a. Eratosthene sieve
Érgodique**: qui parcourt tous
les états possibles avec des probabilités égales.
La théorie ergodique appliquée à la théorie
du chaos.
– étym. Du grec: ergos, travail et hodos, le chemin.
– v. Théorie
ergodique
– a. Ergodic process
Exemple étudié par Poincaré: la probabilité pour
qu’après un battage assez long une carte occupe une place donnée
est indépendante de la position qu’elle occupait initialement. C’est parce
qu’ils admettent cette ergodicité que les joueurs font confiance au battage
(sans tricherie) des cartes pour rétablir une situation de "hasard"
avant de commencer une nouvelle partie.
Hypothèse ergodique: à l'équilibre, la valeur moyenne d'une grandeur calculée de manière statistique est égale à la moyenne d'un très grand nombre de mesures prises dans le temps. Formulation initialement par Ludwig Boltzmann en 1871.
Erlangen (programme
-)**: recherche qui vise à interpréter la géométrie par ses groupes de transformations.
Comment dégager une vision globale de toutes les
géométries existantes ?
Trouver les points communs: invariants,
actions de groupe.
– a. Erlangen program
Erreur: résultat faux dans une opération
– v. Preuve par neuf
– a. Error, cast out the nines, digital
root
Erreur de mesure: différence entre la valeur
donnée par la mesure et la valeur exacte (bien souvent inconnue) d'une
grandeur.
Pas nécessairement une erreur humaine.
Elle peur être aléatoire ou systématique.
Ne pas confondre avec incertitude sur la mesure.
– a. Observational error, measurement
error
Erreur absolue: écart (donc valeur absolue) entre valeur
mesurée et valeur théorique.
Erreur relative: valeur du rapport entre l'erreur absolue et la valeur
théorique. Elle peut être exprimée en pourcentage.
a. Absolute,
relative and percentage error
The
absolute error is the difference between the actual and measured value.
– notez: actual en anglais veut dire réel,
véritable (faux-amis)
En calcul numérique, on appelle erreur la
différence entre la valeur calculée d’un nombre et sa valeur exacte. Cette
erreur peut être positive ou négative selon que le calcul a été fait par excès
ou par défaut. La valeur exacte d’une erreur est, naturellement, inconnue et
souvent, même, son signe l’est aussi ; ce que l’on peut déterminer, c’est un
majorant de la valeur absolue de cette erreur : c’est ce qu’on appelle l’incertitude.
Par exemple, si on prend pour valeur de π = 3,14,
l’erreur commise est 3,14 - π. Une valeur approchée plus précise de π
étant 3,1416, l’incertitude peut être prise égale à 0,002 (qui est bien
supérieure à la valeur absolue de la différence 3,14 – 3,1416).
Escalier
(fonction en -): fonction constante par morceaux en nombre fini.
Famille des fonctions étagées (fonctions mesurables définies sur un espace
mesurable).
Une fonction réelle d’une variable réelle, définie sur un intervalle (a,
b), est une fonction en escalier si on peut partager (a, b) en intervalles
disjoints (a1, b1), (a2, b2), ... tels
que, sur chacun d’eux, la fonction soit constante.
– ex. Fonction constante, fonction signe (-1 avant
0 et +1 ensuite), fonction rectangulaire (une impulsion rectangulaire), etc.
La fonction valeur entière de x
comporte une infinité de segments. Certains la considère cependant comme
fonction excalier.
– intérêt: Elles sont utilisées pour résoudre des problèmes d'intégration.
– a. Step function or staircase function
Espace: l'espace usuel en
trois dimensions (3D).
Il est noté ![]() ("espace affine à trois
dimensions").
("espace affine à trois
dimensions").
Plus généralement, un ensemble sur lequel on a définit une structure
algébrique ou topologique.
On parle de géométrie dans l'espace.
– v. Plan
– a. Space, solid geometry or
stereometry or 3D geometry
Espace euclidien: espace de notre
géométrie habituelle, celle du lycée.
– v. Les Trois Géométries
– a. Eulidean space: the fundamental space of classical geometry.
Espace-temps: espace habituel à
trois dimensions, auquel on ajoute le temps comme dimension à part entière.
Notion essentielle de la relativité.
– ex. Un cube vu sous
différents angles change d'aspect; il en est de même pour un cube
spatio-temporel, à la différence que les quatre paramètres évoluent ensemble,
notamment les distances qui, paradoxalement, s'allongent ou rétrécissent.
– v. Espace-temps
– a. Spacetime
Espace vectoriel: un ensemble de vecteurs, que
l'on peut additionner entre eux, et que l'on peut multiplier par un scalaire.
– v. Vocabulaire
des structures algébriques
– a. Vector space or linear
space
Démarche dans le cadre de l'algèbre
linéaire: le vecteur a une représentation imagée dans l'espace : c'est
une flèche induisant une idée de force, de tendance orientée dans une certaine
direction et dont la longueur témoigne de son intensité .
En attachant un vecteur à chaque point de
l'espace, on crée un espace vectoriel. Imaginez
les forces qu'un aimant produit autour de lui.
Par un point donné O, on fait passer une
droite ; on donne un sens de parcours, une orientation et une longueur de
parcours ; c'est un vecteur d'origine O.
Les vecteurs dans leur ensemble sont munis de
deux lois qui confèrent à l'espace une structure particulière dite d'espace
vectoriel.
Ces deux lois sont; l'addition de deux
vecteurs (opération interne) et le produit d'un vecteur par un nombre réel
(opération externe).
L’espace vectoriel n'est pas seulement un
segment orienté ; ce peut être un espace de fonctions, de couples ou de
triplets, de nombres réels, etc.
Espace affine**: espace utilisé pour
la géométrie euclidienne (celle du lycée) sans les notions de distance et
d'angle. On s'intéresse au parallélisme et aux rapports de distance entre
segments parallèles.
On y utilise le théorème
de Thalès, mais pas celui de Pythagore.
C'est un espace vectoriel sans véritable origine. La translation y est reine.
– a. Affine space
Espace homogène**: espace sur lequel
un groupe agit de façon transitive.
Les éléments de l'espace forment une seule orbite selon l'action de groupe G.
Les espaces des géométries classiques sont des espaces homogènes pour
leur groupe de symétries.
– v. Action
de groupe, orbite
– a. Homogeneous space
Espace topologique**: structure d'ensembles en topologie.
Concept général permettant de définir la continuité, la convergence ou encore
la connexité.
Il est défini par un couple de deux ensembles E et T, un ensemble des parties
de E dont on précise les propriétés.
Un exemple simple mais ne présentant pas beaucoup d'intérêt est l'ensemble
topologique relatif aux nombres entiers (![]() )).
)).
– v. Groupe,
partition des ensembles, adhérence, dense, emboitements des espaces
– a. Topological space
Espace métrique**: cas particulier
d'un espace topologique où la notion de distance entre éléments est définie.
– ex. L'espace classique
3D euclidien.
– v. Géométrie euclidienne, emboitements des espaces
– a. Metric space
Espérance (d'une
variable aléatoire)* en probabilité, somme des produits des valeurs de la
variable par leur probabilité.
L’espérance (mathématique) est le moment d’ordre un.
– v. Moment
– a. The first moment is the
expected value
ET (conjonction): en logique,
opérateur qui donne un résultat vrai si et seulement si les entrées sont
vraies.
– v. Logique: ET
– a. AND
Si p et q sont deux propositions, la
proposition (p et q) est la proposition qui est vraie si et seulement si les
deux propositions p et q le sont toutes les deux vraies. Cette proposition est
aussi appelée conjonction des deux propositions p et q.
Étendue d'une série
statistique: différence entre la plus grande et la plus petite des valeurs
– v. Amplitude, série;
– v. Statistique
– a. Range
Étoile à cinq (six)
branches: figure inscrite dans un pentagone (hexagone)
régulier.
L'étoile à cinq branches est un décagone concave
régulier (ou équilatéral).
– v. Étoile à cinq
branches, étoile
mystique de Pascal
– a. Five-pointed star
Étoilé (polygone
régulier -): polygone régulier non convexe, présentant des branches régulières  d'étoile.
d'étoile.
– v. . Étoile à cinq
branches, étoile
à six branches
– a. Star polygon, stellation
diagram, The fifty-nine icosahedra
Étranger: deux nombre sont
étrangers, ou premiers entre eux, s'ils n'ont aucun diviseur commun
– v. Irréductible, PGCD
– v. Premiers entre eux (PEE)
– a. Coprime
Euclidien:
relatif
à Euclide. Mathématique
telle qu'Euclide l'a imaginée.
Division euclidienne: notre division classique avec dividende, diviseur,
quotient et reste.
Telle que a divisé par b se traduit par la relation a = q · b = r
–
v. Division euclidienne, modulo, PGCD
– a. Euclidean division or division with remainder
Espace euclidien: espace classique.
Espace affine (» homogène) avec une
définition de distance.
– a. Euclidean space
Géométrie euclidienne: notre géométrie
classique; elle suppose que les parallèles sont des droites qui ne se coupent
jamais (hypothèse faite par Euclide); on peut inventer d'autres géométries.
– v. Les trois géométries
– a. Euclidean geometry
Algorithme d'Euclide: méthode de calcul
du plus grand dénominateur
commun de deux entiers (PGCD).
– v. Algorithme d'Euclide
– a. Euclidean algorithm
Euler (1707-1783): Voir sa biographie et ses œuvres >>>
Euler a
laissé son nom à de nombreux objets ![]() mathématiques:
mathématiques:
Brique, caractéristique, cercle, chemin, constante, fonction gamma, fonction
Pi, formule, graphe, identité; indicatrice, invariant, points, totient, etc.
Célèbre formule
alliant cinq constantes majeures en
illustration.
Eurêka: Exclamation
attribuée à Archimède découvrant dans son bain la poussée des liquides sur les
corps immergés.
– v. Eurêka
Événement:
en
probabilité, lorsque la chose se réalise.
Partie réalisée de l'univers des probabilités.
Une probabilité lui est attribuée
Le dé tombe sur un multiple de 3 est un événement.
– v. Vocabulaire du dénombrement
– a. Event: a set of outcomes of an experiment
(a subset of the sample space) to which a probability is assigned.[
Événements certains,
possibles, contraires, incompatibles
– v. Probabilités
et statistiques, vocabulaire
du dénombrement
– a. Event
Exact: synonyme de juste.
Utilisé pour dire division exacte lorsque le reste est nul.
– v. Division
euclidienne
– a. Exact, exact calculation, correct calculaton, proper calculation, accurate
measure.
Exactitude: en métrologie,
aptitude à donner une mesure proche de la valeur réelle de la grandeur. On
parle alors d'erreur de mesure.
– v. Résolution, sensibilité, précision, fidélité
Excès (approximation
par-): 3,1416 est une valeur par excès de p = 3,14159
– v. Approximation, arrondi et autres
– a. Approximation by
default (or by defect) and by excess
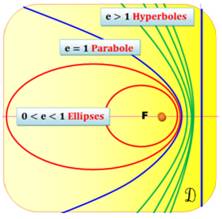
Excentricité d'une
conique: conique: lieu d'un point se déplaçant dans un plan tel le rapport de sa
distance à un point fixe F (le foyer) à la distance à une droite fixe (la
directrice) est une constante. Ce rapport est l'excentricité (e) de la conique.
– v. Excentricité
des conique
– a. eccentricity.
Exclu (principe du
tiers -): une proposition est vraie, ou bien sa négation est vraie; une troisième
possibilité n'est pas possible.
– v. Tiers exclu
– a. Law of excluded middle: for every proposition, either this proposition or
its negation is true.
Exeter (point -): point particulier
du triangle en rapport avec les médianes
– v. Droite d'Euler
– a. Exeter point
Exhaustion
(méthode d'-): Méthode permettant de calculer ou
de vérifier une grandeur au moyen d'approximations de plus en plus précise.
Technique
de calcul d'aires, de volumes et
de longueurs de figures géométriques complexes.
Archimède utilise cette méthode pour
calculer l'aire du segment de parabole
ou encore l'aire de la sphère.
La quadrature est la recherche de l'aire d'une surface (quadrature du cercle).
La rectification est la recherche de la longueur d'une courbe.
– a. Method of exhaustion
Exhaustive (recherche
-) : méthode dite aussi par force brute.
Recherche par examen systématique de toutes les possibilités.
Méthode adaptée aux recherches par ordinateurs.
– a. Exhautive method, brute-force procédure
Exinscrit (cercle – à
un triangle): cercle tangent
à un côté et au prolongement des deux autres; il y en a donc 3.
– v. Triangles et
cercles, cercles exinscrits
– a. Excircles of a triangle
Expérience
(aléatoire): action pouvant engendrer plusieurs résultats possibles.
Les types de résultats sont connus et chacun est possible, mais imprévisible.
– v. Probabilités
et statistiques
– a. Experiment (et pas experience !).
Explosion combinatoire:
cas
où un dénombrement des possibilités, comme dans les chemins possibles du voyageur de commerce, devient très grand,
trop grand pour être traité par un ordinateur. Le simple carré
latin subit ce phénomène: avec seulement sept cases on atteint soixante
mille milliards de possibilités de carrés différents.
– v. Légende de l'échiquier
–
a. Combinatorial explosion
Exponentielle
(fonction -)* fonction dont la puissance est la variable.
– fonction: y = ax
Si la base a vaut la constante e, l'exponentielle est dite
naturelle ou népérienne.
– v. Exponentielle
/ Logarithme
– a. Exponential function
Exponentiel: qui augmente
continument et rapidement.
En fait, augmentation comme une puissance (fonction exponentielle).
Exponentiation: mettre un nombre a
à la puissance n: an.
On obtient la énième puissance de a. a est la base et n l'exposant.
C'est une opération binaire non commutative.
– prop. an + m = an × am
– a. Exponentiation: an operation, written as bn, involving two
numbers, the base b and the exponent or power n, and pronounced as b raised to the power of n.
La fonction exponentielle est la fonction réciproque de la fonction logarithme
népérien.
Cette dernière (notée ln ou Log) est une application de l’intervalle ouvert ]0,
![]() [ dans
l’ensemble des nombres réels R, continue et strictement croissante.
[ dans
l’ensemble des nombres réels R, continue et strictement croissante.
La fonction logarithme admet une application réciproque qui est une application
de R  dans ]0,
dans ]0, ![]() [ ,
continue et strictement croissante. On l’appelle exponentielle et on la note
exp (x).
[ ,
continue et strictement croissante. On l’appelle exponentielle et on la note
exp (x).
Si à x correspond y par la fonction
Log (y = Log x),
à y correspond x par la fonction
exp (x = exp y) :
y = Log x ⟺ x = exp y.
La courbe représentative de la fonction
exponentielle (dans un repère orthonormé) est symétrique de celle de la fonction
Log par rapport à la première bissectrice.
Quel que soit le nombre entier relatif n, on démontre que exp (n) est égal à en
(e étant le seul nombre pour lequel le logarithme népérien vaut 1 : e =
2,71828...).
a
= exp(1) = e et ln(a) = ln(e) = 1.
On convient d’écrire, pour tout nombre réel x, exp(x) = ex.
On dit que la fonction exponentielle est la fonction exponentielle de base e.
Exposant: dans ab, b est l'exposant.
Cela veut
dire que a est élevé à la puissance b.
– ex. 23 = 2 x 2 x 2 = 8. On
lit: 2 puissance 3 et pas 2 exposant 3.
– v. Calculs pratiques, exponentiel, puissance, base
– a. Powers are also called exponents or indices.
– ex.
8² could be called 8 to the power
2 or 8 to the second power, or
simply 8 squared.
Expression:
suite
de termes comportant des lettres et des nombres: des constantes, des variables,
des opérations, des fonctions, des parenthèses.
Une expression est exprimée selon des règles établis, une syntaxe logique.
Une formule exprime une relation entre expressions. Ex. 3x + 2 > 5y – 3, le
tout est une formule formée de deux expressions.
Un monôme désigne une expression algébrique ne
comportant qu'un seul terme; un binôme en compte deux;
un trinôme, trois; etc.
L'expression peut être simple: 4 + 8; linéaire: 4x +
8; quadratique: 4x² + 8x – 4; rationnelle:
(x +1) / (x – 2); ou plus complexe: ![]() .
.
– v. Bases de l'algèbre,
littéral, polynôme, calcul, priorité des
opérations, chaine d'opérations
– a. Algebraic expression
Expression numérique: ne comporte que des
nombres.
– ex. 2(10 – 3) et 1/10 +
2/100 sont des exemples d'expressions numériques pour respectivement 14 et
0,12.
– a. Numerical expression: A numerical expression in mathematics can be a
combination of numbers, integers combined using mathematical operators such as
addition, subtraction, multiplication, or division.
Expression littérale ou algébrique: comporte aussi des
lettres.
Ces lettres représentent des nombres qui ne sont pas fixés, des variables.
Se prête aux calculs algébriques.
– v. Bases de
l'algèbre
– a. Literal expression
Extension:
un
ensemble E est défini en extension s’il est défini par la liste de tous ses
éléments, par énumération de ses éléments.
– ex. l’ensemble des voyelles de l’alphabet français est défini en extension
lorsqu’on donne la liste des six voyelles a, e, i, o, u, y ; cet ensemble est
noté : { a, e, i, o, u, y } en faisant figurer entre accolades la liste de ses
éléments (séparés par une virgule, et chacun d’eux n’apparaissant qu’une fois).
– contraire: définition par compréhension en
énonçant les propriétés des éléments. Ex.ensemble des
nombres pairs.
– a. definition of a set by its list of elements, the roster method or
enumeration notation
Extérieur: qui est en dehors.
– ex. une droite extérieure à
un cercle n'a
pas de point commun avec ce cercle.
– v. Intérieur
 – a. Outside
– a. Outside
Extérieur (angle -) ou angle
externe: angle formé
par un côté du polygone
et le prolongement du côté.
L'angle externe est supplémentaire de l'angle interne, et non explémentaire.
– a. types d'angles
– a. Exterior Angle: angle formed by two adjacent sides outside the polygon.
Externe (loi de
composition -)*: une application sur l'ensemble E est une application F ×
E dans E ou E × F dans E, les ensembles E et F étant différents (si
identique: loi de composition interne).
– ex. an = b avec a
et b réels et n entier est une application: ![]()
– v. Loi de composition, loi de composition interne
– a. Binary relation, law of composition
The law of composition is a function or application that takes two elements
from two given sets and assigns them to another element, belonging to one of
the two sets.
Extraire une racine
(extraction): calculer la racine d'un nombre.
– ex. Extraire la racine carrée de 121; je trouve 11, car 11 × 11 = 121.
– a. Compute square root, finding a root, method to work out square roots
Extrapolation:
prolonger
au-delà des valeurs connues.
Estimation de valeurs en dehors des valeurs observées d'une fonction connue empiriquement.
– v. Prédiction, interpolationr
– a. Extrapolation, a type of estimation
Extrémité: chacun des points limitant un segment.
– v. Sommet, origine
Extremum: nom générique pour minimum ou maximum.
–
pl. des extremums, des minimums, des
maximums.
– a. Extremum
Mot employé pour indiquer qu’une fonction f
d’une variable réelle x admet un maximum ou un minimum, sans préciser s’il
s’agit de l’un ou de l’autre.
S’il y a extremum pour une valeur x0 de la variable, alors la
dérivée de la fonction s’annule pour cette valeur x0.
La réciproque n’est vraie que si la dérivée s’annule en changeant de signe.
![]()
|
Voir |
|
|
Aussi |
|
|
Autres |
|
|
Cette page |


