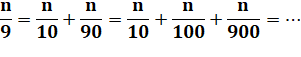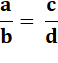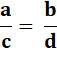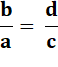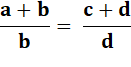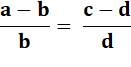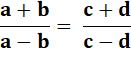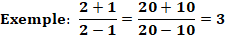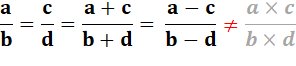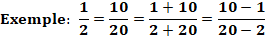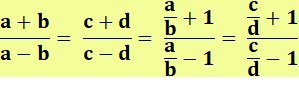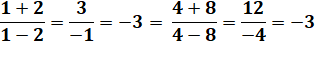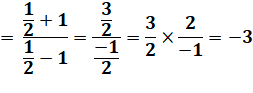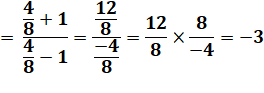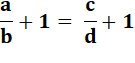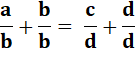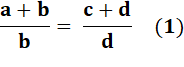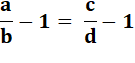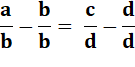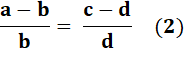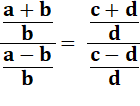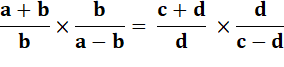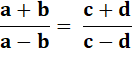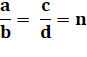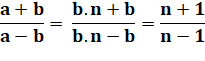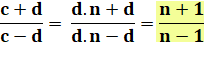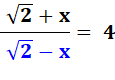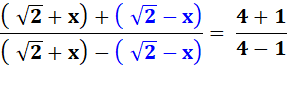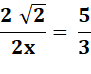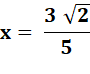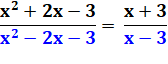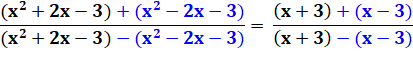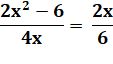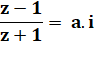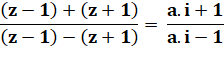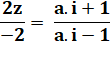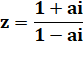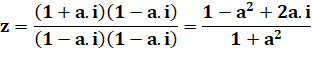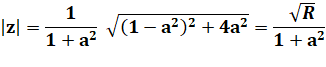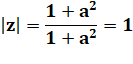|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
FRACTIONS Identités Identités remarquables avec les
fractions. Le
componendo et dividendo des anglo-saxons. Pratique
pour simplifier des fractions "compliquées". Componendo = composition en
latin et en italien. Dividendo =
dividende |
Le saviez-vous
|
Cette
identité est utilisée pour expliquer que le développement décimal des
fractions est périodique:
|
Voir Propriété des divisions par 9, 99, 999…
|
|
||
|
Noms en latin |
Propriété |
|
|
Identité de départ |
avec Cette égalité entraîne
toutes les égalités suivantes et réciproquement. |
|
|
Alterando |
|
|
|
Invertendo |
|
|
|
Componendo |
|
|
|
Dividendo |
|
|
|
Componendo et
dividendo |
|
|
|
Autre |
|
|
Démonstration express de ces dernières relations
|
|
|
|
|||
|
Formule
avec
|
|
|
|
|
Exemple
|
|
Attention: la valeur des fractions données n'est pas
égale à celle des nouvelles fractions. |
|
|
|
||
|
Componendo Ajoutons 1 de chaque côté de l'égalité. Remplaçons 1 par une fraction égale à 1. Légitime car b n'est pas nul. Addition des fractions de même dénominateur |
|
|
|
Dividendo Retirons 1 de chaque côté de l'égalité. Remplaçons 1 par une fraction égale à 1 Addition des fractions de même dénominateur |
|
|
|
Componendo et
dividendo Divisons (1) par (2). Légitime car a-b n'est pas nul. Divisions changée en produit en prenant la fraction inversée. En effectuant le produit et en simplifiant |
|
|
|
|
||
|
Notons n la valeur de la fraction. Alors. Remplaçons dans l'identité finale. Les deux fractions sont bien égales et, nous avons sa valeur en
fonction du rapport n initial. |
a = b.n
et c = d.n
|
|
|
|
||
|
L'identité finale entraîne l'identité initiale. Produit en croix. Simplification. Produit en crois à l'envers. |
(a + b)(c – d) = (a – b)(c + d) ac–ad+bc–bd
= ac+ad–bc–bd 2bc = 2ad bc = ad
|
|
|
|
||
|
Résoudre cette équation. Application de componendo et divendo (C&D). Calcul. Produit en croix. Finalement |
|
|
|
|
||
|
Résoudre cette équation. Application de C&D Calcul Produit en croix. Solution. Retenue. |
12x² – 36 = 8x² 4x² = 36 x²
= 9 x = 3 ou – 3 x =– 3 Car x = 3 induit
un dénominateur nul dans l'identité de départ. |
|
|
|
||
|
Fraction avec deux nombres complexes et qui est purement imaginaire. |
|
|
|
Quelle est la valeur du module du nombre complexe z ? |
||
|
Application de componendo et divendo (C&D). Calcul. Inversion du signe. Multiplication par le conjugué pour avoir un
dénominateur purement réel. Calcul du module; Avec z = a+ib => Calcul de R. Conclusion. |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()