|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Bases de numération Principe / Méthode de conversion Pourquoi nous
comptons avec 10 chiffres? Pourquoi les ordinateurs ne comptent qu'avec deux chiffres?
Pourquoi, il y a des exceptions comme pour compter les heures ou les angles?
Etc. |
|
En base B, on a:
|
Quelle est la valeur
de 5 x 6 x 7 ? |
|
– Index par rubriques principales |
|
|
|
|
||
|
Chiffres
& Nombres |
|
|
|
Décimal |
|
|
|
|
||
|
Comparaison |
|
|
![]()
|
Autres
bases |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Conversion |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Tables |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
![]()
|
|
|||
|
Base 2
et base 3 Quels
sont les nombres qui s'expriment avec de 0 et des 1 seulement depuis la base
2 jusqu'à la base k = 3 ? Historique Nombres mis en évidence par Daniel Mondot en 2008
et enregistrés sous OEIS A146025 |
Exemple
pour les nombres de 10 à 50 en base 2 et en base 3 10, [1, 0, 1, 0], [1, 0, 1] 12, [1, 1, 0, 0], [1, 1, 0] 13, [1, 1, 0, 1], [1, 1, 1] 27, [1, 1, 0, 1, 1], [1, 0, 0, 0] 28, [1, 1, 1, 0, 0], [1, 0, 0, 1] 30, [1, 1, 1, 1, 0], [1, 0, 1, 0] 31, [1, 1, 1, 1, 1], [1, 0, 1, 1] 36, [1, 0, 0, 1, 0, 0], [1, 1, 0, 0] 37, [1, 0, 0, 1, 0, 1], [1, 1, 0, 1] 39, [1, 0, 0, 1, 1, 1], [1, 1, 1, 0] 40, [1, 0, 1, 0, 0, 0], [1, 1, 1, 1] |
||
|
Avec la
base 4 |
Exemple
pour les nombres de 10 à 500 en base 2, en base 3 et en base 4 81, [1, 0, 1, 0, 0, 0, 1], [1, 0, 0, 0, 0], [1, 1, 0, 1] 84, [1, 0, 1, 0, 1, 0, 0], [1, 0, 0, 1, 0], [1, 1, 1, 0] 85, [1, 0, 1, 0, 1, 0, 1], [1, 0, 0, 1, 1], [1, 1, 1, 1] 256, [1, 0, 0, 0, 0, 0, 0, 0, 0], [1, 0, 0, 1, 1, 1], [1, 0, 0, 0, 0] 273, [1, 0, 0, 0, 1, 0, 0, 0, 1], [1, 0, 1, 0, 1, 0], [1, 0, 1, 0, 1] 324, [1, 0, 1, 0, 0, 0, 1, 0, 0], [1, 1, 0, 0, 0, 0], [1, 1, 0, 1, 0] 325, [1, 0, 1, 0, 0, 0, 1, 0, 1], [1, 1, 0, 0, 0, 1], [1, 1, 0, 1, 1] 336, [1, 0, 1, 0, 1, 0, 0, 0, 0], [1, 1, 0, 1, 1, 0], [1, 1, 1, 0, 0] 337, [1, 0, 1, 0, 1, 0, 0, 0, 1], [1, 1, 0, 1, 1, 1], [1, 1, 1, 0, 1] |
||
|
Avec la
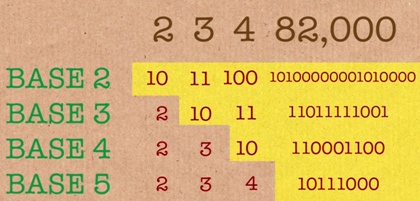
base 5 Un seul
nombre avec 0 et 1 pour les bases 2, 3, 4 et 5. Sans doute pas de nombre supérieur, mais non
prouvé. |
82 000, [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0], [1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1], [1, 1, 0, 0, 0, 1, 1, 0, 0], [1, 0, 1, 1, 1, 0, 0, 0] |
||
Présentation de cette propriété par Numberphile
|
|
Why 82,000 is an
extraordinary number – Numberphile
|
En base B, on a:
Quelle est la valeur
de: |
30 => 3B + 0 = 4 x
6 = 24 B = 8 34 => 3x8 + 4 = 28
=> B confirmé 5 x 6 x 7 = 210 = 3 x
64 + 2 x 8 + 2 = 322 en base B = 8. |
![]()
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()
Renvois de liens
>>> Quatre-vingt en français
>>> Base
hexadécimale
>>>
Système décimal
>>> Bases de numération
>>>
Exemple
avec 1000
>>> Bases particulières
>>> Bases mixtes
>>> Construction des
nombres
>>> Noms particuliers
>>> Principes de
numération
>>> Bases cosmiques
>>> Contexte historique
>>> Les mains
>>> Valeurs
positionnelles