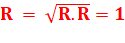![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page For
this page, refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
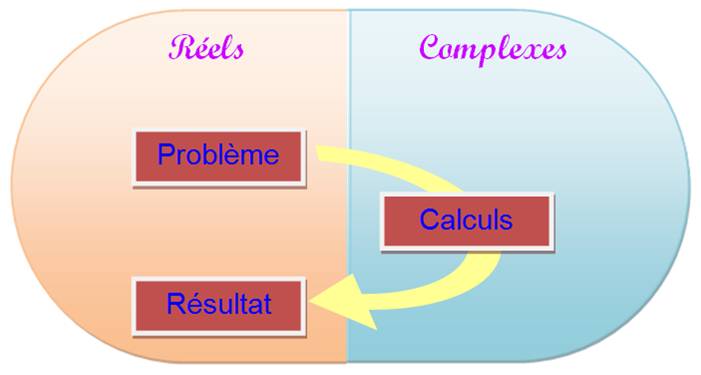
NOMBRES COMPLEXES Est-ce que l'imaginaire est
complexe? Pour vous faire une idée,
allez voir sur cette page:
|
|
Je
vous ai mis zéro; mais pourquoi m'avoir rendu une page blanche? – Mais,
M'sieur ce sont des nombres imaginaires ... |
|
Allons
! Résolvons ces problèmes sans complexes. |
Voir Pensées & humour
|
|
|||
|
Définition
où a et b sont des nombres
réels, et i un "nombre imaginaire" tel
que: i² = – 1 soit: i = Voir Notation symbolique de i = racine de –1 – Sa légitimité ?
Intérêt
|
|||
|
|
|
|
|
|
Voir Inversion géométrique et son effet
de levier / Multiplication rapide
/ Brève 62-1230
(Trigo-exponentielles)
|
|
||
|
Rappel fondamental Le nombre i est le nombre complexe dont le carré est
égal à –1: Il est racine du polynôme x² + 1 = 0. On le note symboliquement: Illustration
graphique
Ici, cette relation est évidente puisque a, b et c ont
pour longueur le rayon du cercle:
Intuitivement
|
||
|
|
|
|
Le
plan complexe (d'Argand ou de Gauss)
L'angle
|
|
Voir Nombres de
Gauss: entiers sur le plan complexe / Abscisse angulaire
/ Argand / Gauss

Voir Forme des complexes:
cartésienne, polaire et exponentielle
|
|
|
|
Actuelle
(due à Hamilton)
Polynômiale
(attribuée à Cauchy: 1789-1857)
|
|
|
Trouvaille
du "nombre" i qui permet la création du nouveau monde des nombres
complexes aux applications multiples. Vous
allez découvrir comme effectuer les quatre opérations classiques, effectuer des calculs en utilisant de identités remarquables, etc. Remarquez que: i = Vous n'imaginez pas la puissance
de l'imaginaire … |
Voir Portail
des nombres complexes
|
|
|
|
|
|
![]()
|
Suite |
|
|
Terminale |
|
|
Voir |
|
|
Cette page |
![]()
|
Je
recommande ce site |
Les dimensions expliquées en relief
animé de Jos Leys, Étienne Ghys et Aurélien Alvarez – Le téléchargement
mérite un peu de patience. Les animations et les explications valent vraiment
le détour … En passant par les
fractales et les nombres complexes |