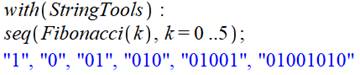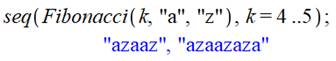|
||||||||||||||||||||||||||||||||
![]()
|
MOT BINAIRE FIBONACCI Construction d'une suite
binaire à la manière de celle des nombres de Fibonacci: récurrence sur les
deux dernières valeurs. Le mot Fibonacci est de longueur
infinie. Il possède des instances de rang k. Le mot Fibonacci est étudié sur cette page dans sa version binaire (0, 1). Ces chiffres
peuvent être remplacés par des lettres ou des symboles. |
Anglais Fibonacci word
The infinite
Fibonacci word is a specific infinite sequence in a two-letter alphabet.
|
|
||
|
Comme
pour la suite de Fibonacci,
on commence à poser deux valeurs de départ.
|
M1 = 1 et = 0 |
|
|
Puis on
fixe une règle de construction par récurrence: concaténation (juxtaposition)
des deux derniers mots. |
M3 = M2M1
= 01 M4 = M3M2 = 010 M5 = M4M3 = 01001 |
|
|
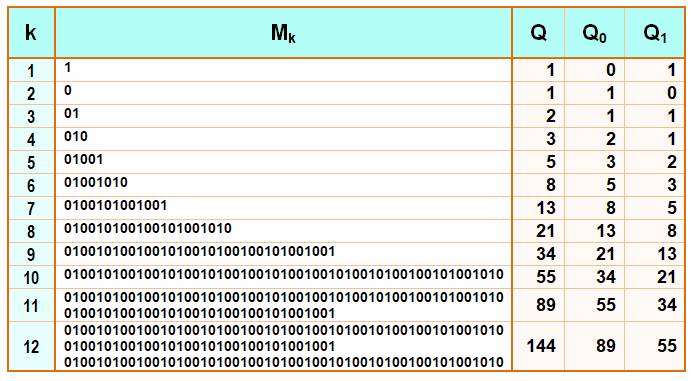
Les douze premiers mots Fibonacci Les trois colonnes de droite indiquent la quantité
de chiffres, la quantité de 0 et celle de 1. On y retrouve les nombres
de Fibonacci, eux-mêmes.
Le mot Fibonacci commençant avec 0, 1, 10 … est
complémentaire de celle-ci; La suite de nombres est nommée suite binaire
dorée ou la suite du lapin ce qui constitue un jeu de mot en anglais:
rab-bit sequence. |
||
|
|
|||
|
Morphisme (substitution rule) |
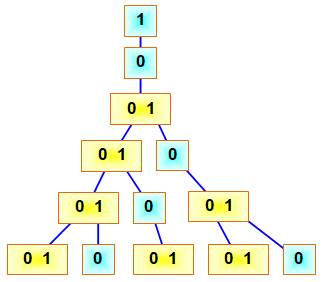
Le mot de Fibonacci peut
aussi être construit par un procédé de substitution. Pour passer d'un mot au
suivant, les 1 deviennent 0 et les 0 sont remplacés par 01. Il s'agit d'un morphisme
(une substitution) tel que:
|
|
|
|
Premiers chiffres |
De part
leur construction, les premiers
chiffres sont identiques jusqu'au rang égal au nombre de Fibonacci Fk-1. Conséquence: en poursuivant,
ce début du mot se stabilise sur un nombre de plus en plus grand de chiffres.
Le mot infini qui apparaît est le mot infini de
Fibonacci. Le nombre réel dont
l'écriture binaire est le mot Fibonacci infini est, comme les nombres Pi et
e, un nombre transcendant (racine
d'aucune équation polynomiale à coefficients entiers). Voir Suite
binaire dorée avec graphe |
||
|
Derniers chiffres |
Les derniers chiffres
oscillent entre deux valeurs. Par exemple pour les deux derniers, on trouve
successivement: 01 et 10. Les précédents sont
identiques. Voir programmation |
||
|
Palindromes |
En supprimant les deux
derniers chiffres le nombre est palindrome. |
||
|
Exclusion |
Jamais de configurations
en 000 ou 11. |
||
|
Chiffre n |
Phi est le nombre d'or. Les crochets
vers le bas indiquent que l'on ne retient que la partie entière. |
||
|
|
||
|
Mot de Fibonacci avec procédure
récursive
|
Commentaires La procédure MF calcule le mot Fibonacci de rang m
+ 2; les deux premiers étant inclus dans la procédure [0] et [0,1]. Justement si m = 0 ou m = 1, on forme les mots
Fibonacci [0] et [0,1]. Si m est différent, on demande le calcul de MF
pour les deux précédents. Le programme développe un procédé récursif
en faisant appel à lui-même. L'appel à la procédure tient compte du décalage
(k-2). Le résultat f est mis en forme en concaténant la liste (cat). Résultat imprimé (print) en bleu. |
|
|
Mot de Fibonacci avec instruction
dédiée
|
Le logiciel Maple dispose d'une instruction dédié
au mot Fibonacci. Il est évidemment possible d'introduire d'autres valeurs
initiales. Notez que ce logiciel numérote à partir de 0. Résultat en bleu: les six premiers mots Fibonacci. Puis un mot Fibonacci avec l'alphabet (a, z). Voir Anaanana |
|
|
Identification des derniers
chiffres
|
Réinitialisation et appel au logiciel de
manipulation des chaines de caractères (string). Lancement d'une boucle d'examen des mots
successifs de Fibonacci. Mot de Fibonacci dans "a" et sa
quantité de chiffres dans "qa". Formation de la suite des quatre derniers
chiffres avec (seq de 0 à 3) que l'on concatène (cat) et que l'on inverse
avec Reverse. Conversion en décimal pour mieux apprécier
l'alternance. Résultat en bleu, à gauche. En isolant les huit derniers chiffres:
|
|
Voir Programmation – Index
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Numerati/BINAIRE/FibonMot.htm
|
![]()