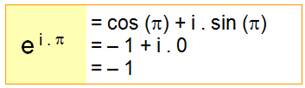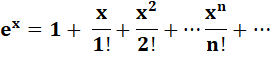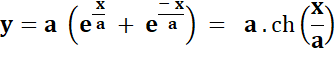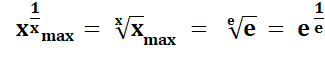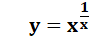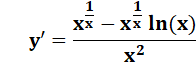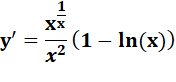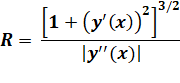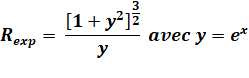NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Analyse
Débutants Exponentielle	EXPONENTIELLE				Glossaire Général
INDEX Arithmétique Algèbre Analyse	Introduction	Valeur	Fractions	Analogies
		Propriétés	Formules	Dénombrements
		Base	Dévelop e^x
		Sommaire de cette page >>> Irrationnel & transcendant >>> Propriétés de "e" et "i" >>> Fonction exponentielle >>> Exponentielle & puissance >>> Chaînette >>> Maximum – Curiosité >>> Courbure maximale de l'exponentielle

Propriétés de la CONSTANTE "e"

On se retrouve enchaîné (en chaînette!) à la trigonométrie.

C'est un peu complexe, ou alors, imaginaire.

On part à la dérive …

IRRATIONNEL & TRANSCENDANT
e	Irrationnel Transcendant	Démonstration par Lambert en 1761 Démonstration par Hermite en 1873
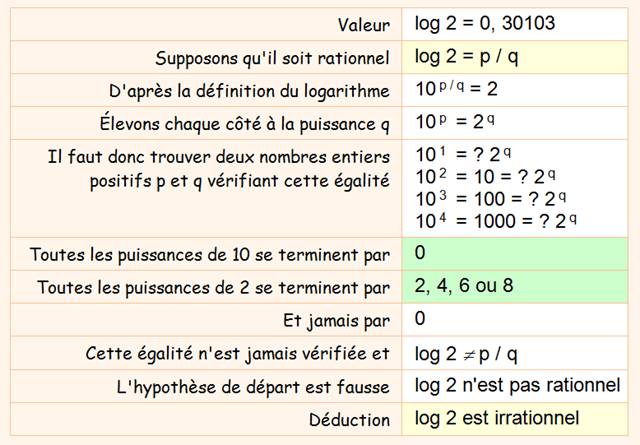
Approche avec log 2

Approche avec log 3

Approche avec la formule en factorielles

Voir Fraction

QUATRE CONSTANTES LIÉES
Euler et ses formules La formule " magique " des quatre constantes arithmétiques a été mise au point par Euler , sur des indications d'Abraham de Moivre. Formule élégante, difficile à interpréter, mais prouvée! Se calcule à partir de la formule générale en thêta, trouvée par Euler. L'application de cette formule montre la relation à quatre constantes.

Voir Déclinaison de ces formules / Puissance de l'imaginaire / Formule avec le nombre d'or

PROPRIÉTÉS de la fonction EXPONENTIELLE
Dérivée Formulation Développement Limite Complexe	Le taux de variation de e^x au point x = t vaut e^t. La fonction exponentielle est égale à sa dérivée. Seule fonction ayant cette propriété. Solution de l'équation différentielle la plus simple. La fonction exponentielle est égale à la somme infinie des inverses des factorielles des nombres successifs. Newton 1665 Voir Somme suites infinies Avec z = x + iy

Autres Propriétés / Suite en Formules produisant e / Dérivée / Complexes

Voir Brève 769

EXPONENTIELLE & PUISSANCE

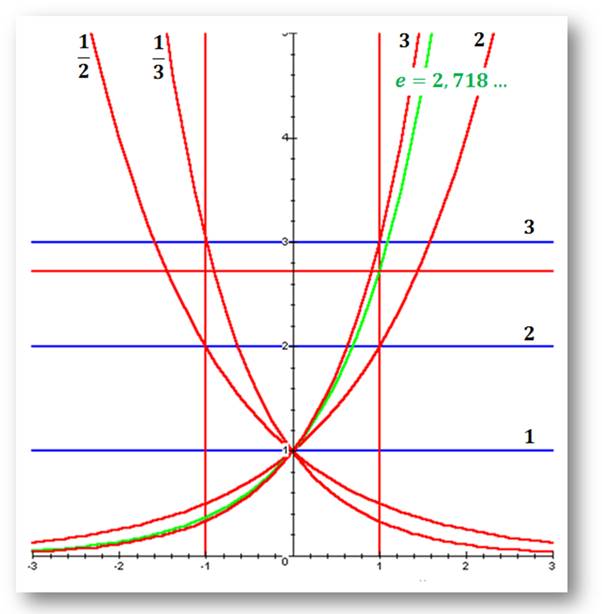
Courbes a ^x selon la valeur de a Toutes les courbes passent par x = 0 et y = 1. Dans un sens pour x > 1, symétriques pour x < 1. Elles coupent la droite x = 1 (ou -1) en des valeurs de y particulières (droites bleues) À noter La courbe avec a = 2 donne la croissance des puissances de 2. Ces courbes montrent l'allure des progressions géométriques La courbe exponentielle est une courbe puissance particulière (verte).

CHAÎNETTE
Courbe de la chaînette Forme d'une chaîne pendante tenue par deux points. Avec ch : cosinus hyperbolique Illustration selon la valeur de a On repère facilement chaque courbe, car elle passe par x = 0 et y = a.

Voir Igloo / Cycloïde

MAXIMUM – Racine énième de n
Problème de Steiner Ce problème a été formulé et résolu par Jakob Steiner en 1850. Quelle est la valeur qui maximalise la valeur de la racine énième de x?		Steiner's calculus problem The problem of finding the maximum of f(x) = x^(1/x) was posed and solved by the Swiss mathematician Jakob Steiner (1796-1863) in 1850. Voir Références
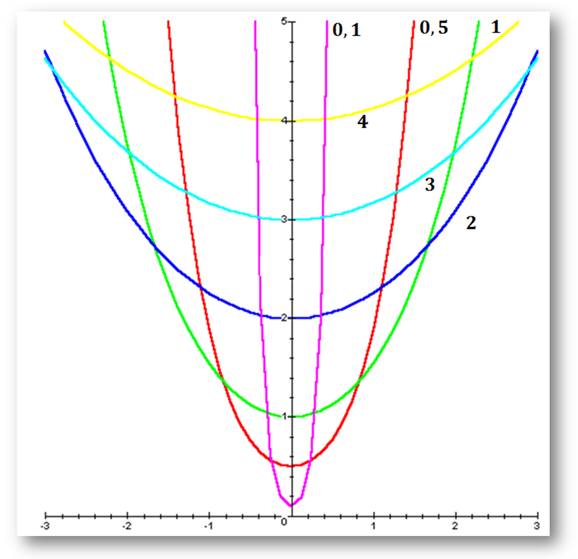
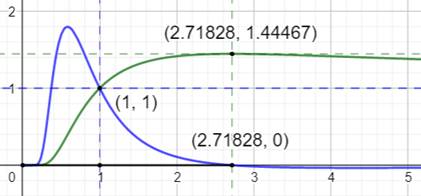
Courbe verte: la fonction Courbe bleue: sa dérivée Nulle pour ln(x) = 1 soit x = e	La courbe passe naturellement par le point {1, 1}. Elle tend asymptotiquement vers 1 pour x tendant vers l'infini.
La fonction x^x^x^x... (x puissance x, puissance x, etc. jusqu'à l'infini) a une limite si x est compris entre (Euler): e ^-e = 0,065 988 et e ^1/e = 1,444 667. Voir Nombre 1, 4446678 … / Valeurs de e puissance e
Calcul avec Maple evalf[50](exp(exp(-1))); 1.4446678610097661336583391085964302230585954532423 Note: exp(-1) = e^-1 = 1/e
Extrait du texte de Steiner Über das größte Product der Theile oder Summanden jeder Zahl- Steiner – pdf
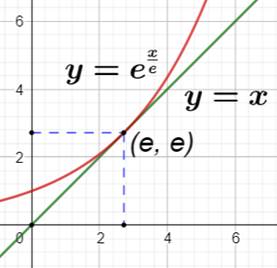
Démonstration sans la dérivée Sur le graphe présenté: En élevant à la puissance 1/x

Voir Brève 815

Courbure maximale de l'exponentielle		haut
Rayon de courbure de l'exponentielle Quelles sont les coordonnées du point de l'exponentielle y = e^x ayant le rayon de courbure minimum (le coude de l'exponentielle) ? Notez que le rayon de courbure est l'inverse de la courbure. Nous cherchons donc le point de courbure maximum. Son calcul Le rayon de courbure est défini par une fraction avec la dérivée seconde au numérateur et la dérivée première au dénominateur. Dans le cas de l'exponentielle ces diverses dérivées sont égales: y = y' = y" = e^x	Formule du rayon de courbure Cas de l'exponentielle
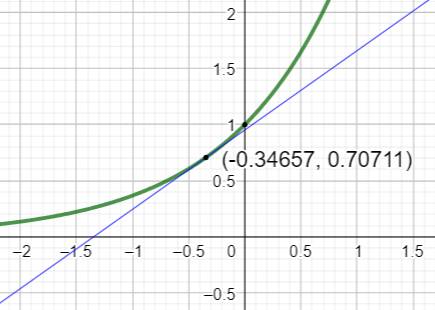
Calcul Pour information Le rayon de courbure au point (x = 0; y = 1) est égal à 2√2 = 2,828427… Graphe de la fonction exponentielle et point de rayon de courbure minimum

Suite	Valeur de la constante "e" Base des logarithmes Développement de e^x
Voir	Cercle Constantes Courbes élémentaires Courbe de charge d'un condensateur Exposants et puissances Exposants et puissances – Index Logarithmes Nombre d'or Pi Théorie des nombres
Sites	Steiner's Calculus problem – Wikipedia Steiner's Problem – Wolfram MathWorld OEIS A073229 – Decimal expansion of e^(1/e). Algebraic and transcendental solutions of some exponential equations** – Jonathan Sondowa, Diego Marques – 2009 Steiner's calculus problem Über das größte Product der Theile oder Summanden jeder Zahl- Steiner - pdf
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/ExpoProp.htm