NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 11/03/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométrie
Débutants Géométrie	Courbes étonnantes				Glossaire Géométrie
INDEX Courbes Géométrie	Cercle	Ellipse	Cycloïde	Lemniscate
		Sommaire de cette page >>> Approche >>> Cycloïde – Définition >>> Propriétés >>> Historique

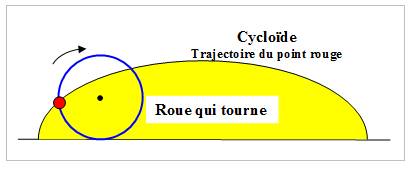
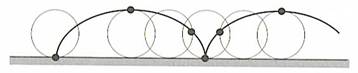
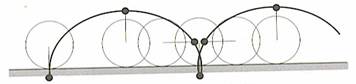
CYCLOÏDE

Ou Roue d'Aristote, Roulette de Pascal

Lorsque tu es chez elle,

d'où que tu partes

tu arrives toujours à l'heure !

La roulette est une ligne si commune,

qu'après la droite et la circulaire,

il n'y en n'a point de si fréquente.

Pascal 1623 – 1662

APPROCHE
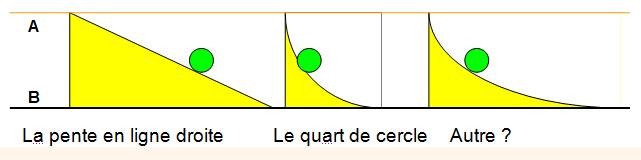
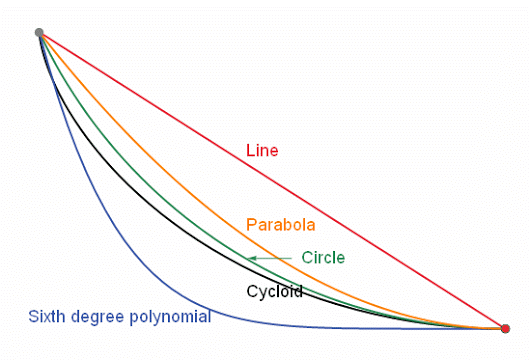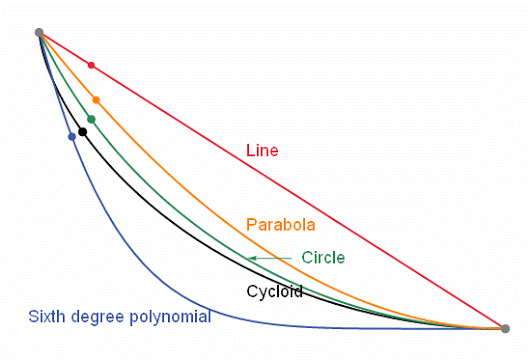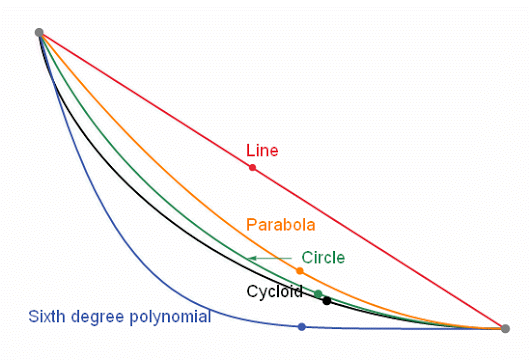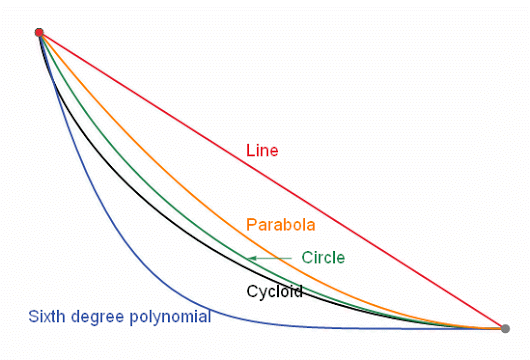
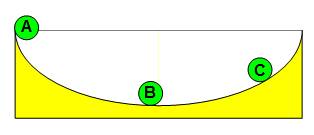
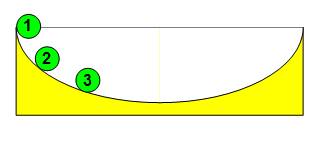
Question Je veux descendre une pente le plus vite possible Quelle est la piste la plus rapide ? La régularité de la droite ou une courbe qui impose une vitesse plus rapide au départ? Réponse C'est la CYCLOÏDE C'est la courbe de descente la plus rapide pour aller de A à B, ou de A à C, etc. Avec en prime, le fait que Quel que soit le point de départ ( 1, 2, 3 …), on arrive en bas en même temps.

CYCLOÏDE –Définition

Géométrique

C'est le parcours de la valve d'une roue de vélo.

Ou celle d'un clou enfoncé dans le pneu de la roue.

C'est la courbe suivie par un point d'un cercle qui roule sur une surface droite.

Cycloïdes: famille de courbes engendrées par un point du plan d'un cercle roulant sans frottement sur une droite ou sur un autre cercle.

Appelées aussi:

- roulettes

- trochoïdes (vieux)

- belle Hélène

- pomme de discorde

Trochoïde

La courbe décrite par un point de la roue d'un train, situé à l'extérieur du cercle de roulage sur les rails, est une trochoïde

Elle présente une zone de rebroussement; une boucle où les points présentent la particularité d'aller en arrière!

Construction de la cycloïde

Construction de trochoïde

Analytique

C'est la courbe d'équations paramétriques:

x = R ( t - sin t )

y = R ( 1 - cos t)

PROPRIÉTÉS

Dimensionnelles

Longueur	Aire
L = 8R	A = 3 R²
L = Périmètre du carré circonscrit au cercle générateur	A = 3 fois l'aire du cercle générateur
Grand diamètre
D = 2 R
D = le périmètre du cercle Normal: C'est le parcours du cercle sur la droite

Géométriques

Prenons un cercle de deux fois le diamètre du cercle générateur et, un diamètre vertical de ce cercle.

On les fait tourner l'ensemble.

Le diamètre reste tangent à la cycloïde.

C'est son enveloppe.

La développée d'une cycloïde est une cycloïde identique qui se trouve décalée d'un demi-tour par rapport à celle du départ.

Fonctionnelles

BRACHYSTOCHRONE	TAUTOCHRONE
La cycloïde est la plus rapide. La courbe le long de laquelle une bille soumise à la pesanteur se déplacera d'un point A à un point B le plus rapidement possible.	Les temps de trajets sont identiques. Quel que soit le point A de départ de la bille, elle mettra le même temps pour arriver en B .
Brachy: Brahistos: le plus court Chrone: Chronos: temps	Tauto: même Voir Identités

Tautochrone Qui a lieu dans des temps égaux.

Isochrone ou isochronique Qui s'effectue dans des intervalles de temps égaux. Les oscillations isochrones du pendule

Larousse

Le point du cercle engendrant la cycloïde prend diverses vitesses

Y compris le repos en repassant sur la droite sur laquelle roule le cercle générateur.

Dans le cas des roues du train, les points en dessous de la surface des rails parcourent des cycloïdes allongées, présentant des boucles.

De sorte que certains points de la roue repartent en arrière!

Pendules

Petites oscillations

La période du pendule ne dépend que de sa longueur

La période est constante pour un pendule de longueur donnée

Découverte de Galilée

Grandes amplitudes

Ce n'est vrai que si l'on force le pendule à s'enrouler sur une cycloïde

Du fait de sa propriété tautochrone

HISTORIQUE

Charles bouvelles - 1501 - Premières références à la cycloïde Mersenne - (1588 - 1648) - Il a formulé plusieurs problèmes à leur sujet Galilée - (1564 - 1642) - Galilée s'est posé le problème de la courbe la plus rapide – 1630 "Je cherche à décrire cette ligne courbe depuis plus de cinquante ans, car j'ai eu l'occasion d'admirer le dessin très gracieux de cette courbe pour l'adapter aux arches d'un pont" ^1 - Il pensait que cette courbe est idéale pour construire un pont: la plus robuste - Il tente de déterminer l'aire de la courbe et trouve environ 3, par pesée. Il avait vu juste! Roberval - 1634 - Il démontre que l'aire vaut trois fois celle du cercle Evangelista Torricelli - 1644 - Il écrit le premier document sur les cycloïdes - Il donne la démonstration du calcul de l'aire "À travers lesquelles, avec l'aide de Dieu, nous prouverons [que l'aire d'une cycloïde] est égale à trois fois [celle du disque qui l'a engendrée]" . Cité par Robert Ghattas – Petite salade de mathématiques. First Editions – 2005 Sir Christopher Wren - 1658 - Il démontre que le périmètre est le celui du carré circonscrit au cercle Christiaan Huygens - 1657 - Il écrit un traité du pendule synchrone, en particulier - Il tente de réaliser des pendules tautochrones avec un débattement cycloïdal; il abandonne, car compliqué à réaliser - La solution viendra: il faut placer près du point de suspension du pendule deux pièces cycloïdales qui contraignent la tige semi-rigide à parcourir elle-même une cycloïde >>> - Il imagine le système d'échappement à ancre pour réguler le rythme des horloges Pascal comme Newton, Leibniz, Bernoulli, Guillaume de l’Hopital, Jean et Jacques Bernoulli etc. - Eux aussi étudient ces courbes - Origine du calcul des variations - Utile en mécanique et en optique, puis en mécanique quantique et relativité générale

Voir aussi	Calcul des variations Carrés parfaits Cercle Chaînette Constructible Géométrie Horloge Identités Parabole Physique amusante Quadrature du cercle Sphère
Sites	Courbes : nom et particularités The tautochrone problem par Wolfram Index of /~history/curves Building and demonstrating the importance's of the Cycloid Curve – Avec video de démonstration
Cette page	http://villemin.gerard.free.fr/Construc/Cycloide.htm