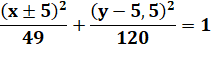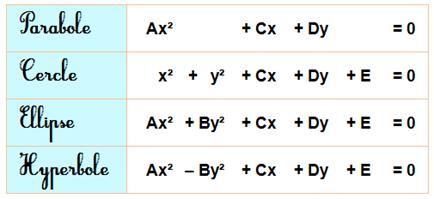NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 11/02/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométries
Débutants Géométrie	CONIQUES				Glossaire Géométrie
INDEX Courbes Géométrie	Coniques	Ellipse	Hyperbole	Parabole
		Cercle		Segment de Parabole
		Sommaire de cette page >>> Approche >>> Apollonios de Perge >>> Historique >>> Section du cône >>> Excentricité des coniques >>> Équations >>> Théorème de Brianchon >>> Dessiner les coniques >>> Vocabulaire >>> Anglais

Les CONIQUES

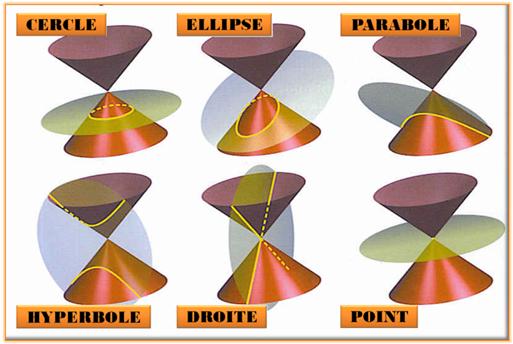
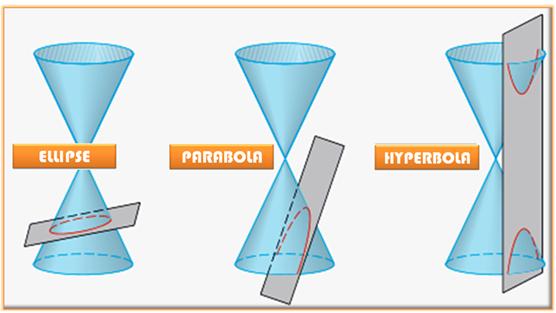
Les coniques sont des courbes obtenues par la section d'un cône de révolution par un plan. Trois coniques: ellipse, parabole et hyperbole.

Propriétés majeures qui peuvent être prises comme définitions:

ELLIPSE: ensemble* des points M tels MF + MF' = constante. Les points F et F' sont les foyers de l'ellipse.

HYPERBOLE: ensemble des points M tels MF – MF' = constante

PARABOLE: ensemble des points équidistants d'un point F et d'une droite D. Le point F est le foyer de la parabole.

*autrefois et dans ce cas, on disait: lieu.

Les planètes décrivent une ellipse autour de leur étoile. Les comètes non périodiques suivent des paraboles ou hyperboles. Les fusées ou engins spaciaux décrivent des courbes constituées de tronçons de coniques (approximation). Les télescopes à réflexion concentrent la lumière en utilisant les propriétés d'une des trois coniques (la parabole dans la majorité des cas). Le grand public connait bien les antennes paraboliques servant à capter la télévision. L'antenne d'Arecibo (écoute des émissions extraterrestres) est composée d'une parabole de 305 m de diamètre (photo).

Approche
Chacun connaît le cornet à glace en forme de cône dont l'origine remonterait à une centaine d'années. Le vendeur de glaces se trouve à court de coupelles en carton. Son voisin vendeur de gaufres lui propose une association … Voir Inventions
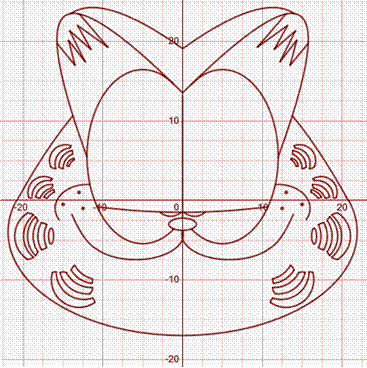
Ce dessin du chat Garfield a été créé avec des morceaux de coniques. Par exemple, les deux yeux sont des ellipses dont les équations sont:

Source de ce dessin (et bien d'autres): desmos creative art

APOLLONIUS DE PERGE vers 240 à 180 av. J.-C. - environ 82 ans
Il écrit un ouvrage de référence sur les coniques: Kônika (traité sur les sections coniques). Ouvrage qui sera restauré par Fermat sous le titre: Lieux plans d'Apollonius Apollonius analyse les sections d'un cône, et donne un nom à chaque conique: ellipse: omis => en moins; parabole: comparaison => égal, même, ce qu'il faut; hyperbole: en excès => en plus.

Voir Contemporains d'Apollonius

Historique

IV^e siècle av. J.-C. Ménechme ( -375 à – 325), élève de Platon et précepteur d'Alexandre le Grand, découvre les coniques en tentant de réaliser la duplication du cube. Un siècle plus tard dans son traité, Apollonius de Perge nommera les trois courbes: parabolé, ellipsis et hyperbolé qui signifient: "jeter à côté" à fin de comparaison, manque et excès. Johannes Werner (1468-1522), prêtre, fabricant d'instruments, adepte d'astrologie, voisin et ami d'Albrecht Dürer. Étudiant de Regiomontanus, il écrit un traité sur les coniques en 1522: Libellus super viginti duobus elementis conicis (22 théorèmes sur les coniques). Albrecht Dürer (1471-1528) en quête des secrets de la beauté, cet artiste de la renaissance s'est intéressé à la géométrie des Grecs anciens. Il est convaincu que la connaissance des mathématiques, surtout la géométrie, éviterait nombre d'erreurs dans la pratique de l'art. Il met au point une méthode de construction des coniques (entre-autres). 1525 – Instructions pour la mesure, à la règle et au compas, des lignes, plans et corps solides (Ce document passe comme le premier ouvrage important de mathématiques en allemand). Dürer commet une erreur en représentant l'ellipse comme un œuf (ovoïde). C'est Kepler (1604) qui est le premier à faire la distinction entre ovale et ellipse. Notamment en modélisant l'orbite de Mars. Girard Desargues (1591-1661) étude les coniques comme perspective du cercle; bases de la géométrie projective. Blaise Pascal (1623-1662) à 16 ans écrit un traité sur les coniques. Théorème des cinq points démontré par Pascal: par cinq points trois à trois non alignés passe une unique conique propre. L'outil GeoGebra permet le tracé d'une conique à partir de cinq points (Illustration) Les autres mathématiciens qui ont travaillé sur les coniques: La Hire, Newton, Dandelin, Gergonne, Poncelet, Brianchon, Dupin, Chasles, et Steiner. Michel Chasles (1793-1867) meilleur connaisseur des coniques à son époque. En 1864, il compte les coniques tangentes à cinq coniques du plan. Il en existe 3 264 éventuellement imaginaires. En 1997, une configuration de 3 264 coniques réelles a été construite avec cinq hyperboles. En 2005, Jean-Yves Welschinger (né en 1974) : avec cinq ellipses sans point intérieurs communs, il y a au moins 32 coniques réelles tangentes aux cinq initiales. Démontré avec exemple à l'appui. C'est le théorème de Welschinger.

Section du cône
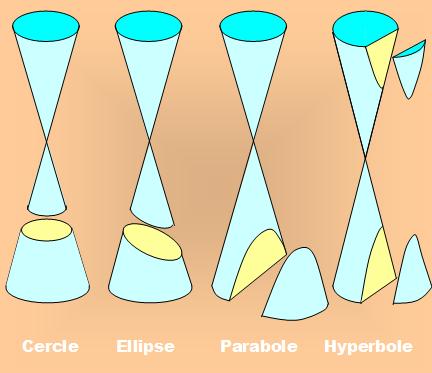
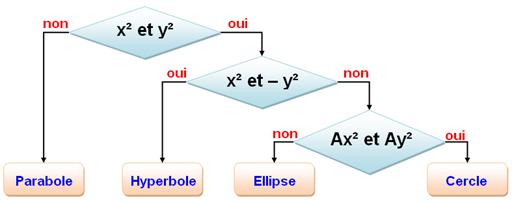
Les coniques sont des courbes planes algébriques. Selon le type de section du cône de révolution, on a: Coniques non dégénérées: Parabole, Hyperbole et Ellipse. Coniques dégénérées: Cercle, Droite et Point.	Section du cône Illustration d'après Tangente Hors-série n° 21 – L'astronomie (2005) – Page 48
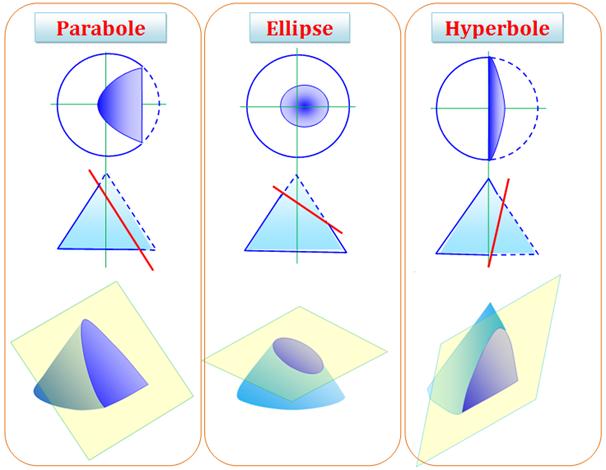
Section du cône vue du dessus, de profil et en perspective

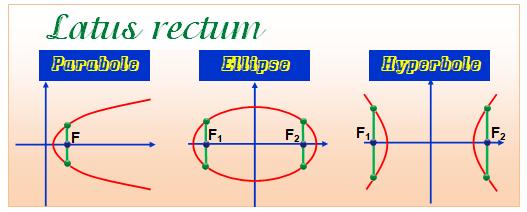
Latus rectum: segment de droite qui relie deux points d’une conique, qui est perpendiculaire à l’axe principal de la conique et qui passe par le foyer de cette conique.

Excentricité des coniques
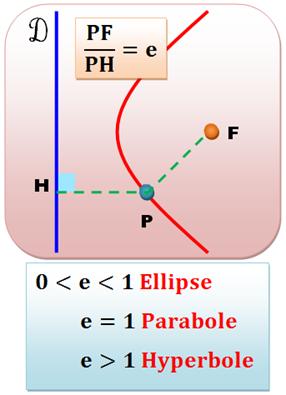
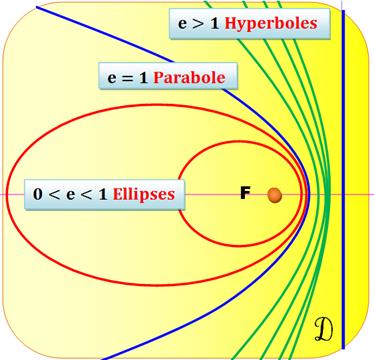
On peut définir les coniques comme le lieu d'un point se déplaçant dans un plan tel le rapport de sa distance à un point fixe F (le foyer) à la distance à une droite fixe (la directrice) est une constante. Ce rapport est l'excentricité (e) de la conique (anglais: eccentricity). Excentricité Les coniques peuvent être définies et distinguées par leur excentricité (eccentricity). Une droite D, dite directrice; Un point fixe F, dit foyer; Un point P situé sur la conique; La distance PH du point P à la droite D (PH est perpendiculaire à D); La distance du point P au foyer F; et C'est rapport entre ces deux distances qui est baptisé excentricité.
Définition des coniques	Exemples

Dessiner des coniques
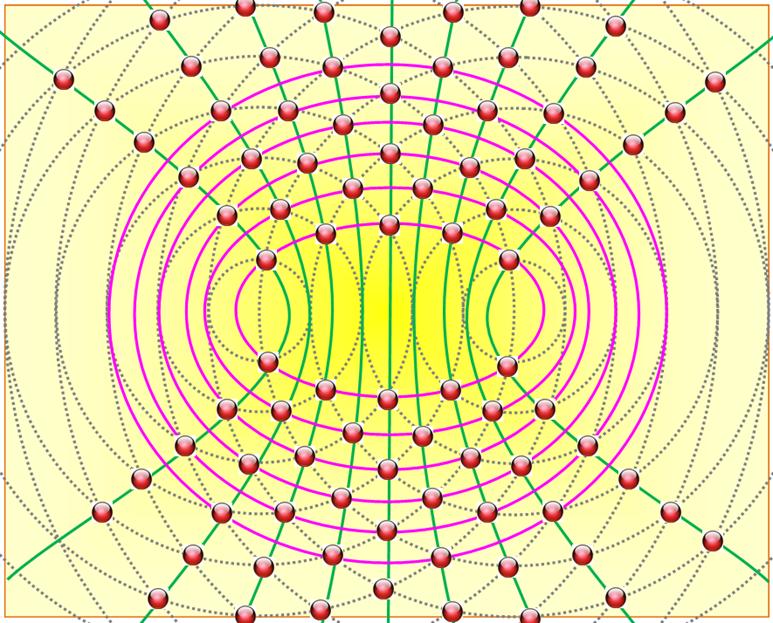
Deux jeux de cercles concentriques (gris pointillés) dont les centres sont espacés. Alors les intersections (billes rouges) sont situés sur, à la fois: une série d'ellipses (roses) et une série d'hyperboles (vertes) Ces coniques, ellipses et hyperboles, sont mutuellement orthogonales. Deux jeux de paraboles de même foyer, mais de sens opposés, sont également mutuellement orthogonales (ci-contre).

Théorème de Julien Brianchon (1785-1864)
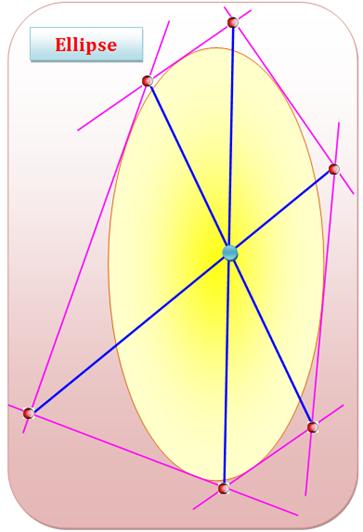
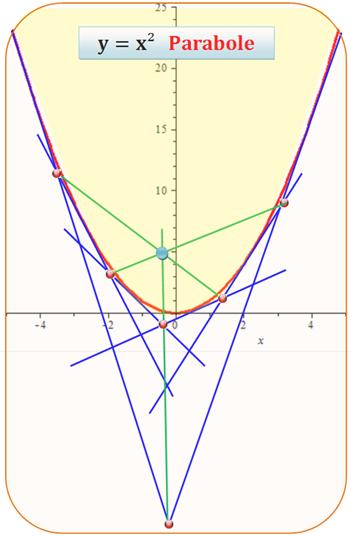
Une conique et six tangentes; leurs points d'intersection (billes rouges). Les droites reliant les paires de points opposés sont concourantes.

Voir Étoile mystérieuse de Pascal / Théorème de Pappus / Ellipse et ses curiosités

Équations
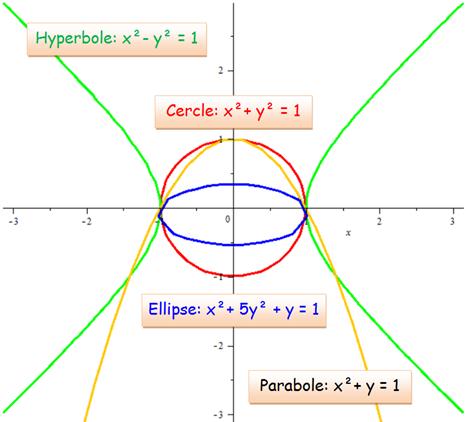
Équations des coniques Leur équation est de forme quadratique (second degré): Algorithme de caractérisation de la conique selon l'équation Exemples Programme correspondant (Maple) Œil de Garfield Les deux équations de l'ellipse dessinant les yeux de Garfield: Cette équation en Ax² + By² (x et y sont au carré et tous deux de même signe) est bien celle d'une ellipse.

Vocabulaire des coniques
Section conique	Conic section	Courbe issue de la section d'un cône.
Cône circulaire droit ou cône de révolution	Right circular cone	Cône dont la base est un cercle et dont la perpendiculaire en son centre passe par le sommet (axe du cône).
Centre	Center	Centre du cercle, de l'ellipse ou de l'hyperbole.
Sommet	Vertex, vertices	Parabole: point de rebroussement. Ellipse: extrémités du grand axe. Hyperbole: point d'inflexion sur une branche de l'hyperbole.
Foyer	Focus, foci	Un point à partir duquel est mesurée la distance définissant la conique. Point de convergence de toutes les droites définissant la distance.
Directrice	Directrix, directrices	La droite à partir de laquelle la distance est mesurée pour définir la conique.
Axe	Axis, axes	La droite perpendiculaire à la directrice passant par le sommet de la parabole. Axe de symétrie.
Axe principal ou axe focal	Major Axis Semi-major axis Horizontal radius	Ellipse: ligne joignant les foyers. Elle est perpendiculaire à la directrice. Les demi-droites issues du centre sont les demi-grands axes
Axe secondaire	Minor Axis Semi-minor axis Vertical radius	Médiatrice du grand axe. Les demi-droites issues du centre sont les demi- axes secondaires
Ensemble de points ou lieu des points	Set of points or locus, loci	Il définit les conditions d'appartenance à la conique.

Voir Vocabulaire des mathématiques

English corner
A conic section (or just conic) is a curve obtained as the intersection of a cone (more precisely, a right circular conical surface) with a plane. Conic sections are the curves which can be derived from taking slices of a "double-napped" cone. (A double-napped cone, in regular English, is two cones "nose to nose", with the one cone balanced perfectly on the other.)

Suite	Ellipse Étoile mystérieuse de Pascal Théorème de Pascal Problème des trois cercles
Voir	Cercle Cône Courbes élémentaires DicoMot Équation des coniques Géométrie – Débutants Géométrie – Glossaire Géométrie – Index Hyperbole Parabole Sphère Théorème de Pascal
Livre	Des courbes célestes par Jacky Couvret –Tangente Hors-série n° 21 – L'astronomie (2005) – Pages 48 à 53
Sites	Les coniques – Robert FERRÉOL, Jacques MANDONNET Les coniques – Serge MEHL Les coniques – Applets par XiTi Les coniques – Bibm@th Les coniques – Simples par M@ths et tiques
Cette page	http://villemin.gerard.free.fr/Geometri/Coniques/Coniques.htm