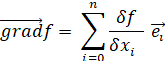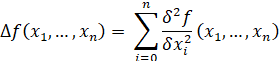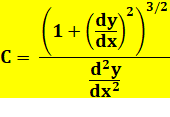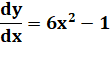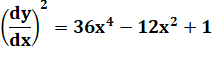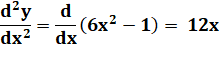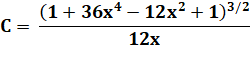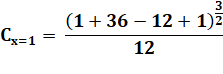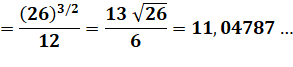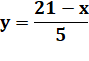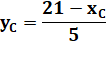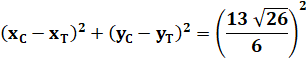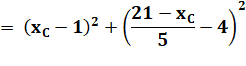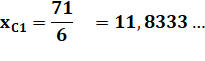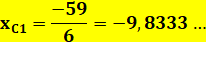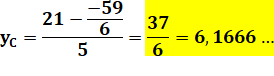|
|||||||||||||||||||||||||||||||||||
![]()
|
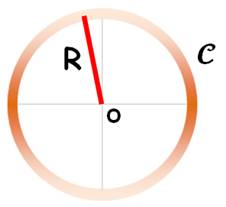
COURBURE Rayon de courbure Appréciation
de la nature d'une courbe, d'une surface, d'une variété. Notion de virage, de sinuosité, de creux, de bosses … |
Anglais : Curvature radius
|
|
||
|
|
Droite
Courbure nulle Cercle
Courbure
constante 1/R Courbe
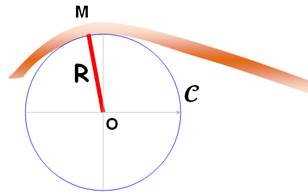
Courbure
variable: 1/R en
M |
|
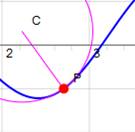
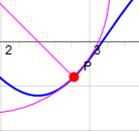
Une idée du rayon de courbure
|
|
Voir Animation sur la page
de M. Bourne
|
|
||||||||||||||
|
|
||||||||||||||
|
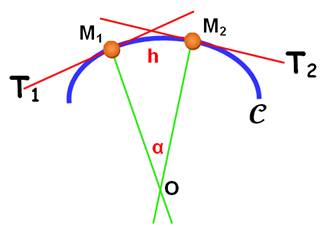
Les perpendiculaires à ces deux tangentes. L'angle
Un vecteur dans la direction
MO lui est associé à la courbure. |
Note: Pour le cercle, cette définition est cohérente avec celle de la mesure
des angles en radians:
|
|||||||||||||
|
Bilan
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
La conjecture de Poincaré a été démontrée
en utilisant de tels outils: le flot de Ricci. Notion
avancée (pour information seulement) Tout étudiant en licence aura à se familiariser
avec ces notions …
|
|
![]()
|
Rayon de courbure sur
courbes définies |
|
|
|
Le rayon de courbure en un point donné
de la courbe définie par y = f(x) est donné par la formule => |
Voir Démonstration
(anglais) |
|
|
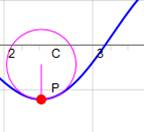
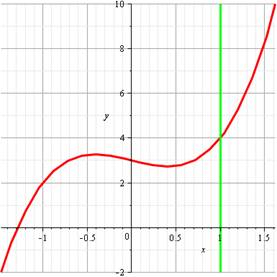
Exemple: trouvez le rayon de courbure en x = 1 de
=> |
y = 2x3 – x + 3 Pour
x = 1, y = 2 – 1 + 3 = 4 |
|
|
Allure du graphe => Dérivées
Voir Dérivées |
|
|
|
Calcul de la courbure |
|
|
|
Et sa valeur en x = 1 |
|
|
|
Coordonnées du centre du cercle osculateur |
|
|
On connaît un point du cercle: |
T (1,
4) |
|
La pente de
la tangente: |
dy/dx =
6x² - 1, soit
pour x= 1: m = 5 |
|
La normale à cette tangente, un
rayon du cercle: |
p = –
1/5 |
|
Équation de la
droite portant ce rayon: |
y – y1
= m (x – x1) y – 4 =
-1/5 (x – 1)
|
|
Ordonnée du centre: |
|
|
Distance centre au point de tangence
= rayon de courbure: |
|
|
Résolution de l'équation du second
degré: |
|
|
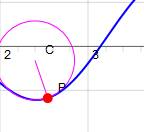
Valeur de x avec la racine négative
(cf. allure de la courbe) |
|
|
|
|
|
We can draw a circle that closely fits nearby points on a local
section of a curve. We say the curve and the circle osculate
(which means "to kiss"), since the two curves have the same tangent
and curvature at the point where they meet. The radius of curvature of the
curve at a particular point is defined as the radius of the approximating
circle. This radius changes as we move along the curve. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Bande dessinée |
Une
vulgarisation de la topologie en bande dessinée écrite par Jean-Pierre Petit |
|
Livre |
|
|
Sites |
|
|
Cette page |
![]()