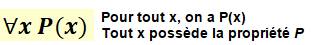![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page |
|
22 Novembre 2025
![]()
|
Édition du: 29/11/2025 |
|
INDEX lettre A |
Dictionnaire de base du vocabulaire des mathématiques |
|
|
Faites
un double-clic pour un retour en haut de
page
Pour
trouver un mot: Ctrl F et tapez le mot
cherché
|
Avertissement Dictionnaire pour débutants,
juniors, novices, "nuls" … !!! On privilégie la compréhension par rapport à une rigueur mathématique !!! Les liens permettent de compléter et d'approfondir Pour une
version plus académique se reporter aux ouvrages spécialisés |
Légende Parfois,
plusieurs définitions sont données: de la plus "intuitive" à la
plus correcte mathématiquement Mode de recherche: si vous ne trouvez
pas symétrie centrale à symétrie, voyez à centrale, par exemple. Difficulté: * notion avancée;
** notion complexe. |
![]()
A à l'envers: ![]() signifie: quelle que soit la valeur de a ou,
pour toute valeur de a.
signifie: quelle que soit la valeur de a ou,
pour toute valeur de a.
– symbole appelé quantificateur
universel.
![]() – étym. du mot allemand alle qui signifie tout.
– étym. du mot allemand alle qui signifie tout.
– v. Quantificateurs
– a.
universal quantifier, se dit: all
Abaisser une
perpendiculaire: veut dire dessiner une
droite à 90° de l'autre.
Aujourd'hui on dit plus simplement: tracer une perpendiculaire.
– v. Élever, construire une
perpendiculaire
– a. Construct (or draw) a
perpendicular line
Abaisser le degré d'une équation*: ramener une équation à un degré
inférieur pour faciliter sa résolution. Par exemple pour une équation du quatrième degré du type ax4
+ bx2 + c = 0, poser y = x² et la nouvelle équation descend au deuxième degré.
– a. Reducing the degree of an equation, of a polynomial
Abaque (un -): dessin, diagramme
dont la lecture permet de connaître directement une solution à un problème de
calcul numérique:
Abaque à calculer: cadre à tiges sur lesquelles
circulent des boules trouées qui servent à calculer.
– histo. table puis tablette
servant à calculer à l’aide de cailloux ou de jetons, puis de boules coulissant
sur des tiges.
– syn. existe aussi comme synonyme de boulier.
– v. Boulier, nomographie
– a. Nomogram or abaque
Abélien (groupe -)* synonyme de commutatif pour les groupes.
– v. Groupe, vocabulaire
des structures algébriques
– a. Abelian group or
commutative group
Abondance (taux d'-): somme des diviseurs
rapportée au nombre lui-même. Deux nombres partageant le même taux d'abondance
sont amis.
– v. Fonctions arithmétiques
– a. Abondancy
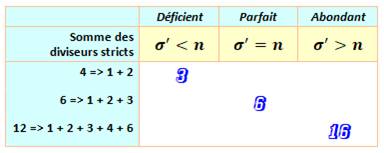
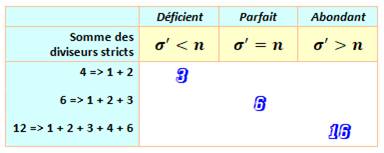 Abondant: se dit d'un nombre entier naturel dont la
somme des diviseurs stricts est supérieure au nombre
lui-même.
Abondant: se dit d'un nombre entier naturel dont la
somme des diviseurs stricts est supérieure au nombre
lui-même.
Exemple: la somme des diviseurs stricts de 12 (1, 2, 3, 4, 6) est 16, nombre
strictement supérieur à 12. le nombre 12 est abondant.
En cas d'égalité, le nombre est parfait; plus
petit, il est déficient.
– a. Abundant, deficient and
perfect numbers. An abundant number or excessive number is a number
for which the sum of its proper divisors is greater than the number
Abscisse:
valeur
(coordonnée) lue sur la ligne
horizontale (x) d'un repère; adresse horizontale d'un point dans un repère xy.
L'ordonnée est en vertical.
D'une manière générale, l'abscisse est une des coordonnées pour repérer un
point sur une droite, sur un plan, dans
l'espace.
– proches: Abscisse, ordonnée, cote
– v. Coordonnées
Abscisse à l'origine: zéros
d'une fonction f(x).
Points de rencontre de la courbe représentant f(x) avec l'axe des x.
Abscisse angulaire et abscisse curviligne: longueur d'arc et angle
orienté
– v. Abscisse angulaire et
curviligne
Absolue (valeur -): nombre sans son
signe (donc positif)
– notation: ![]() ou abs(-6) = abs(+6) = 6
ou abs(-6) = abs(+6) = 6
– v. Module, opposé
– a. Absolute value, magnitude
Absolu (zéro -) : 0 Kelvin = 273,15
°C.
Impossible de descendre plus bas en température. État tel que l'agitation des
molécules est nul.
–
v. Température limite
– a. Assolute zero
Le
zéro absolu1,2 est la température la plus basse qui puisse exister. Il
correspond à la limite basse de l'échelle de température thermodynamique, soit
l'état dans lequel l'enthalpie et l'entropie d'un gaz parfait atteint sa valeur
minimale, notée 0.
Absolute zero is the
lowest limit of the thermodynamic temperature scale, a state at which the
enthalpy and entropy of a cooled ideal gas reach their minimum value, taken as
zero kelvin.
Absorbant ou permis: L'élément
absorbant de la multiplication est 0, car 0 x n = n x 0 = 0.
Soit un ensemble E muni d'une loi de composition notée * ; un élément a de
E est dit absorbant à droite, respectivement à gauche, si, pour tout élément x
de E on a : a * x = a ou x * a = a.
Sans autre indication, il est absorbant des deux côtés.
S'il existe dans un ensemble, il est unique.
– ex. Dans
l'ensemble des parties d'un ensemble E : P(E) muni de la loi intersection,
l'ensemble vide Ø est l'élément absorbant. En effet, pour tout X de E : X ∩
Ø = Ø ∩ X = Ø.
– a. Absorbing element or
annihilating element
Abstraction: processus cognitif
(opération intellectuelle) qui permet d'isoler des choses par la pensée. À la
base, la formation d'un concept qui permet de regrouper les objets selon un
élément commun. Ce concept apparaît en tant que résultat d’un processus qui met
de côté certaines choses : la couleur, la taille, la forme, etc. Capacité à
conceptualiser et à faire des comparaisons. Le nombre 5, caractérisant
toute collection de cinq objets, est une abstraction. Les opérations arithmétiques avec
leurs symboles sont des abstractions.
– a. Abstraction
Absurde:
contraire
à la raison, à la logique
– étym. du latin absurdus,
discordant, absurde
– v. Contradictoire, tiers exclu
– a. Absurd, nonsense
Absurde (démonstration par l'-,
raisonnement ar -) ou apagogie: on fait une hypothèse
fausse, on démontre qu'elle conduit à une propriété manifestement fausse, donc
l'hypothèse est à rejeter, elle est fausse.
Pour démontrer qu'une proposition A est fausse, on suppose qu'elle est vraie et
on montre que cela conduit à une conclusion incompatible avec l’hypothèse de
départ.
– v. du latin reductio ad absurdum
– v. Raisonnement, Démonstration par l'absurde, Racine
de 2 est irationnel
– a. Reductio ad absurdum: form
of argument that attempts to establish a claim by showing that the opposite
scenario would lead to absurdity or contradiction.
Abus de langage ou
omission volontaire: forme simplifiée qui allège la formulation sans
créer d'ambiguïtés. De même nature que lorsqu'en français on dit "boire un
verre" au lieu de "boire le contenu d'un verre".
Stella Baruk cite le cas
suivant: "la somme des chiffres d'un nombre" au lieu de "la
somme des nombres représentés par les
chiffres" car un chiffre est
un signe et non un nombre.
On dira souvent sans que cela gêne: "un segment de 3 cm" au lieu de
"un segment qui mesure 3 cm" ou "un segment de longueur 3
cm".
– a. The term is often
mistakenly; Through linguistic evolution, we have come to use the word …
Accélération: l'accélération est une modification
de la vitesse par rapport au temps; c'est la dérivée de la vitesse par
rapport au temps
–
v. Accélération
– a. Acceleration.
Accolade: { }
–
a. Brace
Accouplement ou couplage: mise en relation de deux
entités
Application bilinéaire
– a.
Pairing
Accroissement: différence entre deux valeurs de la
fonction pour deux abscisses données.
Soit f une fonction réelle de la variable réelle. Si x0 et X1
sont deux valeurs de cette variable telles que f(x0) et f(x1)
existent, on appelle accroissement de la variable le nombre réel positif ou
négatif x1 – x0 et accroissement correspondant de la
fonction le nombre réel f(x1)
– f(x0).
– a.
Increase, growth
Théorème des accroissements finis (TAF):
pour toute droite sécante en deux points à une courbe différentiable, il
existe, entre ces deux points, une tangente parallèle à la sécante.
– ex. si un véhicule
parcourt une distance à la vitesse moyenne de 60 km/h,
alors son compteur a indiqué au moins une fois la vitesse précise de 60 km/h.
– a. Mean value theorem
Accumulation (point d'-
)*: en topologie, un point qui, en un certain sens, est collé à une partie
d'un espace topologique.
Une partie A d'un
espace topologique E. Un point x de cette partie est point d'accumulation de A
si tout voisinage de x contient au moins un point de A autre que x.
– a. Limit point, accumulation point, or cluster point
Acquisition comprimée: procédé mathématique
"réalisant" la compression de données, et cela à la source.
– v. Mathématique de la parcimonie, compression de
données
–
a. Data compressed entry
Actif: dans un bilan, colonne de nombres qui
témoignent de l'emploi des ressources de l'entreprise; ex: la vente d'un
produit manufacturé qui se conclut par une facturation, donc un paiement est
une ligne de la colonne de l'actif.
Mnémo: le fait d'utiliser l'argent
(les fonds de l'entreprise) est une opération active qui débouche sur
des activités.
–
v. Passif, débit, crédit
– a. Assets = actif; Balance sheet = bilan; liabilities and owner's
equity = passif
Action de groupe**: une action d'un groupe sur
un ensemble est une loi
de composition externe du groupe sur l'ensemble, vérifiant des conditions
supplémentaires.
On dit que le groupe G opéré sur l'ensemble E.
– ex.
la permutation est une action de groupe parmi de nombreuses autres.
L'orbite
de x de E est l'ensemble des éléments de E associés à x sous l'action de G. La
relation y est dans l'orbite de x est
une relation d'équivalence sur E. Les classes d'équivalence sont les orbites.
En particulier, les orbites forment une partition de E.
– v. Quart de
tour, morphisme
– a.
Group action
Acutangle (triangle -):
triangle
qui a trois angles aigus.
– ancien: oxygone
– v. Triangle
acutangle, triangle
obtusangle, partition
de l'obtusangle en acutangles
– a. Acute triangle
Addition:
opération qui consiste à ajouter, à mettre tous les objets
ensemble et à compter la quantité totale.
Opération binaire qui associe à deux nombres a et b, appelés termes, leur somme est le résultat de a + b. Lecture a plus b; dans le langage
courant le "et" associant deux
quantités se traduit souvent par le signe "+".
Ex: j'ai deux chats et trois chiens, ce qui fait cinq animaux. 2 + 3 = 5.
– syn. ajouter, augmenter, incrémenter
– v. Addition, partition
– a. Addition
Addition (définition formelle):
Soit A et B deux ensembles disjoints dont les cardinaux sont respectivement m
et n, par définition, le cardinal de la réunion
A U B est appelé la somme des deux cardinaux m et n ; elle est
notée m + n.
Les cardinaux m, n et m +n sont des nombres entiers naturels.
La loi de composition interne ainsi définie dans N est appelée addition. Elle
est commutative et associative ; elle est telle que 0 est l'élément
neutre.
Généralisation : On appelle addition toute loi de composition interne
commutative et associative dans un ensemble E. Le composé de deux éléments x et
y est noté x+ y, somme des deux éléments.
Addition de fractions: faisable que si les fractions sont d'abord réduites
au même dénominateur, alors on ajoute les numérateurs.
– v. Addition de
fractions, réduction
au même dénominateur
– a. Adding fractions, common denominator method, make the denominators the
same
Addition de vecteurs: Avec les deux
vecteurs à additionner, translatez-les pour avoir la même origine, puis formez
un parallélogramme. La diagonale orientée issue de l'origine est la somme des
deux vecteurs.
– v. Addition de vecteurs
– a. Vector addition, adding and
subcontracting vectors. The sum of two or more vectors is called the resultant.
The resultant of two vectors can be found using either the parallelogram method
or the triangle method .
Addition de matrices: n'est possible
qu'avec deux matrices
de même dimension.
Alors chaque nouvel élément est la somme des deux éléments homologues.
– a. Adding matrice; the sum of matrices is obtained by adding the
corresponding elements.
Additionner: synonyme d'ajouter,
de faire une addition.
Incrémenter, c'est ajouter une valeur fixe à une variable, souvent 1.
– a. At school, the child learns to add numbers; It easy to add up quantities
of a very different nature
Addend: anglais pour terme d'une addition. Any of the numbers that are added together. Example: In 8 + 3 = 11, the 8
and the 3 are addends.
Adhérence**: Un point x est
adhérent à un ensemble A inclus dans un espace topologique
E si tout voisinage de x rencontre A. L'adhérence de A notée ![]() est l'ensemble des points adhérents à A. On
l'appelle aussi fermeture. L'adhérence de A, c'est aussi le plus ensemble fermé
contenant A. Ex: l'ensemble des réels
est l'ensemble des points adhérents à A. On
l'appelle aussi fermeture. L'adhérence de A, c'est aussi le plus ensemble fermé
contenant A. Ex: l'ensemble des réels
![]() est l'adhérence de l'ensemble des rationnels
est l'adhérence de l'ensemble des rationnels ![]() .
.
– a.
Point of closure or adherent point
Adjacents (angles -): des angles
adjacents ont un sommet et un côté commun,
chacun d'eux est situé de part et d'autre du côté commun
– v. Angles, angle intérieur et angle extérieur
– a. Adjacent angles
Adjacents (segments -): des segments adjacents ont une extrémité commune; une suite
de segments adjacents forme une ligne brisée ou ligne polygonale.
Adjacents (côtés -): côtés qui ont un sommet commun dans un polygone.
– a. Adjacent sides
Adjacentes (faces -): faces qui ont une
arête commune dans un polyèdre.
– a. Adjacent faces
Adjacents (sommets -): sommets connexes (voisins) dans un graphe.
– a. Adjacent vertices
Adjacentes (suites -)**: deux suites réelles
(an) et (bn) sont dites adjacentes si l'une des suites
est croissante (au sens large), l'autre suite décroissante (au sens large) et
si la différence des deux converge vers 0.
– a. Adjacent sequences
Adjacent (topologie): parties adjacentes d'un espace topologique: leurs
frontières ont au moins un point commun et aucune des deux parties n'a de
points à l'intérieur de l'autre.
Adjectif numérique
ordinal: tous les adjectifs formés sur les nombres donnant un rang: premier,
deuxième …
– v. Ordinaux
– a. Cardinal numbers are counting numbers. Ordinal numbers are numbers that tell
you the position of someone or something in a group or list. Ordinal numbers
tell order.
Affine:
mot
un peu étrange (venant de "affinités") pour dire grosso modo "linéaire".
Selon Euler, lorsqu'on change x en ax et y en by, les courbes demeurent
semblables si a = b, elles ne le sont plus si a est différent de b, mais elles
ont entre elles de l'affinité.
– v. Affine
– a. Affine
Affine (application ou fonction
-): relation qui a chaque nombre x associe une nombre
ax + b, a et b étant deux nombres connus; fonction ![]() dont la représentation est une droite; une
fonction linéaire est une fonction affine pour laquelle b = 0
dont la représentation est une droite; une
fonction linéaire est une fonction affine pour laquelle b = 0
Affine (espace -): espace le plus
basique dans lequel aucun point n'est privilégié; en définissant la notion de
distance, on passe de l'espace affine à l'espace euclidien, qui est l'espace de
notre géométrie classique à l'école;
Affine (géométrie -): géométrie des
propriétés invariantes par des transformations
du premier degré (linéaire).
La géométrie affine est ce qui reste de la géométrie
euclidienne lorsqu'on ignore les notions de mesures de distance et d'angles. La
notion de droites parallèles est indépendante de toute métrique. La géométrie
affine est souvent considérée comme l'étude des droites parallèles.

Affinité: transformation
suivante: à chaque point M du plan correspond un point M' tel que PM' = k . PM
(en vecteurs).
Elle est définie par deux droites D et D' non parallèles et un coefficient réel
k.
P est l'intersection avec D d'une parallèle en M à D'. Les vecteurs sont
orientés dans la direction de D'
Affirmation: proposition, vraie ou fausse.
– v. Logique formelle, contradiction
– a. Statement: a meaningful
declarative sentence that is true or false,
Affixe (une -): coordonnées
d'un point du plan donnée par sa notation complexe z = a + ib.
– v. Nombre complexe
Agrandissement:
synonyme
de grossissement; zoom-avant.
Homothétie: toutes les dimensions de la
figure sont multipliées par un facteur k
supérieur à 1, le coefficient d'agrandissement; la figure de départ et la
figure agrandie sont semblables et k est le rapport
de similitude.
– v. Homothétie, échelle,
réduction, dilatation
– a. Expansion, enlargement
Aigu (angle -): angle de moins de
90°. En fait > 0° et < 90°.
– v. Angles:
droit, aigu, obtusangle …
– a. Acute angle: 0 to 90° in measure
Aire: mesure de la
surface; quelle est la grandeur de la surface, son étendue?
L'aire du carré
est égale à ![]() ; celle du disque à
; celle du disque à ![]() ;
;
Elle s'exprime en mètres carrés (m²) ou ses multiples (km² …)
ou sous-multiples (cm², mm²…)
– v. Aire, périmètre, superficie, volume.
– a. Area
Aire
d'un solide: somme des aires des faces du
solide.
– a. The surface area of a solid object is a measure of the total area
that the surface of the object occupies.
Aire latérale d'un solide: somme des aires des
faces latérales de certains solides comme les
prismes, les pyramides ou les cylindres.
– a. Lateral area of a cone, a cylinder, a pyramid …
Ajouter: synonyme de additionner
Ajustement
affine ou droite de régression ou droite de tendance: droite tracée sur
un nuage de points dont la répartition à une tendance linéaire (affine) de
manière à le représenter au mieux.
– v. Droite de régression, régression
linéaire
– a. Linear trend estimation
al. (et
al.): locution utilisée pour tronquer une listes, généralement de personnes. On
annonce l'auteur principal puis et al. au lieu de citer tous les
collaborateurs.
–
étym. du latin alius, autres.
Aléatoire: qui est dû au
hasard; qui dépend d'événements incertains.
Se dit d'une expérience dont l'observateur est dans l'impossibilité de prédire
le résultat.
– ex. Fonction aléatoire, variable
aléatoire
– syn. Hasard, pseudo-aléatoire
– v. Hasard, jeux de hasard, jeux de dés, probabilités,
stochastique, probabilités et
statistiques
– a. at random, au hasard; unpredictable
Aléatoires (nombres -)** impossible de prédire
quel chiffre viendra après l'autre; Avec
de telles données, un programme de compression
serait inefficace; nombre tel que pour passer de n chiffres à
n+1, il est impossible de réduire la complexité du nombre;
précision: aléatoire au sens de Per Martin-Löf et
complexe au sens de Kolmogorov
– v. Oméga
Générateur de nombres aléatoire: dispositif
(programme) capable de produire une suite de nombres pris au hasard. Aucune possibilité
connue de déterminer une logique pour prédire l'un connaissant les autres.
Un tel générateur est quasiment impossible à réaliser, on parle plutôt de
générateurs de suites de nombres pseudo-aléatoires.
–
v. Comment saisir le
hasard
– a. Random number generator
Aléatoire (échantillon -)** : sous-ensemble d'événements résultant d'un tirage
aléatoire.
– v. Tirage de trois boules dans une urne opaque.
–
a. Random sample, simple random simple
Aléatoire (variable -)** : La fonction
décrivant les valeurs possibles d'une variable aléatoire et leur probabilité
est connue sous le nom de loi de probabilité ou
de distribution de probabilité.
– a. Random variable, stochastic variable
Aleph (א)* première lettre de
l'alphabet hébreux.
Cardinal
des ensembles infinis; il y une même infinité de nombres entiers, de nombres pairs, de
nombres impairs … mais il y une infinité "plus grande" de nombre réels.
Le monde des infinis ou transfinis est
particulièrement paradoxal !
Aleph 0 est le cardinal de N (ensemble
des nombres naturels).
Aleph 1 est celui de R (ensemble des nombres réels)..
– v. Aleph et infinis, diagonale de Cantor,
hypothèse du continu,
Brève 101
– a. Aleph number
Alexandrin:
en poésie, vers de douze syllabes, divisés en deux moitiés dites hémistiches.
– étym. Poème français su
Alexandre le Grant vers 1177
– v. Poésie
– a. Alexandrine: a line of poetic meter having twelve syllables, usually
divided into two or three equal parts.
Algèbre:
branche
des mathématiques ayant pour objet de résoudre, au moyen d’équations,
des problèmes où les grandeurs sont représentées par des symboles abstraits.
Ainsi, l’opération "addition" s’écrira "a + b".
Étude
des opérations
sur les nombres,
remplacés par des lettres, et mise en évidence de leurs structures;
généralisation de l'arithmétique
à d'autres éléments mathématiques que les nombres.
– étym. mot qui vient de
l'arabe Al Jabr, remplir, réduire une
fracture.
– v. Algèbre, techniques
de base de l'algèbre, théorème fondamental de
l'algèbre
– a. Algebra
Généralisation de l'arithmétique en
remplaçant les nombres par des lettres.
Ce fut un premier pas vers l’abstraction, un
progrès considérable qui fut accomplis lorsque les mathématiciens ont pris la
liberté de remplacer des nombres par des lettres ou des symboles et qu’ils ont
appris à calculer sur ces objets : l’algèbre venait de naître...
Partie des mathématiques dont l'objet, au
départ, était l'étude des opérations sur les nombres entiers, rationnels, réels
ou complexes. Par la suite, études de lois de composition entre éléments d'un
ensemble, et pas nécessairement les nombres ; et étude de structures
algébriques comme les groupes,
anneaux, corps, etc.
Algébrique (nombre-): nombre racine d'une
équation algébrique (ou
polynomiale) à coefficients entiers (ou fractionnaire); nombre réel ou complexe non-transcendant.
Ce sont tous les nombres sauf les transcendants.
– ex. le nombre d'or, (1+√5)/2, est un nombre algébrique car racine de
x² – x – 1.
– v. Nombres algébriques, polynôme, racine
– a. Algebraic number: an algebraic number is a number that is a root of a
non-zero polynomial in one variable with integer (or, equivalently, rational)
coefficients.
Algébrique (mesure -): soit deux points A
et B situés sur un axe Ox. On appelle mesure algébrique du segment AB et on
note le nombre réel égal la différence
entre l’abscisse de B et celle de A: = xB - xA.
Si A, B, C sont trois points d’un même axe, les mesures algébriques de AB, de
BC et de CA sont liées par la relation : ![]() . C'est la relation de Chasles.
. C'est la relation de Chasles.
Algébrique (structure -)*: notion qui vise à
classer les objets mathématiques à partir de propriétés qui les représentent
tous.
Généralisation des notions de calcul ordinaire à des calculs plus abstraits.
– ex. Un ensemble
d'objets (comme les nombres) et une opération (comme l'addition) permet de
définir un groupe. Tout type d'objet avec cette opération partagera des
propriétés communes comme la transitivité.
– v. Groupe / Structures
algébriques
– a. Algebraic structure
Un ensemble E a une structure d'algèbre sur
le corps K (K-algèbre) s'il est muni de trois lois de composition : deux
lois de composition interne (l'une notée + et l'autre *) et une loi externe (notée ●), satisfaisant aux
conditions suivantes :
![]() E
muni des lois + et ● est un espace
vectoriel sur K ;
E
muni des lois + et ● est un espace
vectoriel sur K ;
![]() La
loi * est distributive par rapport à loi
+ ;
La
loi * est distributive par rapport à loi
+ ;
![]() Pour
tout couple (λ, µ) d'éléments de K et tout couple (x, y) d'éléments de E,
on a ; (λ●x) * (µ●y) = ( λ●µ) * (x●y)
Pour
tout couple (λ, µ) d'éléments de K et tout couple (x, y) d'éléments de E,
on a ; (λ●x) * (µ●y) = ( λ●µ) * (x●y)
Si la loi * est associative (donc, si E muni
de + et * est un anneau), l 'algèbre est dite associative ; si la loi
* est commutative, l'algèbre est dite commutative.
Algèbre (une - )** structures
algébriques qui comportent deux lois de
composition interne et une externe.
Une K-algèbre est une algèbre sur un corps commutatif
K de structure algébrique (A, +, ·, ×)
telle que :
![]() (A,
+, ·) est un espace vectoriel sur K ;
(A,
+, ·) est un espace vectoriel sur K ;
![]() la
loi × est définie de A × A dans A (loi de composition interne) ; et
la
loi × est définie de A × A dans A (loi de composition interne) ; et
![]() la
loi × est bilinéaire.
la
loi × est bilinéaire.
Algèbre linéaire: étude des transformations
linéaires, des systèmes d'équations
linéaires, des espaces vectoriels.
– a. Linear algebra
C’est l’étude d’un ensemble muni d’une
structure algébrique particulière appelé espace vectoriel. Cette structure a
une représentation tellement évidente dans l’espace dans lequel nous vivons
qu'elle est devenue un domaine a part de l’algèbre. Il permet d’aborder d'une
façon nouvelle la géométrie euclidienne. Les propriétés géométriques
familières, telles que le parallélisme de deux droites par exemple, se trouvent
résolues d’une façon axiomatique et algébrique. Dans ce cas, les démonstrations
de ces propriétés géométriques peuvent se passer d’une représentation imagée et
se résolvent par des propriétés algébriques uniquement.
Algèbre de Boole: algèbre de la
logique.
Étude des relations logiques, et dans laquelle les opérations de réunion,
d'intersection et de complémentation expriment respectivement la disjonction,
la conjonction, la négation logiques
– v. Algèbre de Boole, opérateurs ET, OU, etc. La logique en bref
George Boole (1815-1864) publie Analyse mathématique de la logique
(1847) et Étude des lois de la pensée.
Il fonde la logique mathématique.
Idée : repérer certaines fonctions
caractéristiques dans notre langage ordinaire, de façon à pouvoir les traduire
dans les termes d’une algèbre symbolique et identifier dans celles-ci des lois
de calcul qui deviendront la forme mathématique des lois de la pensée.
Base : une proposition est un énoncé qui
est vrai ou faux, notée 0 ou 1.
Algèbre extérieure** ou de Grassmann: introduit la
multiplication de vecteurs de
manière à calculer le volume des solides de dimensions
n (parallélotopes, parallélogrammes généralisés aux dimensions supérieures).
Une algèbre qui permet de travailler sur des hyper-volumes, en calcul différentiels
comme dans la recherche de l'infini.
– a. Exterior algebra or
Grassmann algebra
Algorithme: pensez à recette,
comme une recette de cuisine.
Un algorithme est une suite de règles,
d’instructions, qui une fois exécutée correctement et dans un ordre précis,
conduit à un résultat donné.
L'algorithme doit contenir uniquement des instructions compréhensibles par
celui qui devra les exécuter.
Séquence
d'opérations arithmétiques et logiques permettant de résoudre mécaniquement un
problème en une suite d'étapes en nombre fini.
La suite d'opérations traduite en langage ordinateur constitue un programme.
L'intérêt est qu'un algorithme fonctionne quelles que soient les données
d'entrée.
– étym. d'Algorismus
latinisation d'al-Khuwârizmi, célèbre
mathématicien arabe
– v. Algorithme, logiciel, ordinateur /
Programmation, programmes sur ces pages
– Index
– a. Algorithm: finite sequence of
well-defined instructions.
Algorithme déterministe: ce sont les plus
nombreux. Ils sont répétitifs. Ils reproduisent toujours le même résultat avec
la même séquence de calculs.
– syn. d'automate fini.
– a. Deterministic algorithm
Algorithme non déterministe: à chaque étape de
calcul plusieurs transitions sont possibles, le calcul développe un arbre et le
calcul est terminé que si le bout de toutes ces branches a été atteint. Un tel
algorithme est en général du type exponentiel.
– v. Machine de Turing
Algorithme d'Euclide: méthode pour
calculer le PGCD de deux
nombres.
– v. Algorithme d'Euclide
– a. Euclidean algorithm: efficient method for computing the greatest
common divisor (GCD) of two integers,
Algorithme de dieu: algorithme théorique le plus
court pour terminer le Rubik's
cube. S'applique aussi à d'autres casse-tête combinatoires.
– a. God's algorithm
Algorithme génétique: en l'absence de solution exacte
en temps raisonnable, procède par sélection naturelle appliquée à une
population de solutions.
– a. Genetic algorithm
Algorithme probabiliste: algorithme qui fait appel à des
donnés tirées au hasard.
– a. Randomized algorithm
Alignés:
veut dire situé sur une même droite; par deux points passe
toujours une droite; il faut donc un minimum de trois points pour parler
d'alignement.
– v. Colinéaire et coplanaire, diamétralement opposés.
– a. Three-point alignment,
colinear points.
Collinear points are
points that lie on the straight line.
Aliquote*: synonyme de diviseur.
– étym. Du latin aliquantum: assez
grande quantité.
Partie aliquote: qui est contenue un
nombre exact de fois dans un tout. Le nombre 5 est une partie aliquote de
10. Les parties aliquotes d'un nombre N
sont tous les diviseurs
de N sauf 1 et N. Aujourd'hui, on dit: diviseurs stricts ou diviseurs propres.
– v. Nombres parfaits
– a. Aliquot part,
aliquot sum, aliquot sequence.
Somme aliquote: somme des diviseurs
stricts.
– ex. pour 15, Sa = 1 + 3
+ 5 = 9.
Suite aliquote: un nombre est égal
à la somme des diviseurs du précédent
>>>
– v. Commensurable
Aliquante: qui n'est pas
aliquote, qui n'est pas diviseur d'un nombre. Le nombre 7 est une partie
aliquante de 10, car 7 ne divise par 10.

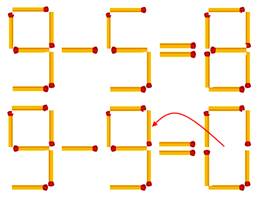
Allumette: tige de longueur
constante prétexte à des constructions géométriques et à des jeux.
– ex. Illustration: rétablir l'égalité en déplaçant une seule allumette.
– v. Jeux avec allumettes
– a. Matchstick games
Altitude: veut dire hauteur
en anglais.
– v. Hauteur
– a. Altitude: The distance measured perpendicularly from a figure's
vertex to the opposite side of the vertex.
Alternative:
une
proposition alternative énonce deux
choses dont une seule est vraie.
– ex. Il faut entrer ou
sortir
– v. Vocabulaire
de la logique
– a. Alternative proposal
Alterné (groupe -)**: groupe des
permutations paires d'un ensemble fini.
– a. Alternating group
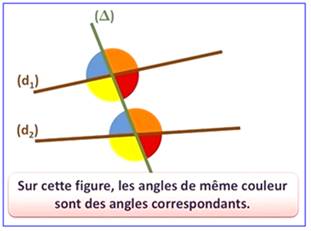
Alternes-internes et
alternes-externes: cas de deux parallèles et une
sécante:
les deux angles
de part et d'autre de la sécante respectivement internes aux parallèles, et
externes aux parallèles
– v. Types d'angles, correspondants
– a. Alternate interior angles,
alternate exterior angles, consécutive interior angles
Alphamétique: en récréation
mathématique, cryptarithme dans lequel les éléments forment des mots qui ont
une signification.
– ex. CINQ × SIX = TRENTE
=> 5409 × 142 = 768 078.
– v. Alphamétique
Amas: un amas désigne
une simple collection d’objets, sans structure particulière. C’est un synonyme
informel d’ensemble, utilisé parfois dans le contexte des structures
algébriques.
Ces objets peuvent être des nombres (comme 1, 2, 3), des lettres (a, b, c), ou
des entités plus abstraites comme des fonctions, des matrices, voire des
polynômes. À ce stade, il n’y a aucune règle imposée : c’est un village sans
lois.
Dès qu’on introduit une loi de composition interne (une règle pour combiner
deux objets de l’amas), on obtient ce qu’on appelle un magma.
Si cette loi respecte certaines propriétés (comme l’associativité, l’existence
d’un élément neutre, etc.), on peut alors définir des structures plus élaborées
comme des groupes, anneaux ou corps.
– v. Vocabulaire
des structures algébriques
– a. a cluster refers to a
simple collection of objects, without any imposed structure. It’s an informal
synonym for a set, sometimes used in the context of algebraic structures.
Ambiguïté** (théorie de
-) Théorie
exprimée par Galois
lors de sa recherche des racines
des équations. Galois cherchait des échanges à faire sans modifier les propriétés;
or il aboutissait à des impossibilités. Des "ambiguïtés" survenaient
comme solutions à des problèmes pourtant bien posés. D'abord vécues comme des
inconvénients, elles vont révéler une structure sous-jacente très riche.
Amiables ou amicaux (nombres
-): la somme des diviseurs
de l'un est égal à l'autre.
– ex. 220 et 284 sont deux nombres amiables.
– v. Nombres amiables
– a. Amicable numbers: two different natural numbers related in such a
way that the sum of the proper divisors of each is equal to the other number.
Amortissement*
pour
un emprunt bancaire, modalités de remboursement du capital
sans tenir compte des intérêts.
Le capital à amortir s'amenuise au fur et à mesure du paiement des mensualités
de remboursement
Intérêt composés
– a. Amortization refers to spreading payments over multiple periods.
Amortissement mécanique* diminution
progressive de l'amplitude d'un mouvement – v. Oscillatoire, pendule
– a. Damping
Ampère (A): Unité de base du système SI.
C’est l’intensité d’un courant électrique constant qui, maintenu dans deux
conducteurs parallèles, rectilignes, de longueur infinie et de section
circulaire négligeable, et placés à une distance de un mètre l’un de l’autre
dans le vide, produit entre ces deux conducteurs une force de 2 10-7
newton par mètre de longueur
– v. Unités, unités en électricité,
loi d'Ohm
– a. Ampere: the base unit of
electric current in the International System of Units (SI).
Amplitude: différence entre la
plus grande et la plus petite valeur d'une grandeur.
– ex: l'amplitude du mouvement du balancier d'une horloge; amplitude d'une sinusoïde
– v. Étendue, intervalle, encadrement
– v. Amplitude, peak-to-peak amplitude, root mean square amplitude
Anallagmatique**: se
dit d'une figure géométrique (comme une courbe, une spirale) globalement
invariante par inversion.
– étym. du grec allagma, changement
– a. anallagmatic:
curves that inverts into themselves are called anallagmatic curves.
Analogie: terme générique
pour ressemblance par identité, proportion … Du grec analogos, qui est en
rapport avec. Au sens strict, c'est l'égalité du rapport qui unit deux à
deux les termes de plusieurs couples. Ex : A / C = B / D. Autrefois désignait
la proportion.
Raisonnement par analogie: raisonnement, démonstration, qui tire des
conclusions en s'appuyant sur des ressemblances entre objets
Analyse: études des
fonctions et plus particulièrement liées aux notions de continuité et de limite.
Utilisation du calcul
algébrique, du calcul
différentiel ou du calcul
intégral.
– v. Analyse,
calcul infinitésimal
– a. Mathematical
analysis, calculus, differential calculus, calculus of variation
– note: le calcul
classique se dit computation
Analyse fonctionnelle**: branche des
mathématiques qui étudie les espaces de fonctions, et ce en dimension infinie.
Racines historiques: étude des transformations telles que la transformation de
Fourier et étude des équations
différentielles. Première brique: espaces de Banach.
Outil le plus simple: espaces de Hilbert (notion
d'orthogonalité).
Avancée principale: la théorie des distributions de Laurent Schwartz.
– a. Functional analysis, formulaic analysis
Sometimes functions can have dozens of
variables raised to high powers, defying formulaic analysis.
Analysis situ: ancien nom de la topologie.
Analytique: qui procède par
analyse, par résolution d'un tout en ses parties.
Analytique (maths): emploi pour la démonstration d’un théorème, ou la
solution d’un problème, du calcul algébrique, du calcul différentiel ou du
calcul intégral.
Fonction analytique*: fonction d'une
variable réelle ou complexe qui est développable en série entière au voisinage
de chacun des points de son domaine de définition.
– v. Holomorphe
– a. Analytic
function
Géométrie analytique: géométrie avec des nombres,
des coordonnées, des équations ou des inéquations.
– a. Analytic
geometry, cartesian geometrie: study of geometry using a coordinate system.
Méthode analytique: méthode de résolution des problèmes par l'analyse,
la recherche de loi générale, d'équations. Par opposition à la méthode empirique ou méthode expérimentale.

Anamorphose: déformation d'une
image par système optique
ou par transformations mathématiques.
– ex. Illustration: Anamorphose par Esher
– v. Transformation du boulanger
– a. Anamorphosis
Angle: figure plane formée
de deux demi-droites ayant même origine, le sommet de l'angle; les deux
demi-droites forment les côtés de l'angle; les angles se mesurent en degrés ou en radians (et grades,
parfois); symboles fréquents ![]() ; notation
; notation ![]() .
.
– v. Angle, types d'angles, polaire,
– types: Aigu, obtus, plat, saillant,
rentrant, extérieur, tangentiel, angle à la base
Opposés par le sommet,
alternes-internes, alternes-externes, correspondants,
adjacents, complémentaires,
supplémentaires
Azimut,
gisement, site, élévation, dépression
Gisement et cap, Tangage et roulis
– v. Angle, acute,
right, obtuse, straight, reflex, complete.

Angle géométrique (ou secteur angulaire) : deux demi-droites Ox, Oy de même origine O,
déterminent dans le plan deux régions, dont une seule est convexe (c’est-à-dire
que, si M et N sont deux points quelconques de cette région, le segment MN est
tout entier contenu dans cette région); cette région est appelée angle saillant
xOy. L’autre région est appelée angle rentrant. le point O est le sommet de
l’angle ; les demi-droites Ox, Oy en sont les côtés.
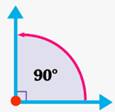
À chaque angle on peut associer un nombre
réel, positif ou nul, appelé sa mesure. Il y a trois unités de mesure d’angles
: le degré (°), le grade (gr) ou le radian (rd).
Angle de rotation: angle positif dans
le sens trigonométrique (contraire des aiguilles d'une montre) et négatif
sinon.
– v. Angle de
rotation
– a. Angle of
rotation, angular distance
Angle au centre: angle dont le sommet est au centre d'un cercle.
Les deux côtés sont des rayons.
Notion aussi applicable à un polygone.
– v. Angles dans le cercle
et théorème de l'angle inscrit et de l'angle au centre.
– a. Central angle:
the inscribed angle theorem states that an angle θ inscribed in a circle
is half of the central angle 2θ that subtends the same arc on the circle.
Angle inscrit: angle dont le sommet est sur un cercle; tous les
angles inscrits interceptant le même arc sont égaux (ont la même mesure).
L'angle inscrit vaut la moitié de l'angle au centre interceptant le même arc.
– ex. Un angle
inscrit dans un demi-cercle est droit
– v. Angles dans le cercle
 – a. Inscribed
angle.
– a. Inscribed
angle.
Angle droit: angle dont l'ouverture est de 90°.
– symb. ∟
– v. Angle droit
– a. Angle
Angle orienté: angle dont les côté sont des vecteurs et munis d'un sens positif (sens
inverse des aiguilles de la montre) ou négatif. Sans orientation, l'angle est
géométrique.
![]()
![]()
Angström: unité de mesure de
longueur tolérée avec le système SI
équivalent à 10-10 mètre, soit 1/10 de nanomètre
ou 100 picomètre
– symb. ![]() (unicode 00C5)
(unicode 00C5)
– ex. Rayon atomique
entre 0,25 et 3 Å
– v. Angström, puissances de 10
– a. Angstrom: one
ten-billionth (US)
Anneau*:
ensemble
doté de deux lois de
composition interne, la première lui donnant une structure de groupe commutatif,
la seconde étant associative et distributive par rapport à la première.
– ex. L'ensemble des nombres entiers rationnels ![]() forment un anneau avec l'addition et la multiplication.
forment un anneau avec l'addition et la multiplication.
– v. Anneau, groupe, corps,
structure
algébrique
– a.
Ring
Anneau unitaire: autre nom de l'anneau.
Anneau quotient: ![]()
– v. Lettre
Z et sa signification en maths
Annulation: simplification,
réduction d'une expression.
– a. Cancellation
Antécédent:
dans
une application, l'élément a
donnant b pour image est
l'antécédent de b.
– v. vocabulaire
des structures algébriques
Antécédent (s) d'un nombre y par une fonction: abscisse(s) de tous
les points de la courbe représentative ayant une ordonnées égale à y.
Ou aussi, valeurs de x en résolvant f(x) = y.
Avec x donné, la valeur de y est l'image; avec y donné, la valeur de x est
l'antécédent.
– ex. Antécédent de –1
par la fonction f(x) = 2x – 5. On résout 2x – 5 = –1 qui donne x = 2. Le nombre
–1 a une antécédent: 2.
Antécédent: en logique,
la première proposition, prémisse
d'un raisonnement.
– ex. Dans "si A,
alors B" , A est l'antécédent et B est le conséquent.
– a. Antecedent and
consequent
Anticentre du
quarilatère: les medhauteus sont les segment issu du milieu d'un côté et perpendiculaire
au côté opposé.
Dans un quadrilatère cyclique, les quatre
medhauteurs sont concourantes en un point nommé anticentre. Le centre de
gravité est au milieu du segment joignant l'anticentre et le centre du cercle
circonscrit.
Antidéplacement: déplacement,
mais avec un angle opposé (un retournement de la figure).
Les réflexions ou les composées d'une réflexion et d'une translation sont des
antidéplacements.
– v. Déplacement, transformations
Antihoraire (sens -): sens opposé à celui
de la rotation des aiguilles d'une horloge. Synonyme de sesn trigonométrique.
– v. Horaire, angle de
rotation
Antiparallèle: relatif à deux
couples de droites dont les bissectrices des angles sont parallèles.
– v. Ligne isogonale
– a. Antiparallel lines
Antipodal (point -): point
diamétralement opposé à un point donné.
Deux points antipodaux sont situés aux extrémités d'un diamètre.
– a.
Antpodal or diametrically opposite points: they are the endpoints of a
diameter.
Antiprisme: en gros, prisme déformé par rotation de
l'une de ses faces.
– v. Antiprisme
– a. Antiprism
Antisymétrique
(application - ): si f(x) = - f(x)
– v. Application, symétrique,
vocabulaire
des structures algébriques
– a. Antisymmetric
relation
Antisymétrique (relation -)**: telle que: ![]()
– ex. x ³ y et y ³ x alors x = y
– v. Symétrique, transitive, relation d'ordre,
inégalité
– a. Antisymmetric
relation
Apagogie: désigne le raisonnement par l'absurde.
– v. Raisonnement
par l'absurde
– a. Reductio ad absurdum:
Apex: sommet de certains solides.
– ex. L'apex du cône, de la pyramide, du prisme; la face
opposée à l'apex est la base du solide
– a. En anglais apex
veut dire sommet, pluriel apexes ou apices
Apollonien (remplissage
-): avec des disques, les plus gros sont en contact. Les vides sont remplis
avec des disques plus petits, mais les plus grands possible (Illustration).
– v. Fractales, baderne d'Apollonius
– v. Apollonian gasket
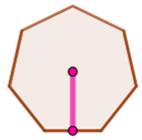 Apothème (un): en 2D,
segment perpendiculaire à un côté d'un polygone régulier
et passant par son centre; distance du centre d'un polygone régulier à l'un de
ses côtés. Rayon du cercle inscrit au polygone.
Apothème (un): en 2D,
segment perpendiculaire à un côté d'un polygone régulier
et passant par son centre; distance du centre d'un polygone régulier à l'un de
ses côtés. Rayon du cercle inscrit au polygone.
– ex: la surface d'un polygone régulier est égale au
produit de son demi-périmètre par la longueur de son apothème.
– v. Segment, apothème du pentagone, apothème du décagone
– a. Apothem: in a regular
polygon, a line segment from the center to the midpoint of one of its sides.
Lorsque le nombre de côtés du polygone tend
vers l'infini, l'apothème
s'apparente au rayon du cercle
limite. Voir Sagitta dans un cercle
(Apothème + sagitta = rayon du cercle).
Apothème: en 3D, pour des solides réguliers.
- dans un polyèdre,
c'est la distance d'un sommet à un côté. Hauteur dessinée sur une face;
- dans le prisme
ou la pyramide, c'est
la hauteur d'une face latérale; segment issu du sommet et perpendiculaire à un
côté de la base;
- dans le cône,
c'est une oblique issue du sommet et joignant un point du cercle de base.
Apparente
(singularité -)**: un point où la fonction n'est pas définie, mais où il est possible d'y
redéfinir la fonction de manière à rendre créer un voisinage régulier
– a. Removable singularity
Appartenance: l'élément a appartient à l'ensemble
E;
![]() signifie que l'élément a n'appartient
pas à l'ensemble E;
signifie que l'élément a n'appartient
pas à l'ensemble E;
![]() signifie que l'ensemble E contient l'élément
a;
signifie que l'ensemble E contient l'élément
a;
![]() signifie que ces cinq nombres font partie de
l'ensemble E.
signifie que ces cinq nombres font partie de
l'ensemble E.
– v. Symboles, négation, inclusion
– a. "is an element of" or
set membership or x is a member of E or x belongs to E.
Appartient: un élément ou un
sous-ensemble qui est contenu dans un ensemble (symbole Î)
– v. Élément, ensemble
– a. Belong to
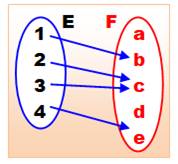 Application: généralisation du
concept de fonction.
Application: généralisation du
concept de fonction.
Relation entre deux ensembles
E (départ ou source) et F (arrivée ou but) telle qu'à chaque élément de E
corresponde un élément de F unique, appelé image.
Si la relation est de E dans E (donc sur lui-même), l'application est appelée transformation
– ex. Application qui, à chaque carte
d'un jeu, associe sa couleur.
– v. Application et bijection, loi, bijection, injection,
surjection, morphisme,
vocabulaire
des structures algébriques
– v. Différence entre application et
fonction
– a. Map, mapping: often refers to the
action of applying a function to the elements of its domain
– note: application: map et carte:
chart.
Application linéaire
(transformation linéaire): idée de deux fonctions (applications) pondérées
chacune par un coefficient et sommée: ![]() .
.
Évidemment généralisable à plus de deux fonctions
– v. Linéaire

Application (informatique): programme utilisé pour réaliser une tâche ou un
ensemble de tâches. – syn. Logiciel.
– ex. Éditeur de texte (Word ou autre), jeu vidéo, navigateur web
– a. Application program, computer program for the end-users. A computer
program designed to help people perform an activity
Appliquer: appliquer un
théorème, une règle, une procédure, un algorithme.
Utiliser une loi connue pour
conduire un raisonnement,
une démonstration.
– v. Techniques de base de l'algèbre, mots usuels du calcul
– a. Apply: it is important to know when to
apply the Pythagorean theorem0
Apprentissage
automatique: traduction de l'anglais: machine learning
– a. Machine
learning
Approché (calcul -): méthode de calcul
permettant de trouver des solutions proches de la solution réelle.
– a. Approximation calculus
Approximation: valeur voisine d'un
nombre; par défaut ou par excès
– syn.
Valeur approchée
– notation: ![]()
– v. Arrondi, troncation, incertitude et précision
– a. Approximation: not exact, but close
enough to be used. An approximation can be obtained by rounding, estimating or
truncating.
Approximation décimale d'une
fraction: valeur décimale de la fraction irrationnelle;
– ex: 2/7 = 0,285…
– v. Réduites
– a. Convergents
Approximations
successives (par-): évaluer une valeur par des estimations de plus en
plus proche de cette valeur.
– a. By successive approximations
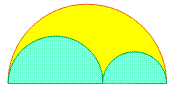 Arbelos: figure géométrique (partie jaune) égale à l'espace compris
entre deux demi-cercles inclus dans un grand demi-cercle.
Arbelos: figure géométrique (partie jaune) égale à l'espace compris
entre deux demi-cercles inclus dans un grand demi-cercle.
– v. Arbelos,
cercle et son
vocabulaire / Énigme des
cinq cercles
– a. Arbelos
Arbre des facteurs: décompositions
successives d'un nombre en facteurs pour
aboutir aux facteurs premiers;
– ex. 100 = 4 x 25 puis 4 = 2 x 2 et 25 = 5 x 5
(Illustration)
Arbre: graphe
classique se déployant en branches, et tel que toutes les branches sont
connectées et il n'y a pas de boucles.
En bref: graphe non orienté connexe et sans cycle.
Utilisation typique en dénombrement
– a. Tree, connected graph
without a cycle.
Arbre des possibilités ou des
probabilités ou graphe des probabilités:
dessin représentant des chemins de cas possibles, chaque branche étant affectée
d'une probabilité.
Schéma utilisé pour dresser la
liste des parties d’un ensemble, faire un dénombrement (en calcul de
probabilités, par exemple).
Technique de calcul qui est aux probabilités ce qu'est la division posée pour
le calcul des quotients.
– v. Arbres pondérés
avec l'exemple des écoliers
– a. Tree diagram in probability
theory
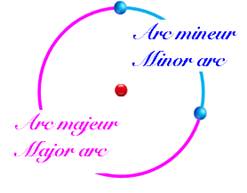 Arc de cercle: portion d'un cercle,
d'une courbe, limitée par deux de ses points; deux points sur un cercle
délimitent deux arc de cercles
Arc de cercle: portion d'un cercle,
d'une courbe, limitée par deux de ses points; deux points sur un cercle
délimitent deux arc de cercles
Généralisation à tout arc de courbe
– v. Secteur, sous-tendre, capable, ellipse, demi-cercle
– v. Cercle, cercle et son vocabulaire,
arcs, cordes et
sagittas
– a. Circular arc: a part of the
circumference is called an arc
Arc de grand cercle: sur une sphère, portion d'un grand cercle (le plan d'un tel cercle passe
par le centre de la sphère); c'est une géodésique sur la sphère.
Arc majeur de grand cercle: le plus grans des deux arcs sur un même grand cercle.
Arc mineur de grand cercle: le plus petit des deux arcs sur un même grand cercle.
– a. major arc and minor arc
Arc tangente: l'arc tangente d'un nombre
x est un nombre réel
dont la tangente est x; même chose pour arc sinus, arc cosinus, arc cotangente, arc sécante et arc cosécante; d'une manière générale, retrouver
l'angle lorsqu'on connaît sa
fonction trigonométrique.
–
notation. y = arctan(x) ⬄ x = tan(y)
– v. Arc tangente, trigonométrie
– a. Arctangent, arctan
Arc
d'un graphe: arête dans un graphe orienté.
– a. Edge: undirected edges are called lines and directed edges are
called arcs or arrows.
Archimède (loi ou
principe d'-): Tout corps plongé dans un liquide est soumis à une poussée verticale
ascendante égale au poids
du volume de liquide déplacé.
– v. Eurêka d'Archimède
– a. Archimedes' principle
Archimédien: se dit d'un
ensemble qui est ordonné.
Pour deux grandeurs inégales, il existe toujours un multiple entier de la plus
petite, supérieur à la plus grande.
Plus précisément: pour tous les éléments a et b tels que ![]() , il existe un
entier naturel tel que
, il existe un
entier naturel tel que ![]() .
.
Cette notion implique qu'un ensemble ayant cette propriété n'est pas limité.
– ex. le corps des rationnels
et celui des réels
![]() sont archimédiens. Les complexes comme les p-adiques ne le sont pas.
sont archimédiens. Les complexes comme les p-adiques ne le sont pas.
– v. relation
d'ordre
– a. archimedean property

Arcsin, arccos, arctan:
fonctions
réciproques des sinus, cosinus, tangente, cotangente, sécante et cosécante,
dites fonctions circulaires réciproques. Elles
retournent la valeur de l'angle qui correspond à la valeur du sinus, du cosinus
ou de la tangente. Ex: arsin(1/2) = 30°. Propriété: arcsin(x) + arccos(x) =
90°.
– v. Lignes
trigonométriques réciproques, exemple
de calcul
– a. arcsine, arccosine, arctangent, arccotangent
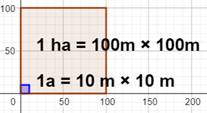 Are: vaut 100 m²; un carré de 10m de côté; ex: un terrain
à bâtir de 500 m² correspond à 5 ares
Are: vaut 100 m²; un carré de 10m de côté; ex: un terrain
à bâtir de 500 m² correspond à 5 ares
Hectare: vaut 100 ares
soit 10 000 m²; un carré de 100 m de côté; soit, environ un terrain de
football; une ferme de 100 ha dispose de l'équivalent de 1 km².
– v. Tableau de
correspondance, hectare
Arête: la limite entre les
faces d'un cube ou
de tout autre solide comme les polyèdres;
segment reliant deux sommets consécutifs d'une même
face d'un solide géométrique; ex: les douze arêtes du cube ou de n'importe quel parallélépipède.
Droite commune à deux plans sécants.
– a. Edge: arête / Vertices: sommet / Face: face
Arête ou branche d'un graphe: chaque ligne qui
joint deux sommets dans un graphe.
– v. Vocabulaire des
graphes
– a. Graphe:
a structure made of vertices and edges
Arête d'une ligne polygonale: chaque segment de
cette ligneP.htm#POLY polygonale.
– a. Polygonal chain: a connected series of line segments.
Argument d'une
fonction: synonyme de variable, notamment en parlant des
fonctions trigonométriques;
ex: dans f(x) = sin (x), x est l'argument
de la fonction sinus x
Argument d'un nombre complexe* angle ![]() caractérisant un nombre complexe.
caractérisant un nombre complexe.
– v. Vocabulaire des nombres
complexes, module
– a. Arguement or phase
Arité: nombres
d'arguments dans une fonction ou nombres d'opérandes dans une opération. Aussi,
la quantité de connecteurs dans une fonction booléenne.
– ex. L'addition de deux nombres est une fonction binaire; son arité est 2.
– type: monadique, binaire, ternaire, … k-aire.
– v. Opérateur, opération
– a. Arity: An operation of arity zero, or nullary operation, is a constant.
Ex: Unary operations (i.e. operations of arity 1), such as additive inverse and
multiplicative inverse.
Arithmétique: branche des mathématiques
qui traite des nombres entiers
ainsi que de la résolution de problèmes numériques par le biais d’opérations
simples.
Partie des mathématiques
qui s'intéresse aux nombres et aux opérations sur ces
nombres. Partie des
mathématiques qui étudie l’ensemble ℕ des nombres entiers naturels, c’est-à-dire positifs (0, 1, 2, 3, 4,
etc.), et ![]() , ensemble des entiers relatifs,
c’est-à-dire positifs et négatifs (... , - 4, -3, -2, - 1, 0, 1, 2, 3, 4, ..).et les opérations dans ces ensembles,
divisibilité, nombres premiers, etc.
, ensemble des entiers relatifs,
c’est-à-dire positifs et négatifs (... , - 4, -3, -2, - 1, 0, 1, 2, 3, 4, ..).et les opérations dans ces ensembles,
divisibilité, nombres premiers, etc.
– étym. mot qui vient du grec arithmos, nombre.
– v. Arithmétique,
calcul, théorie des nombres
– v. Portail arithmétique et
algèbre
Arithmétique (moyenne -): il existe divers
type de moyennes: arithmétique, géométrique, harmonique, héronienne,
quadratique, arithmético-géométrique.
– v. Moyennes
– a. Mean, arithmetic mean, geometric mean, harmonic
mean
Arithmétique (suite ou
progression): nombres dont chacun est égal au précédent plus une constante, appelée raison de la progression arithmétique.
– v. Suites
– a. Arithmetic
progression or arithmetic sequence: a sequence of numbers such that the
difference between the consecutive terms is constant.
Arithmétique (théorème fondamental
de l' -): tout nombre (supérieur à 1) est égal à un produit de nombres premiers et
cela de façon unique (à l'ordre près des facteurs).
– ex. 630 = 2 × 3² × 5 × 7
– v. Théorème
fondamental de l'arithmétique
– a. Fundamental theorem of arithmetic or unique
factorization theorem
Arithmétique (triangle -): tableau de nombres organisé en triangle, chacun reprenant un coefficient binomial,
autrement-dit la quantité de choix de k parmi n.
– v. Triangle de Pascal
– a. Pascal's triangle
Arithmétique modulaire: arithmétique qui ne
s'intéresse qu'aux restes des divisions.
Pensez à la manière dont vous compter les heures. Remise à zéro au passage par
12.
– vocab. Congruences, modulo,
résidus.
– v. Arithmétique
modulaire
Modular arithmetic
Unité arithmétique et logique (UAL ou
ALU): cœur de votre ordinateur, là où se déroulent toutes les opérations
(arithmétiques comme logiques), y compris la commande des échanges avec les
mémoires.
Ensemble de circuits électroniques connectés logiquement de façon à réaliser,
sous l'action de commandes élémentaires, les opérations arithmétiques ou
logiques pour lesquelles cet ensemble a été conçu.
– v. Unité arithmétique et
logique, ordinateur,
comment ça marche, microprocesseur
– a. Arithmetic and logic unit (ALU)
Arrangement: combinaison de p éléments parmi q mais l'ordre est important (Aqp)
Dans un ensemble E de p éléments, sous-ensemble ordonné de q
éléments de E pris sans répétition.
ex: pour E = {1, 2, 3}, les arrangements possibles de 2 parmi 3 sont: {1, 2},
{1, 3}, {2, 3}, {2, 1}, {3, 1}, {3, 2}, soit 6 arrangements.
– v. Arrangement, dénombrement
– a. Partial permutation or sequence without repetition
ARRANGEMENTS AVEC RÉPÉTITIONS
Cherchons à former, avec les lettres x et y,
tous les mots possibles de trois lettres, chaque lettre x ou y pouvant figurer
une ou plusieurs fois; on obtient huit mots : xxx, xxy, xyx, yxx, xyy, yxy,
yyx, yyy. On dit qu’il y a huit
arrangements, avec répétition, des deux lettres x et y, prises trois par trois.
Définition par une application: deux ensembles E {a, b} et F {x, y, z}. Quelles
sont toutes les applications de E dans F ? Il faut connaître l'image de a
et l'image de b. Pour chacun, il y a trois choix. Donc 3 x 3 = 9 applications
possibles.
Si E est un ensemble à p éléments et si F est
un ensemble à n éléments, il y a np applications de E dans F
(puisqu’on peut choisir l’image de chaque élément de E parmi les n éléments de
F).
Dans le cas où E est {1, 2, 3, … , p}, une
application de E dans F est appelée un arrangement avec répétition de n
éléments pris p à p (il y en a np).
Si E = {1, 2, 3} et F = {x, y}, les
applications de E dans F sont au nombre de 23 = 8.
ARRANGEMENTS SANS RÉPÉTITIONS
Deux ensembles : E = {a, b} et F = {x,
y, z}. On cherche le nombre d’applications
injectives de E dans F. L’image de a peut être x, y ou z, celle de b doit être distincte de celle de a
; donc, si celle de a est x, celle de b ne peut plus être que y ou z ; il y a
trois choix possibles de l’image de a, mais, après dans F chaque choix de
l’image de a, il n’y a plus que deux choix possibles de l’image de b. II y a
donc six choix possibles seulement pour le couple (image de a, image de b).
Si E = { 1, 2, . , p } : une telle
application est appelée arrangement sans répétition de n éléments pris p à p.
Le nombre de ces arrangements est noté Apn.
Ex. E = {1, 2, 3} et F = {a, b, c, d, e}. Le
nombre des arrangements des cinq éléments de F pris trois par trois est : A35
= 5 x 4 x 3 = 60. Ces arrangements sont : abc, abd, abe ...
Arrondir,
arrondissement: prendre un nombre voisin comportant moins de décimales, ou pas du tout
(12,6 devient 13; p = 3,1415926…
arrondi au centième devient 3,14)
Procédé: si le dernier chiffre à
arrondir est 0, 1, 2, 3 ou 4, il est annulé; sinon, il est annulé et
l'avant-dernier chiffre est augmenté de 1; ex: 1,24 est arrondi à 1,2; 1,25 est
arrondi à 1,3 et 1,26 est arrondi à 1,3.
Arrondir à l'unité: arrondir la partie entière du nombre décimal en
tenant compte des dixièmes. Ex: 123,456 est arrondi à l'unité par 123 et 123,5
est arrondi à l'unité par 124.
– v. Arrondir, tronquer …
– a. Round
Ascension droite: l'ascension Droite, ou AD est
équivalente à la longitude sur la sphère terrestre.
L'autre angle est la déclinaison.
– v. Sphère terrestre
– a. Right ascension (RA), declination
Assertion:
proche
de proposition.
Une assertion est un énoncé présenté comme vrai mais qui n'est pas encore
vérifié voire non vérifiable, et même potentiellement faux.
– v. Incomplètude,
théorème (une assertion démontrée)
– a. Assertion
Associativité: le regroupement des
termes, en conservant l'ordre, ne change pas le résultat de l'opération.
Indique le fait que l'ordre n'importe pas dans une suite d'additions ou de
multiplications.
- l'addition
est associative a + (b + c) = (a + b) + c = a + b + c
- la multiplication
est associative a (b . c) = (a . b) c = a . b . c
- la soustraction
et la division
ne sont pas associatives
– v. Commutativité, distributivité, vocabulaire des structures
algébriques
– a. Associative property, associativity: means that rearranging the
parentheses in an expression will not change the result. In propositional
logic,
ASSOCIATIF, Associativité: si l’ensemble E
est muni d’une loi de composition interne notée *, cette Ioi permet de composer
deux éléments de E ; pour composer trois éléments de E, on compose d’abord deux
d’entre eux, puis le résultat ainsi trouvé avec le troisième. Par exemple, pour
composer a, b et c (dans cet ordre), on a le choix entre composer d’abord b et
c et composer a avec le résultat ainsi trouvé, ce qui s’écrit a *(b * c), ou
composer a et b et le résultat ainsi trouvé avec c, ce qui s’écrit (a * b) * c.
La loi * est dite associative si, quels que soient les éléments a, b, c de E,
les deux éléments calculés ci-dessus sont égaux : a *(b * c) = (a * b) * c. Ces
composés sont notés a*b*c.
C'est le cas pour l'addition et la
multiplication dans ![]() ; mais pas pour la soustraction.
; mais pas pour la soustraction.
Astérisque (*): en indice d'un nom d'ensemble,
veut dire que le zéro est exclu de l'ensemble; ex ![]() .
.
– v. Cas de l'ensemble Z
– a. Asterisk
Asymptote: une droite est
asymptote à une courbe lorsque celle-ci s'en approche de plus en plus sans
l'atteindre vraiment; l'écart tend vers 0.
– v. Quantité de spires sur une
bobine, limite,
hyperbole
– a. Asymptote
Une courbe et une droite. Si l’on appelle M
le point de la courbe d’abscisse x et P le point de la droite de même abscisse
x, si la distance de M à P a pour limite 0 quand le point M s’éloigne
indéfiniment sur la courbe alors la droite est l'asymptote de la courbe.
Équation f(x) pour la courbe et ax + b pour la droite. La droite est asymptote
si la différence f(x) – (ax + b) a pour limite 0 quand x tend vers + ꝏ
ou – ꝏ .
Atan2(y,
x)*: angle entre l'axe des x et la droite OM, M étant le point de coordonnées
(x, y). Angle en radians entre l'axe des abscisses et la droite qui joint
l'origine O des axes et le point M (x, y). Angle positif dans le demi-plan
supérieur (sens trigonométrique ou antihoraire).
– origine: trouver une fonction
qui renvoie la valeur correcte et non ambigüe de l'angle lorsqu'on convertit
des coordonnées cartésiennes (x, y) en coordonnées polaire (![]() )
)
– v. relations
trigonométriques
– a. Atan2(x,y)
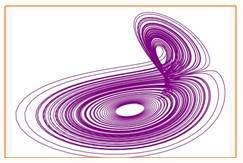
Attracteur: la théorie du chaos
affirme que, même si des événements sont divergents, au final et
statistiquement, ils s'accumulent sur un noyau de trajectoires nommé
attracteur.
– v. Attracteur
étrange
– a. Butterfly effect: sensitive dependence on initial conditions, chaos theory
Autant:
exprimé
une égalité.
– a. As much as, as many as (pour autant que: as long as)
Automate: un ordinateur est un exemple
d'automate; d'une manière générale, un automate est une machine qui sait créer
des sorties (des commandes) à partir de données d'entrée, tout en se souvenant
de son passé; l'automate entretient des variables d'état internes qui servent à
tenir compte du passé des opérations.
– v. Automate
– a. Automaton
Automorphisme* isomorphisme
d'un ensemble sur lui-même.
– ex. la fonction sin(x) est
automorphique: on la retrouve pour x + 2kπ.
– v. Morphisme,
Langlands Program (recherche généralisée
d'automorphismes)
– a. Automorphism
Autosimilarité ou
invariance d'échelle: cas d'une figure qui se reproduit de manière semblable à différentes échelles.
Même forme et même structure quels que soit les zooms sur la figure.
Propriété qui reste vraie à toutes les échelles.
Si on regarde une portion de fractale, il est impossible de spécifier l'échelle
à laquelle nous l'observons.
– ex. la boîte de
vache qui rit en guise de boucle d'oreille de la vache représentée sur la boîte
de vache qui rit .
– v. Fractale
– a. Self-similarity: a self-similar object is
exactly or approximately similar to a part of itself.
Scale invariance
Avant-dernier ou
pénultième
–
a. last but one, penultimate
Axe: dans un repère,
demi-droite graduée; elle a une origine, un sens, et une graduation; droite
orientée munie d'une origine et d'une unité.
Axes (système d'-): synonyme de base ou repère, mot préféré ou encore de
système de coordonnées
– v. Base, repère et référentiel
– a. Coordinate system.
Axes de référence: axes définis par un
repère cartésien;
synonyme de base de référence.
Axe des abscisses et axe des
ordonnées: respectivement, axes des x (horizontal) et axe des y (vertical) dans un
repère du plan.
Tous eux des axes de nombres.
– v. Abscissa and ordinate. The X axis runs horizontally through zero; the Y axis runs vertically
through zero. One axis and
several axes.
Axe des nombres: Droite ou demi-droite orientée (flèche) et graduée avec des nombres.
– attention: ne pas confondre
avec la droite numérique qui représente tous les nombres, alors que l'axe est gradué avec les
seuls nombres choisis.
Axe de rotation: droite de l'espace (ordinaire ou affine) dont les
points restent invariants dans une rotation.
Droite
fixe (réelle ou imaginaire) autour de laquelle s'effectue la rotation.
– ex. L'axe d'un cylindre, l'axe d'un disque.
– note: notion plutôt
utilisée en physique pour caractériser un mouvement, une action dynamique. Par
exemple, l'axe de rotation de la Terre (sur elle-même).
– v. Rotation
– a. Rotation axis, rotation around a fixed axis
Axe de révolution: droite autour de
laquelle tourne une figure géométrique qui engendre un solide.
Droite fixe autour de laquelle tourne une courbe donnée (courbe génératrice)
engendrant une surface de révolution.
– v. Axe
de révolution et génératrice avec exemples
– a. Axis of revolution,
– note: en physique, par
exemple, l'axe de révolution de la Terre autour du Soleil.
– a. Earth orbit: Earth appears to revolve in a counterclockwise direction around the
Sun.
Axe de symétrie: droite partageant la
figure en deux parties-miroir.
Droite par rapport à laquelle la figure est invariante
par symétrie axiale.
– v. Symétrie, symétrie axiale
– a. Symmetry axis
Axe de symétrie d'une figure: axe d'une symétrie
dans laquelle la figure est globalement invariante.
– a. axial symmetry
Axe radical d'un faisceau de cercles: droites passant
par les deux points d'intersection ou droite de tangence commune.
– v. Faisceau
de cercles
– a. Radical axis
Axiome: vérité évidente;
hypothèse initiale dans une théorie mathématique; proposition élémentaire
admise comme vérité; énoncé d'une propriété vraie a priori; qu'il faut admettre
comme point de départ d'une théorie; synonyme de postulat;
– ex: deux quantités égales à une troisième
sont égales entre elles; le tout est plus grand ou égal à l'une de ses parties
…
– étym. vient du grec axioma, j'estime, je tiens pour vrai;
dérivé de axioô, juger convenable, croire juste
– v. Démonstration, théorème, axiome, hypothèses, etc.
– a. Axiom, postulate, assumption: statement that is taken to be true, to serve
as a premise or starting point for further reasoning and arguments.
Au départ d’une théorie mathématique, il y a
:
![]() d’une
part, des termes primitifs que l’on ne définit pas ; par exemple, pour la
géométrie : point, droite, plan, etc. ; pour les ensembles : ensembles,
éléments, - - etc. ;
d’une
part, des termes primitifs que l’on ne définit pas ; par exemple, pour la
géométrie : point, droite, plan, etc. ; pour les ensembles : ensembles,
éléments, - - etc. ;
![]() d’autre
part, des axiomes ou propositions vraies par définition.
d’autre
part, des axiomes ou propositions vraies par définition.
Ces axiomes ne sont pas toujours des
propriétés évidentes mais sont des énoncés posés a priori, qui doivent
constituer un système cohérent (non contradictoire) à partir duquel sera
édifiée la théorie.
Axiomes de Peano: la définition de
l’ensemble des entiers
naturels ![]() repose
repose
- sur les termes primitifs : 0, entier naturel, successeur ; et
- sur les axiomes suivants:
1) 0 est un entier naturel ;
2) tout entier naturel a un successeur
;
3) deux entiers naturels ayant même
successeur sont égaux ;
4) 0 n’est le successeur d’aucun
entier naturel ;
5) si une partie P de N, contenant 0,
est telle que le successeur de tout élément de P appartienne à P, alors cette
partie P de N est égale à N.
– a. Peano axioms or
Dedekind–Peano axioms or the Peano postulates
Azimut: classiquement: direction
"horizontale" par rapport
au nord;
– ex: Une église située en plein Est se trouve
à 90° d'azimut.
Un amer (point remarquable sur la côte) est à 40° d'azimut alors que mon navire
progresse dans l'azimut 20°, cet amer se trouve, ainsi, dans un gisement de 20° par rapport à ma direction (ma route sans
dérive).
– étym. de l'arabe as-simt, direction
– v. Emploi du GPS
– a. Azimuth.
– note: en anglais azimuth prend un h à la fin (th est usuel en anglais, pas en
français).
Azimut:
en coordonnées polaires,
synonyme d'angle polaire,
noté ![]() .
.
– v. Gisement et cap,
tangage et roulis
Azimut d'un point géographique: angle horizontal,
compté dans le sens des aiguilles d'une montre à partir du sud en astronomie et
à partir du nord en géodésie.
– v. Gyroscope
![]()
|
Voir |
|
|
Aussi |
|
|
Autres |
|
|
Cette page |
![]()