|
Édition du: 03/07/2025 |
|
INDEX |
TOPOLOGIE |
||
|
Outils de la topologie |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
VARIÉTÉ TOPOLOGIQUE
Une variété topologique est un
espace qui, localement, ressemble à un espace classique (espace euclidien). Autrement dit,
autour de chaque point, la variété "ressemble" à un morceau du
tout. La
variété ressemble localement à une droite,
un plan,
ou autre, mais le tout peut avoir une structure globale
différente et plus complexe. En simplifiant
: partout où l’on zoome sur la variété, on retrouve une portion de ligne ou
de surface familière. |
||
|
|
Sommaire de cette page >>> Variété en topologie >>> Propriétés des variétés >>> Particularités et Actualités >>> Exemples de variétés >>> Étymologie (Mannigfaltigkeit) >>> Comparaison >>> Variétés et bords >>> Historique |
Débutants Glossaire |
Anglais: Topological manifold
or topological space
|
Présentation Les variétés
topologiques sont des objets mathématiques qui permettent de généraliser
notre compréhension des formes et des espaces. Parfois, pour simplifier, on dit
que la notion de variété est une généralisation
de la notion de surface à toutes les dimensions. Les variétés
apparaissent dans plusieurs domaines des sciences, comme la physique,
l’informatique et l’ingénierie. L’idée générale
est que les objets étudiés, même s’ils peuvent être courbés ou enroulés,
ressemblent toujours, à petite échelle, à des espaces plus simples comme la
droite ou le plan. C’est cette propriété qui définit une variété topologique. Analogie Intuitivement,
une variété topologique de dimension 2 est un espace qui, localement, c’est à
dire si on ne regarde pas trop loin, ressemble à un petit morceau de feuille
de papier qu’on aurait pu découper avec des ciseaux après en avoir tracé le
pourtour au crayon (on peut d’ailleurs froisser le bout de papier en
question). La structure
globale de cet espace peut être évidemment assez différente puisque la
variété elle-même est obtenue par recollement de tous ces petits morceaux de
papier. Ainsi, un pneu
de bicyclette, éventuellement dégonflé, plié et froissé fournit un exemple
d’objet physique qu’on peut modéliser à l’aide d’une variété topologique de
dimension 2 : un tore. Définition Une variété
topologique est un espace qui ressemble localement à un espace euclidien (une
droite, un plan, etc.), mais qui peut avoir une structure globale différente
et bien plus complexe. En termes plus
simples : partout où l’on zoome sur la variété, on retrouve une portion de
ligne ou de surface familière. Une variété
topologique est tout d’abord un espace topologique, mais on suppose, de
surcroît, que chacun de ses points possède un voisinage homéomorphe (semblable par
simple déformation).
Mathématique Une variété algébrique est l'ensemble des
solutions d'une ou plusieurs équations polynomiales. Il existe trois grandes
classes de géométries: hyperbolique, plate et sphérique. À chacune correspond une classe de variétés,
respectivement: général, de Calibi-Yau et de Fano. Ces variétés sont si foisonnantes que les
mathématiciens cherchent à utiliser l'IA pour les classer. |
|
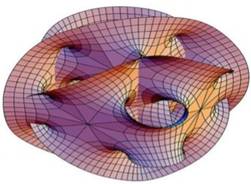
Variété
de Calibi-Yau et Variété de Fano de dimension 3

Source images: La
Recherche N° 579 – oct-nov-déc 2024
L'IA aide à classer les formes géométriques
abstraites – Charlotte Mauger
|
Dimension La dimension
d’une variété correspond au nombre minimal de coordonnées
nécessaires pour décrire un point dans un voisinage un point. |
|
|
|
Propriétés topologiques Caractéristiques de forme: un seul bloc (continu)
ou pas; présence de trous ou pas; … |
Une variété est connexe si elle est formée d’un seul morceau. Par exemple, une
sphère est connexe,
tandis que deux cercles séparés ne le sont pas. La simple
connexité signifie que toute boucle peut être réduite à un point sans
découper la variété. Une sphère
est simplement connexe, tandis qu’un tore ne l’est pas Une
variété est compacte si elle est bornée et fermée, comme une sphère. Elle est
non compacte si elle s’étend à l’infini, comme un plan ou une droite. Certaines variétés possèdent une limite. Par
exemple, un disque
(cercle rempli) possède un bord, alors que la sphère en est dépourvue. |
|
|
Applications Les variétés sont utilisées dans plusieurs
domaines. |
|
|
|
Un concept de base en topologie est la
"variété", une forme qui est la même partout, c'est-à-dire qu'elle
n'a pas de points d'extrémité, de points d'arête, de points de croisement ou
de points de ramification. |
A basic concept in
topology is the “manifold”, a shape that is the same everywhere, meaning that
it has no end points, edge points, crossing points or branching points. |
Actualités
|
La notion de variété introduit un espace
topologique localement euclidien mais qui peut être globalement plus complexe
à l’image de la sphère, où, par exemple à la surface de la Terre, on a
l’impression que la surface est localement plate sans que cela soit vrai
globalement. |
Un sujet crucial consiste en la classification
des variétés selon la quantité de dimensions. Dennis Sullivan a développé un
outil qui permet de construire une variété à partir d’une autre de façon
contrôlée. Cet outil a été déterminant pour classer les variétés de
dimensions supérieures ou égales à 5. |
|
Exemples dans le domaine classique Ces ont les variétés des objets géométriques classiques. |
|
|
|
Exemples exotiques Certaines variétés présentent des propriétés
surprenantes. Voir Objets
topologiques |
|
|
|
Extension aux variétés
différentielles |
|
|
|
Pourquoi VARIÉTÉ
? Ce terme
signifie diversité ou multiplicité. C'est Bernhard Riemann qui a développé la notion
de variété pour généraliser les surfaces à des dimensions supérieures. Il leur donne le nom allemand: Mannigfaltigkeit
qui donnera Manifold en anglais (many folds => plusieurs plis). |
Une variété désigne tout espace qui se comporte
localement comme ℝn mais qui peut
avoir une structure globale très complexe. Le choix du mot variété s’explique par le fait
que les objets nommés sont des structures mathématiques qui peuvent avoir des
formes et des propriétés très différentes, tout en partageant la caractéristique
commune d’être localement similaires dans l’espace euclidien. En d’autres termes, les variétés forment une
famille de structures diverses, unifiées par leur définition mais possédant
une grande richesse de formes possibles. |
|
|
Le mot allemand
Mannigfaltigkeit désigne quelque chose qui possède une grande
diversité de formes ou de structure. Une notion parfaitement adaptée aux variétés
topologiques, qui peuvent être localement simples mais globalement complexes
et riches. |
Décomposition du mot mannig : signifie
"multiple" ou "varié." faltig : signifie
"pli" ou "structure pliée." Faltig" est souvent
utilisé pour exprimer une caractéristique répétitive ou une multiplicité de
formes. -keit : suffixe
équivalent à "-ité" en français. |
|
|
SIMPLES |
COMPLEXES |
|
|
Dimension : Les variétés les plus simples sont de dimension
1, comme une droite ou un cercle. Celles de dimension 2, comme le plan ou la sphère,
offrent déjà des formes plus sophistiquées. |
En dimension supérieure, on trouve des variétés
comme le tore ou des espaces plus abstraits utilisés en physique et en
mathématiques. |
|
|
Structure globale : Un cercle et une droite sont très différents. Globalement : la droite s’étend à l’infini, alors
que le cercle est fini et sans bord. |
Un tore (la forme d’un beignet) est plus complexe
que la sphère : il a un trou au milieu qui change son comportement topologique. |
|
|
Propriétés topologiques : Les variétés simples sont souvent connexes et
peuvent être simplement connexes (comme une sphère, pour laquelle toute
boucle peut être réduite à un point). |
Les variétés complexes, comme la bouteille de Klein,
peuvent avoir des propriétés inhabituelles, comme ne pas avoir d’orientation
définie. |
|
|
Bords Sans
précision, une variété topologique est censée être une variété sans bord. Voir Ouvert-fermé |
En rampant sur la surface d’un ballon (une sphère) ou d’un pneu (un tore), nous ne
sommes jamais arrêtés par une quelconque barrière. Ce sont des variétés sans bord de dimension 2. En se promenant dans le ballon (une boule), nous
sommes dans la dimension 3, et nous rencontrons un bord, la surface de la
boule (une sphère). Il est toujours possible de fabriquer des
variétés à bord en effectuant un ou plusieurs trous dans une variété sans
bord; la partie enlevée, comme la partie qui reste, devient une variété
topologique à bord. |
|
|
Sphère et boule |
Promenade dans une boule ouverte: nous ne
pourrons jamais atteindre aucun bord... En effet, une boule ouverte est une variété sans bord
de dimension 3 qui est d’ailleurs homéomorphe à R3. Par contre, une boule fermée est une variété à
bord de dimension 3, les points du bord sont ceux de la sphère (une variété
de dimension 2) et ils possèdent – dans la boule fermée – des voisinages particuliers.
|
|
|
Variété
différentiable |
||
|
Intuitivement, on peut considérer une variété
différentiable comme une variété topologique qui soit lisse, c’est-à-dire
sans plis, sans coins, etc. Deux notions pour travailler sur les variétés
différentiables: la carte et l'atlas.
|
Cela permet de caractériser et d'étudier la
géométrie locale en utilisant des outils bien connus dans l'espace euclidien,
tout comme une carte papier qui aide à s'orienter dans une ville. Ces concepts permettent ainsi de passer de l'étude locale (facilement appréhendée comme une petite fenêtre sur Image: l'atlas constitue le vêtement qui recouvre
la variété, assemblé à partir de nombreuses cartes locales parfaitement
ajustées les unes aux autres. Ces idées sont fondamentales pour aborder la
structure lisse des variétés en géométrie différentielle, et elles permettent
de "traduire" la complexité globale d'un espace en une succession
de morceaux locaux plus simples à analyser. |
|
|
|
|
|
Quantité de variétés: Dimension 3 : 105 Dimension 4 :
plusieurs millions |
Une variété de Fano est une
variété algébrique projective lisse connexe, définie sur un corps algébriquement clos, dont
le fibré anticanonique (c’est-à-dire le déterminant du fibré tangent) est ample. – Olivier Debarre |
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |