Nombre de Ramsey - Introduction

Édition du: 05/06/2023

INDEX Graphe Topologie Géométrie Logique Dénombrement Jeux	Nombres et théorème de RAMSEY
	Petits Nombres (Intro.)	Valeurs – Table	EN BREF – Tour d'horizon
	Principe des tiroirs	Propriétés et calculs	R(3, 3) = 6	R(3, 3, 3)
	Assemblée	Bornes – Historique	R(4, 3) = 9	R(5, 3) = 14
	Graphe	Ramsey – Biographie	R(4, 4) = 18

Faites un double-clic pour un retour en haut de page

NOMBRES de RAMSEY

Introduction – Débutant

Approche

Le principe des tiroirs dit que: si vous avez trois chaussettes à placer dans deux tiroirs, il y aura nécessairement un tiroir comportant au moins deux chaussettes. (Illustration)

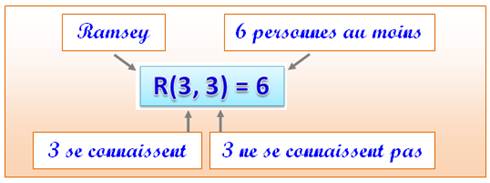
Plus incroyable, la théorie de Ramsey permet d'affirmer, par exemple, que parmi six personnes, il y aura nécessairement au moins trois personnes qui se connaissent mutuellement ou trois personnes qui ne se connaissent pas du tout.

Ou encore, si on colorie un hexagone et ses diagonales en rouge et en bleu, il est impossible d'éviter un triangle monochrome (rouge ou bleu).

Sommaire de cette page

>>> Une assemblée de six personnes

>>> Polygones à six sommets

>>> Polygones à neuf sommets

>>> Nombres de Ramsey

>>> Théorie de Ramsey

Débutants

Dénombrement

Glossaire

Combinatoire

Anglais : Ramsey numbers

Une assemblée de six personnes		haut
Curieusement, avec six personnes, pas plus, pas moins, il y aura nécessairement, au moins: trois personnes qui se connaissent toutes, OU trois personnes qui ne se connaissent pas du tout. On note R(3, 3) = 6 et on dit que le nombre de Ramsey (3,3) est 6.
Pour se convaincre, voyons les configurations possibles:	Il y a au moins trois qui se connaissent dans tous les cas où 6, 5, 4 ou 3 personnes se connaissent. Dans le cas contraire, il y 4 ou 5 ou 6 personnes qui ne se connaissent pas, donc, au moins, trois.

Voir Nombre R(3, 3) pour plus de détails

Polygones à six sommets

haut

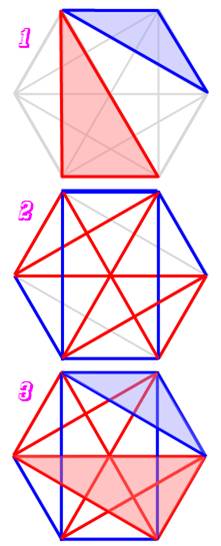
Avec une figure à six sommets

Ici un hexagone régulier muni de toutes ses diagonales. On dit qu'il est alors complet.
Il n'est pas nécessaire qu'il soit régulier.

1) Il est possible de tracer deux triangles de deux couleurs différentes, chacun ayant des sommets différents. Très bien.

Mais, le défi posé est le suivant: en coloriant toute cette figure avec deux couleurs, est-il possible de ne pas faire apparaitre de triangle d'une seule couleur (monochrome): soit rouge, soit bleu ?

2) Dans ce cas, la figure est presque complètement coloriée sans triangle monochrome. Il reste deux traits en gris.

Notez bien que les sommets des triangles sont les sommets de l'hexagone. Les points de croisement des arêtes ne sont pas des sommets et ne comptent pas.

3) Ici, en dessinant l'une des deux arêtes manquantes, en rouge ou en bleu, inévitablement, un triangle monochrome est créé.

Avec six sommets, mais pas cinq, un triangle monochrome est inévitable.

On note ce nombres de Ramsey: R(3, 3) = 6.

Coloration de l'hexagone complet

Voir Brève 50-996

Polygones à neuf sommets

haut

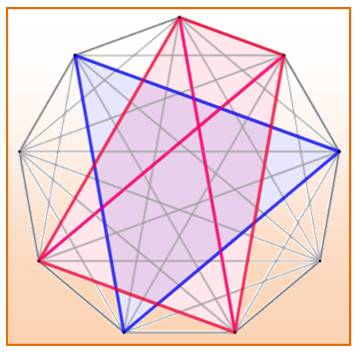
Dans le cas de neuf sommets (ici un ennéagone régulier), il est possible de faire cohabiter indépendamment un triangle et un quadrilatère complet (avec ses diagonales).

On montre que neuf sommets est le minimum pour construire l'une au moins de ces deux figures.

On note le nouveau nombre de Ramsey:

R(3, 4) = 9.

Remarque de vocabulaire

Un polygone complet est un polygone où sont dessinés tous les côtés et toutes les diagonales.

Ces polygones complets à n sommets sont notés: R_n

On peut alors dire qu'il possible d'implanter un R₃ ou un R₄ distincts dans un R₉.

Coloration de l'ennéagone complet

Les polygones complets monochromes (rouge ou bleu), internes à un plus grand polygone complet, sont parfois appelés CLIQUES.

Nombres de Ramsey			haut
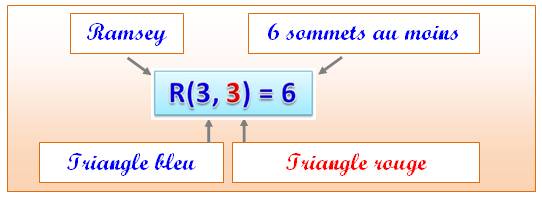
Nous venons de voir qu'il est nécessaire de disposer de six sommets pour dessiner deux triangles indépendants. Ce graphique résume la notation pour R(3, 3) = 6.
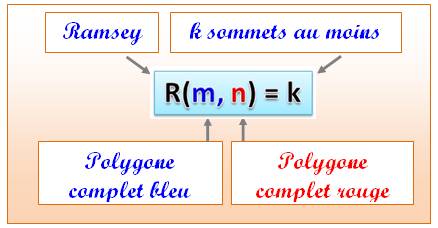
D'une manière générale, le nombre de Ramsey R(m , n) est la quantité k de sommets nécessaire et suffisante pour que l'un des deux polygones complets bleu ou rouge existe inévitablement dans un polygone de k sommets. Notez que l'on s'intéresse à des polygones de deux couleurs seulement.

Théorie de Ramsey		haut
Importance Les nombres de Ramsey sont utilisés principalement en combinatoire et théorie des graphes. Ils sont à l'origine de toute une théorie: la théorie de Ramsey. Les nombres de Ramsey créent un pont entre la combinatoire, la probabilité et la géométrie. En fait, les nombres de Ramsey sont très difficiles à calculer. Dès le niveau 5, on ne sait ni calculer ni raisonner pour trouver le nombre de Ramsey. On sait simplement l'encadrer: R(5, 5) est compris entre 43 et 48, par exemple.	Recherches De tout temps, les mathématiciens ont cherché à cerner ces nombres de Ramsey. On connait aujourd'hui des inégalités bornant les nombres de Ramsey: générales pour R(m, n) quelconque, ou spécifique pour m et n donnés. Gros progrès réalisé en mars 2023 par Julian Sahasrabudhe, Simon Griffiths et Marcelo Campos qui ont réussi à minimiser significativement la borne supérieure des nombres de Ramsey.
Nombre de Ramsey en général Le nombre de Ramsey R(m, n) est le nombre minimum de sommets nécessaires pour qu'un graphe contenant un nombre arbitraire d'arrêtes comporte soit m sommets tous reliés entre eux soit n sommets tous non reliés entre eux. Une autre formulation dit que le nombre de Ramsey est le nombre R(m, n) de personnes qu'il faut inviter pour que m personnes se connaissent toutes entre elles ou que n personnes ne se connaissent pas entre elles.	Nombre de Ramsey en théorie des graphes Dans le langage de la théorie des graphes, le nombre de Ramsey est le nombre minimum de sommets v = R(m, n) tel que tous les graphes simples non orientés d'ordre v contiennent une clique d'ordre m ou un ensemble indépendant d'ordre n. Le théorème de Ramsey stipule qu'un tel nombre existe pour tout m et n.

Haut de page (ou double-clic)

Retour	Principe des tiroirs
Suite	EN BREF – Tour d'horizon sur les nombre et la théorie de Ramsey
Voir	Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index Logique formelle Percolation Relier les points d'un seul coup de crayon Topologie – Glossaire Tour de Brahmâ	Trois maisons (énigme des -) Coloration des graphes (nombre chromatique) Graphe planaire Petit monde Quatre couleurs Sept amis autour d'une table Vocabulaire des graphes Coloration des graphes Nombres et couleurs
Sites	Théorème de Ramsey – Wikipédia Théorème de Ramsey – Bibm@ath Ramsey numbers – Wolfram Mathworld Ramsey's Numbers – Cut-the-Knot – Accès à toutes les pages *Théorie de Ramsey – Thomas Budzinski – 2022 – 16 pages Théorème de Ramsey – Coloration de graphes – Mathraining Ramsey Theory – Lane Barton IV – 2016 A Very Big Small Leap Forward in Graph Theory – Quanta Magazine – Leila Sloman – 2023** et autres articles annonçant cette nouvelle OEIS A212954 – Triangle read by rows: T(n,k) = R(r,s) (two color Ramsey numbers) Ramsey Theory 2 – math.caltech.edu – Adam Sheffer
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaRamse/Introduc.htm