|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Niveau terminale = compréhensible par un élève de
terminale
![]()
|
INVERSION avec le CERCLE Démonstrations L'inversion est un outil mathématique bien utile.
Il est parfois plus facile de raisonner sur l'inverse d'une figure que sur la
figure elle-même. Outil très utile pour réaliser certaines démonstrations
ou certaines constructions. Analogie Les nombres
complexes vous envoie dans le monde imaginaire pour y résoudre un
problème et vous renvoie dans le monde réel avec la solution. Même effet avec
l'inversion qui vous fait passer dans un monde où la solution s'avère
abordable puis, revenir par l'inversion inverse dans le monde initial avec la
solution en poche. Un minimum de connaissances
sur les inversions est utile pour aborder cette page. |
|
|
||
|
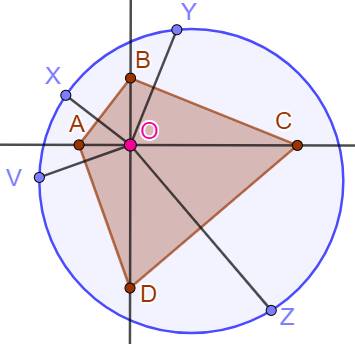
Problème Un
quadrilatère ABCD dont les diagonales sont perpendiculaires. Les
quatre points symétriques de O par rapport aux côtés. Monter
que les quatre points-images sont cocycliques. Principe Comment quatre cercles passant
par un point forment un rectangle par inversion Le rectangle est toujours inscriptible
dans un cercle |
|
|
|
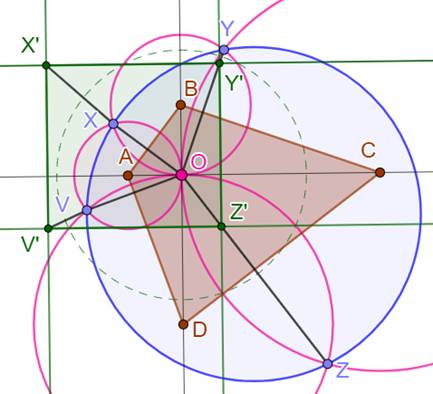
On se donne Une inversion de
centre O et de puissance arbitraire (vert pointillé). Les quatre
cercles passant par O et deux des points réfléchis X, Y, Z, V (roses). Démonstration Les cercles,
passant par 0, sont inversés en droites perpendiculaires aux rayons OA, OB,
OC et OD, délimitant ainsi un rectangle. Les points X, Y,
Z et V, chacun intersections de deux cercles se retrouvent en X', Y', Z' et
V', intersections de deux droites (l'inversion conservent les intersections. Ces points sont
les sommets du rectangle X'Y'Z'V'. Or, le rectangle est inscriptible dans un
cercle. Son image XYZV par inversion l'est aussi. |
Représentation de l'inversion
utilisée
Cercle directeur de l'inversion
en vert pointillé. Cercles à inverser en rose. Droites images de l'inversion en
vert. Note: la construction de l'inversion n'est pas utile. Elle sert à se rassurrer.
Pour la construire simplement, souvenez-vous que le cerle et son image se
coupent aux mêmes endroits. Ci-dessus, trois cas faciles pour B, C et D; pour
A, il faut construire l'inversion. |
|
|
Arbelos ou tranchet du cordonnier |
|
||
|
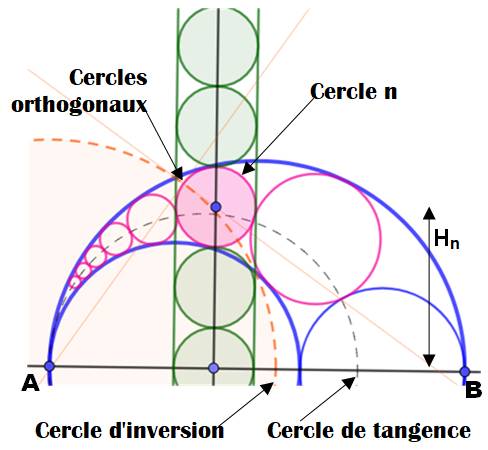
Problème On part
des trois demi-cercles bleus et on construit les cercles tangents dans
l'espace entre les deux plus grands. Montrez que
les points de tangence sont sur le même cercle. Montrer
que la hauteur Hn du centre du
cercle n est égale à n fois le diamètre de ce cercle |
L'inversion transforme le croissant
des cercles différents en une pile de cercles identiques. Exemple avec le
cercle n= 3.
|
||
|
Inversion Centre
d'inversion en A Cercle
directeur tel qu'il soit orthogonal au cercle n (petites lignes en orange). Alors, le
cercle n (coloré en rose) est
invariant avec l'inversion. |
Explications Les deux demi-cercles bleus passant par A sont transfomés
en droites perpendiculaires à AB, donc parallèles. Le cercle n est tangent aux deux cercles bleus; son image
(lui-même) est tangent aux images des cercles bleus, les deux parallèles. Toutes les cercles intermédiares conservent leur point de
tangence et s'enfilent entre les deux parallèles. La figure montre que Hn = n .Dn (ici H3 = 2 Dn) La ligne centrale noire passe par tous les points de
tangence des cercles verts; elle se transforme en cercle par lequel passe
tous les points de tangence des cercles roses (pointillé noir). |
||
Voir Aire
de l'arbelos / Anglais Pappus chain and shoemaker's knife) / Sangakus
|
|
||
|
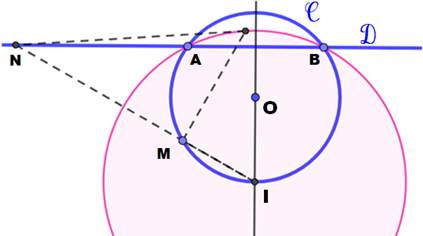
Inversion
avec cercle directeur de centre I et de rayon OA. Dans
cette configuration, la droite D passant par la corde AB est l'inverse du
cercle C, passant par I, le centre d'inversion. On montre la construction de
l'inverse de M en N pour se rassurer. |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()