|
|||||||||||||||||||||||||||||||||||||||
![]()
|
CONJECTURES de POLIGNAC et voisines Deux conjectures à l'actif
d'Alphonse de Polignac
(1826-1863), mathématicien français; formation: Polytechnique; spécialité:
théorie des nombres. La première est une
généralisation de la conjecture sur la quantité infinie des nombres premiers jumeaux. Pas
prouvée. La seconde, en mimétisme
avec celle de Goldbach, affirme que tout nombre
impair est la somme d'un nombre
premier et d'une puissance de 2.
Elle est fausse dès le nombre
137. |
Voir Contemporains de Polignac
|
|
||
|
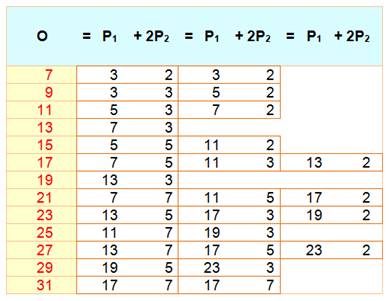
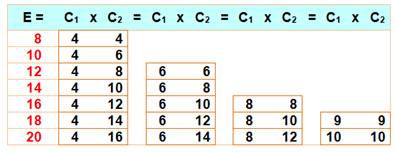
Conjecture Tout nombre pair est égal à la
différence de deux nombres premiers consécutifs d'une infinité de manières. Formulation E = Pn – Pn+1 |
Autres formulations
Etc. |
|
|
Exemples de 2 à 20 (il s'agit bien de premiers consécutifs, aucun premier entre
les deux)
Point de la situation: trois conjectures 1. Conjecture de Chen:
il existe une infinité de paires de premiers avec une différence égale à K. 2. Conjecture de Polignac:
idem Chen, mais avec paire de premiers consécutifs. 3. Conjecture des premiers jumeaux:
Idem Polignac, avec K = 2. Ce que l'on sait
|
||
Nombre premier noté P; nombre pair , noté E comme Even;
impair noté O comme Odd;
|
|
||
|
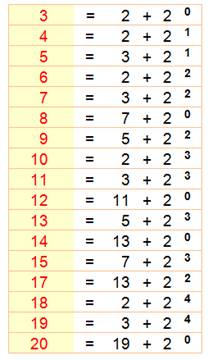
Conjecture Tout nombre impair est égal à la
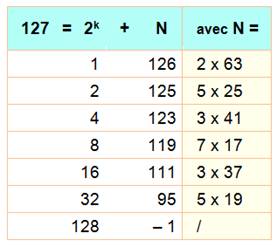
somme d'un nombre premier et d'une puissance de 2. Elle n'est vraie que jusqu'à 127. Avec les nombres pairs,
elle s'arrête dès le nombre 16. Historique
Valeurs hors conjecture jusqu'à 1000 127, 149, 251, 331, 337, 373, 509, 599, 701, 757, 809,
877, 905, 907, 959, 977, 997. Exploration
|
Formulation O = P + 2k Exemples de 3 à 20 pour
tout nombre (pairs et impairs)
Le nombre 16 est le premier nombre pair manquant. Cas de 127
N est toujours composé. |
|
|
|
||
|
Conjecture Tout nombre impair supérieur ou
égal à 7 est égal à la somme d'un nombre premier et d'un autre doublé Formulée en 1775 par Lagrange. Reprise en 1963 par Lévy. Nombres pairs Seul E = 2 + 2 x P
répond à la conjecture. Comme: 6 = 2 + 2x2 8 = 2 + 2x3 12 = 2 + 2x5 16 = 2 + 2x7 … Les nombres 10, 14, 18, 20, 22, 26, 30, 32, 34, 38 … ne
sont pas accessibles. |
Formulation O = P + 2.P Exemples de 7 à 31
|
|
|
|
||
|
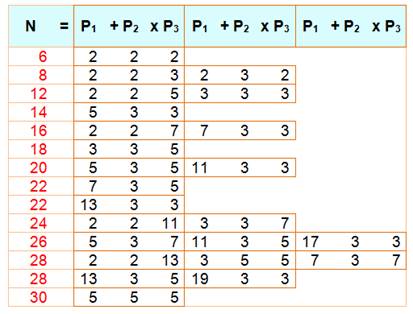
Théorème de Chen Il s'applique aux nombres pairs (1) Tout nombre pair suffisamment grand
est égal à la somme d'un nombre premier et du produit de deux nombres
premiers
Il semble que cela marche à partir de 12. Nombres impairs (2)
7 = 3 + 2x2 9 = 3 + 2x3 = 5 + 2x2 11= 2 + 3x3 = 5 + 2x 3 = 7 + 2x2 Cas particulier de Lagrange-Levy
Généralisation Conjecture de Zumkeller-Lebl (3) Tout nombre suffisamment grand est égal à un premier et
un produit de premier, avec un seul premier pouvant être égal à 2. |
Formulation E = P + P.P Exemples de 7 à 31
Départ à 12; en effet, le 10 est absent. Même conjecture mais avec le signe moins (4) N = P – P.P N La
relation semble vraie pour tout nombre. Exemples 1 =
7 – 2x3 2 = 17 – 3x5 =
23 – 3x7 3 =
7 – 2x2 = 13 – 2x5 4 =
19 – 3x5 = 37 – 3x11 5 =
11 – 2x3 = 19 – 2x7 6 =
41 – 5x5 = 61 – 5x11 7 =
11 – 2x2 = 13 – 2x3 87 = 101
– 2x7 = 113 – 2x13 |
|
|
|
||
|
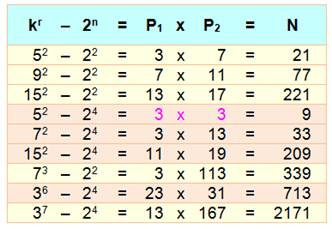
Conjecture Quels que soient n et r, il existe une infinité de nombres k tels que
N = kr – 2n est un nombre semi-premier, produit de deux
premiers distincts
|
Formulation
Exemples: quelques valeurs de k pour r et n donnés
Des
configurations en doublement du nombre premier (exemple ici avec 3x3) existent. La conjecture n'en a pas besoin. |
|
|
|
||
|
Théorème Tout nombre pair > 12 est la
somme de deux nombres composés.
|
Formulation E = C + C E > 12 Exemples
Pairs et impairs L'exploration montre que le premier pair est 8 et
le premier impair est 13. À partir de 12, tous les nombres semblent être
somme de deux composés distincts ou non. Exemple: 12 = 4 + 8; 13 = 4 + 9; 14 = 6 + 8; 15 = 6 + 9 … |
|
|
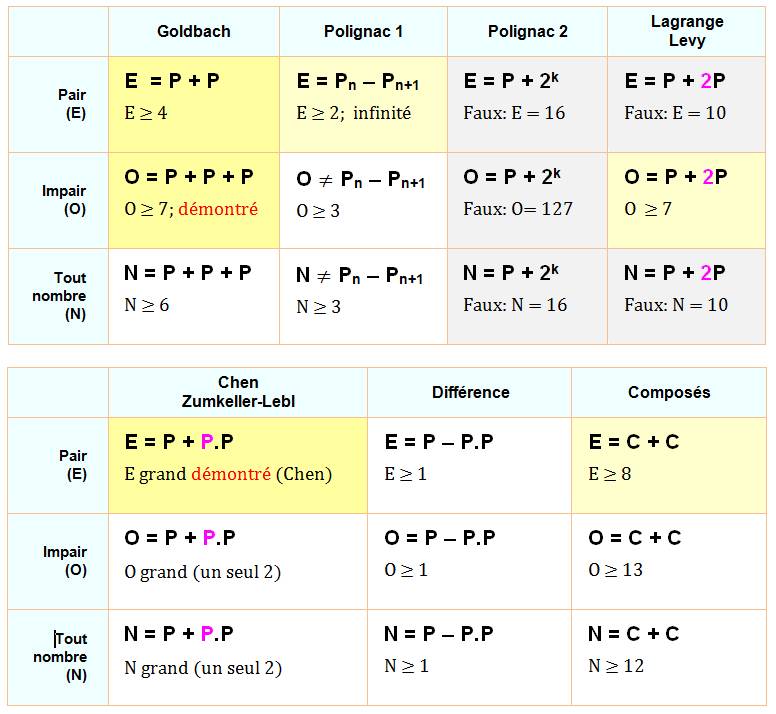
Malgré
de fortes présomptions de véracité pour toutes ces conjectures, seules deux
d'entre elles sont démontrées:
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()