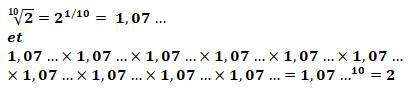|
Édition du: 14/10/2020 |
|
INDEX |
CALCUL – Technique opératoire |
|||
![]()
|
Opérations avec 10 Complément à 10 La maitrise du
complément à 10 s'acquiert à l'école primaire.
Il est très utile pour la résolution rapide de nombreuses opérations. |
|||
|
|
Sommaire de cette page >>> Addition et
soustraction >>> Complément à 10 >>> Soustraction avec c. à
10 >>> Multiplication |
>>> Division >>> Puissance >>> Racine >>> Logarithme >>> Trigonométrie |
Débutants Glossaire |
|
Ajouter dix,
c'est augmenter les dizaines d'une unité. |
23 + 10
= 33 123 + 10 = 133 |
180 + 10 = 190 190 + 10 = 200 |
|
|
Soustraire dix,
c'est diminuer les dizaines d'une unité. |
23 – 10
= 13 123 – 10 = 113 |
190 – 10 = 180 200 – 10 = 190 |
|
|
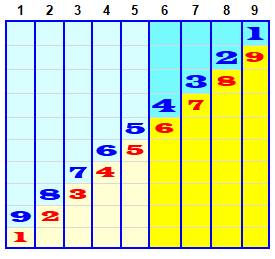
Approche Le tableau montre les nombres n de 1 à 9 et leur
complément à 10 (c). Autrement-dit: la somme du nombre et de son
complément à 10 vaut 10: n + c =
10 Définition Le complément à 10 de n est le nombre à ajouter à
n pour faire 10. Exemples Le nombre 2 est le complément à 10 du nombre 8 et réciproquement, 8
est le complément à 10 de 2. Anglais
|
9 + 1 = 10, 8 + 2 = 10, etc. Les plus utiles seront les compléments à 10 des nombres de 6 à 9. |
||
|
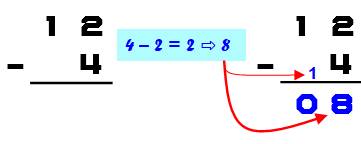
Principe Le complément à 10 facilite grandement la soustraction. Notez qu'avec
la pratique, chacun développe sa propre tactique. Voici un exemple (illustration). 1.
Pour faire 4 ôté de 2, faire l'opération à l'envers: 4 – 2 = 2; 2.
Prendre le complément à 10. C'est
8; 3.
Posez 8 comme résultat de cette soustraction; et 4.
Mettre une retenue de 1 pour les dizaines. |
Avec l'habitude, cette opération est immédiate, sans utiliser cet
artifice du complément. Mais, son principe est utile pour les soustractions plus compliquées. |
|||
|
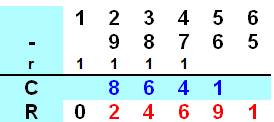
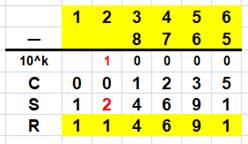
Soustraction avec compléments à 10 Pour cette soustraction, le complément à 10 est en action. La ligne bleue supplémentaire (C) indique les compléments à 10 lorsque
nécessaire. Avec l'habitude, elle devient mentale.
|
|
|||
|
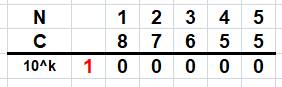
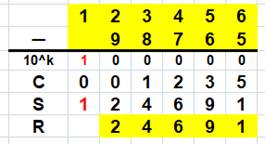
Soustraction avec compléments à 10k Pour réaliser ce type de soustraction encore plus rapidement et de manière
amusante, on va utiliser une généralisation du complément à 10, le complément
à 10k, lequel tient compte de la
propagation de la retenue. Il se forme en prenant:
La somme est une puissance de 10. Elle compte autant de "0"
que de chiffres dans le nombre à complémenter. |
Ici 10^k = 10k vaut 100 000 avec k = 5, autant de
"0" que de chiffres dans 12 345, le nombre à complémenter. |
|||
|
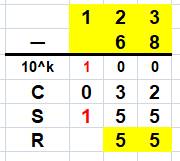
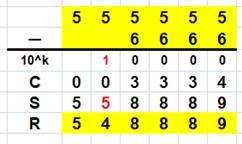
Soustraction rapide Il est amusant et assez simple d'effectuer une soustraction en
additionnant le complément: 1.
Ligne avec 10k avec k = 2 car 68 a deux chiffres; 2.
Ligne C avec le complément; 3.
Ligne S avec complément + le nombre du haut; 4.
Ligne R: soustraction du 1 de la puissance de 10. |
|
|||
|
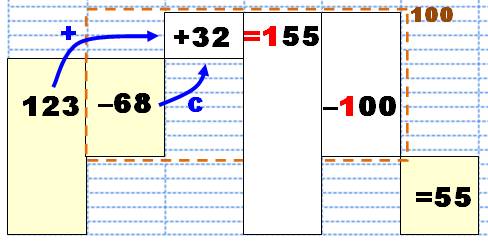
Résumé de la méthode Pour effectuer 123 – 68: 1.
Complément de 68 à 100 = 32; 2.
L'ajouter à 123 (= 155); 3.
Déduire la puissance de 10; 4.
Résultat: |
|
|||
|
Exemples de soustractions
|
||||
Voir Calcul
mental avec la soustraction
Merci à Kevin Martin pour
ses remarques
|
Multiplier par dix c'est décaler le nombre d'un cran vers la
gauche: c'est-à-dire: en ajoutant un zéro, ou en déplaçant la virgule. |
5 x 10
= 50 50 x 10
= 500 100 x 10 = 1 000 123 x 10 = 1 230 |
12,3 x 10 = 123,0 1,23 x 10 = 12,3 0,123 x 10 = 1,23 0,0123 x 10 = 0,123 |
|
|
Multiplier par 5 c'est multiplier
par 10 et diviser par 2. |
123 x 5 = 1 230 / 2 = 615 987 x 5 = 9 870 / 2 = 4 935 |
||
|
Diviser par dix
c'est décaler le nombre d'un cran vers la droite: |
50 / 10
= 5 100 / 10
= 10 1 000 / 10 = 100 |
123 / 10
= 12,3 12,3 / 10
= 1,23 1,23 / 10
= 0,123 0,123 / 10 = 0,0123 |
|
|
Diviser par 5 c'est diviser par 10
et multiplier par 2. |
1 230 / 5 = 123 x 2 = 246 9 870 / 5 = 987 x 2 = 1 974 |
||
|
Élever un nombre à la puissance
dix c'est multiplier ce nombre dix fois
par lui-même. Dix à la puissance dix est un nombre formé par un 1 suivi de dix
zéros. |
110
= 1 210
= 1 024 310
= 59 049 410
= 1 048 576 510
= 9 765 625 610
= 60 466 176 710
= 282 475 249 810
= 1 073 741 824 910
= 3 486 784 401 1010
= 10 000 000 000 |
|
|
La racine dix d'un nombre N est le nombre n qui multipliée
dix fois par lui-même donne le nombre initial N.
Racine dixième de 1 024 est égale à 2, car 210
= 1 024. Racine dixième de dix milliards
vaut 10.
|
|
|
|
Le logarithme
en base dix du nombre dix vaut 1; Exponentielle
10, c'est e élevé à la puissance
10, |
Log10 (10) = 1 ln (10) = 2,302585093… e10 = 22026,46579… |
|
|
Rappel: le sinus
d'un petit angle est proche de sa valeur en radians;
de même pour la tangente. |
10° = 0,1745329252 radian Sin (10°) = 0,1736481777… Cos (10°) = 0,9848077530… Tan (10°) = 0,1763269807… |
|
![]()
|
Retour |
||
|
Suite |
|
|
|
Sites |
|
|
|
Cette page |
||