![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page |
|
22 Novembre 2025
![]()
|
Édition du: 29/11/2025 |
|
INDEX lettre R |
Dictionnaire de base du vocabulaire des mathématiques |
|
|
Faites
un double-clic pour un retour en haut de
page
Pour
trouver un mot: Ctrl F et tapez le mot
cherché
|
Avertissement Dictionnaire pour débutants,
juniors, novices, "nuls" … !!! On privilégie la compréhension par rapport à une rigueur mathématique !!! Les liens permettent de compléter et d'approfondir Pour une
version plus académique se reporter aux ouvrages spécialisés |
Légende Parfois,
plusieurs définitions sont données: de la plus "intuitive" à la
plus correcte mathématiquement. Mode de recherche: si vous ne trouvez
pas symétrie centrale à symétrie, voyez à centrale, par exemple. Difficulté: * notion avancée;
** notion complexe. |
![]()

R en fonte éclaircie:
![]() est l'ensemble des nombres réels.
est l'ensemble des nombres réels.
Tous les nombres de toute nature: entiers, rationnels, irrationnels,
transcendants.
Un nombre réel est un nombre qui peut être représenté par une partie entière et
une liste finie ou infinie de décimales.
L'ensemble des nombres réels est un corps.
–
v. Tous les types
de nombres
– a.
Real number
Racine carrée: nombre réel positif, noté ![]() , qui multiplié par
lui-même donne a.
, qui multiplié par
lui-même donne a.
– ex. ![]() , car 9 x 9 =81;
, car 9 x 9 =81;
Tout nombre réel
positif a deux racines carrées: ![]() , et
, et ![]()
Tout nombre réel négatif a deux racines carrées imaginaires: ![]() , et
, et ![]()
– notation en puissance
fractionnaire: ![]() .
.
– notez que l'on dit extraire une racine,
comme la racine d'un végétal enfouie en terre.
– propriétés: ![]() ;
; ![]()
![]()
– v. Racines carrées – Index, radical
– a. Square root
Racine cubique: nombre réel positif, noté ![]() , qui multiplié par
lui-même trois fois donne a.
, qui multiplié par
lui-même trois fois donne a.
– ex. ![]() , car 3 x 3 x 3 = 27.
, car 3 x 3 x 3 = 27.
– a. Cubic root
Racine énième: la racine nième
suit le même schéma, Elle est notée ![]() .
.
Un nombre possède n racines nièmes réelles ou complexes.
– notation en puissance fractionnaire ![]()
– v. Racines
– a. nth root, fourth root, fifth root, etc. The computation of an nth root is
a root extraction.
Racine d'un polynôme, d'une
équation: valeur de l'inconnue.
– ex. x – 4 = 0, alors 4 est la
solution, appelée la racine.
La racine d'un polynôme est la solution de l'équation lorsqu'on le compare à
zéro: (P(x) = 0).
Dans le cas des fonctions, on préfère parler du zéro
de la fonction.
– v. Équations, résolution,
solution, zéro, inconnue, théorème fondamental de
l'algèbre
Théorème
fondamental de l'algèbre ou théorème de d'Alembert-Gauss: tout polynôme non constant, à
coefficients complexes, de degré n a exactement n racines, chacune étant
comptée avec son ordre de multiplicité.
The fundamental theorem of algebra (the
d'Alembert-Gauss theorem) is stated as follows: every non-zero,
single-variable, degree n polynomial with complex coefficients has, counted
with multiplicity, exactly n complex roots.
Racine évidente (théorème de la -) : possibilité de
trouver immédiatement les racines d’un polynôme en observant ses coefficients
extrêmes.
– v. >>>
– a. Rational root theorem.
Racine numérique d'un nombre ou résidu: le chiffre unique obtenu par le procédé de
la preuve par neuf.
Additions itératives des chiffres pour obtenir un résultat à un seul chiffre.
La quantité d'itérations est la persistance additive du nombre.
– ex. Pour le nombre 789: 7 + 8 + 9 = 24 et
2 + 4 = 6; sa racine additive est 6 et sa persistance est 2.
– v. Racine numérique et
persistance additive, persistance
multiplicative
– a. Digital root, digital sum, additive persistence of a number.
Digital product of a number,
multiplicative persistence of a number.
The digital root is the single-digit value
obtained by an iterative process of summing digits.
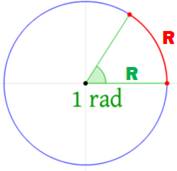 Radian (rad): unité de mesure des
angles;
Radian (rad): unité de mesure des
angles;
Un tour complet vaut 2![]() = 6,28 … radians.
= 6,28 … radians.
Un angle de 1 radian intercepte un arc de longueur égale à celle du rayon du
cercle (Illustration).
– Unité SI, notée rad.
Notation le plus souvent non indiqué: ![]()
– conversion: 1 radian = 180 / ![]() = 57,2957795130…°
= 57,2957795130…°
– v. Radian, table de
conversion des angles
– a. Radian
Radical: désigne le symbole
de la racine ![]() .
.
– ex. dans ![]() le radical est d'ordre 3. On peut aussi
utiliser la notation
fractionnaire: 81/3.
le radical est d'ordre 3. On peut aussi
utiliser la notation
fractionnaire: 81/3.
L'expression sous le radical est le radicande.
– v. Racine, calcul par programme, vinculum
– a. Surd, radicand
Radical "usuel" du nombre entier n
positif: la racine
carrée positive de n.
L'expression sous le radical est le radicande
(mot peu utilisé) et le trait horizontal au-dessus est le vinculum
(pas plus utilisé !).
Radical indicé: ![]() désigne la racine
positive kième de n.
désigne la racine
positive kième de n.
– a. ![]()
Radical imbriqué: des "racines de racines" comme: ![]()
–
v. Radical imbriqué
– a.
Nested radical
Radical d'un nombre entier: le produit de ses facteurs
premiers (sans leur multiplicité).
– ex. 100 = 22 x 52 et
r(100) = 2 x 5 = 10.
– v. Radical d'un nombre, nombre entier
– a. Radical of an integer: the product of the distinct prime numbers dividing
n.
Radical (ou racine) d'un idéal** Le radical d'un idéal I dans un
anneau commutatif A est l'ensemble des éléments de A dont une
puissance appartient à I.
– a. Radical of an ideal
Le radical de Jacobson** d'un anneau
commutatif est l'intersection de ses idéaux maximaux.
– a. Jacobson radical
Axe radical de deux cercles: ensemble des points de même puissance par
rapport à deux  cercles.
cercles.
– v. Axe radical
Point radical: même puissance par rapport à trois cercles.
– v. Point radical (Illustration)
– a. Radical point
Raison: équivalent à
progression élémentaire (incrément) en parlant d'une suite (progression).
Quantité à ajouter pour une suite
arithmétique ou par laquelle il faut multiplier dans une série géométrique.
–
ex. 123 + 333 = 456 et 456 + 333 = 789, la raison est 333
– a. Common difference
Raisonnement: cheminement de
pensée qui partant de propositions en déduit d'autres propositions avec leur
valeur de vérité..
– v. Raisonnement,
logique, syllogisme
Raisonnement déductif: du général au particulier.
Raisonnement inductif: du
particulier au général.
– v. Types
de démonstrations
– a. Deductive reasoning, inductive reasoning
Raisonnement par récurrence ou par
induction: de type inductif, il consiste à s'appuyer sur un point de départ qui
est vrai, et à démontrer que la propriété est vraie pour tout successeur, alors
elle est toujours vraie.
– v. Récurrence
– a. Mathematical induction
Raisonnement par l'absurde: démonstration avec une hypothèse contraire à ce
que l'on veut démontrer et déboucher sur une contradiction. L'hypothèse n'était
donc pas adéquate.
– v. Raisonnement
par l'absurde
– a. reductio ad absurdum or argumentum
ad absurdum, proof by contradiction, indirect proof
Rang d'un chiffre dans
un nombre: autre terme pour dire position.
Le rang ou la position d'un chiffre dans un nombre indique la puissance de dix
qui est sous-entendue pour écrire ce nombre sous forme abrégée.
– ex. 1234 sous forme "dépliée" donne 1 × 1000 + 2 × 100 + 3 × 10 + 4; le 2 est en troisième position ou au 3e
rang et la puissance de dix associée est mille (103).
On dit que nous comptons avec un système de numération de position.
– v. Système décimal
– a. Digit position, place value
The numerals used in
denoting a number take different place values depending upon position
Rang d'une courbe elliptique**: nombre qui donne la quantité minimale de
points rationnels qui conduisent à la construction de tous les points
rationnels de la courbe.
– v. Rang d'une coure
elliptique
– a. Rank of the elliptic curve
Rangement:
si x>1 alors: 1 < ![]() x < x < x² < x3 …
x < x < x² < x3 …
si 0<x<1 alors: 0 < … < x3 < x² < x < Öx < 1
– v. Inégalité.
 Rapport: synonyme de
fraction et de quotient.
Rapport: synonyme de
fraction et de quotient.
Coefficient de grossissement, de changement d'échelle.
– v. Rapport, proportion, prorata
– v. Fraction, règle de trois, multiplication
– a. Ratio: The relative magnitudes of two quantities (usually expressed as a quotient).
Rapport d'homothétie, de similitude: facteur de grossissement.
Rapport entre une mesure d'un segment sur l'image à la mesure du même segment
sur la figure initiale.
– v. Homothétie
– a. Ratio of the homothety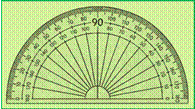 , ratio of similarity
, ratio of similarity
Rapporteur: instrument pour mesurer les
angles (Illustration).
– a. Protractor: A protractor is a handy tool used to measure and draw angles.
Ratio: synonyme de
rapport, division, exprimé en général en pourcentage.
–
étym.. ratio en latin veut dire, entre autres: calcul (rationem puta: tout calcul fait), compte
(rationem et numerum habere: avoir le
compte et le chiffre exact), raison (necesssaria
mathematicorum ratione concludere: arriver à la conclusion par la rigueur
d'un raisonnement mathématique).
– v. Rapport, proportion, prorata, fraction,
règle de trois,
multiplication
– a. Ratio
Ratio d’aspect: il décrit la
relation entre la largeur et la hauteur d’une image, qui est d’ailleurs liée
directement à la largeur et la hauteur du capteur.
– ex. si le capteur de l'appareil photo mesure 36 mm de large et 24 mm de
hauteur, son rapport hauteur/largeur, soit son ratio d'aspect, sera de 3:2 (et
non 36 mm x 24 mm ou 36:24; la fraction est réduite).
Rationnel: nombre qui peut
s'exprimer sous la forme d'une fraction.
Quotient de deux entiers relatifs n = p/q ave q non nul.
Avec q = 1, le nombre rationnel est un nombre entier.
Ensemble noté ![]() .
.
– v. Nombre
rationnel, types de
nombres
– a. Rational number: a number that can be expressed as the quotient or
fraction p/q of two integers
Rationnelle (fonction -): fraction algébrique
dont le numérateur et dénominateur sont des polynômes.
La fonction est propre si le degré du numérateur est inférieur à celui
du dénominateur.
–
notation: ![]()
– v. Fonction.
– a. Rational function: both the numerator and the denominator are
polynomials.
Rayon: segment joignant le centre d'un cercle à un point
du cercle; demi-diamètre.
Désigne aussi sa longueur.
–
a. Radius: any of the line segments from its center to its perimeter
Rayon-vecteur
ou vecteur position: dans le système de coordonnées
polaires, coordonnée notée ![]() qui représente la distance à
l'origine; l'autre coordonnée étant l'angle
qui représente la distance à
l'origine; l'autre coordonnée étant l'angle ![]() .
.
– v. Vecteur position
– a. Radius vector
 Rebroussement (point de -) ou cuspide: point singulier sur
une courbe avec changement de direction.
Rebroussement (point de -) ou cuspide: point singulier sur
une courbe avec changement de direction.
– a. Cusp
Recherche
opérationnelle: discipline dédiée aux méthodes scientifiques utilisables pour élaborer de
meilleures décisions.
Elle permet de rationaliser, simuler et optimiser l'architecture et le
fonctionnement des systèmes de production ou d'organisation.
Le problème du voyageur de
commerce en est un exemple.
– a. Operations research (U.-K. Operational research); often shortened to the
initialism OR.
Recette ou réception: c’est l’opération
par laquelle le client reconnaît que le produit livré par le fournisseur est
conforme à la commande passée, et qu’il est bon pour mise à disposition des
utilisateurs.
La recette est effectuée en présence du client et selon un protocole qui
respecte le cahier des charges (les spécifications du produit).
– v. Coder, déboguer, programme
– a. Accept, accepting, acceptance means approval or agreement, aceptance
is the final testing performed once the functional, system and regression
testing are completed; coding, testing, debugging
Réciproque
(énoncé, proposition -): tous les corbeaux sont noirs, mais la réciproque
n'est pas vraie: tout ce qui est noir n'est pas un corbeau.
La réciproque du théorème de
Pythagore est vraie.
Une implication réciproque est une proposition
interchangeant la prémisse et la conclusion d'une
implication.
– v. Énoncé direct, théorème, contraposée
– a. Converse: the result of reversing its two constituent statements.
|
Réciproque de: |
si A alors B ⇨ |
si B
alors A |
|
Contraposée
de: |
si
non B, alors non A |
Si la propriété est vraie,
la réciproque peut être vraie ou fausse;
La contraposée est toujours vraie.
Exemple amusant: si cet animal est l'homme
alors l'animal peu parler.
Réciproque: si cet animal peut parler, alors c'est l'homme. Faux ! Et le
perroquet.
Réciproque d'un théorème: un théorème propose
une conclusion à partir d'hypothèses. Sa réciproque conclut aux hypothèses à
partir de la conclusion.
La réciproque du théorème de Pythagore énonce que si a² = b² + c² alors le
triangle est rectangle.
– a. converse of a theorem.
En anglais the reciprocal of the Pythagorean
theorem énonce que 1/b + 1/c = 1/h, ave h la hauteur.
Réciproque (proposition -): proposition directe
A implique B et sa fonction réciproque B implique A.
– ex. réciproque du théorème
de Pythagore: si dans un triangle a² +b² =
c², alors le triangle est rectangle.
– v. Implication
Bijection réciproque ou fonction
réciproque: fonction directe y = f(x) et sa fonction réciproque x = f-1(y).
C'est l'application qui associe à chaque élément de l'ensemble d'arrivée son
unique antécédent par f.
– ex. fonctions exponentielles
et logarithmes ou
encore l'élévation au carré et la racine
carrée, mais sur les entiers positifs.
– a. Inverse function
Réciproque (relation -): La relation R d'un
ensemble A vers un ensemble B; sa relation réciproque R-1 associe
ses antécédents dans A à tout élément de B (s'ils
existent).
Réciprocité quadratique: La loi de
réciprocité quadratique décrit la possibilité d'exprimer un nombre premier
comme un carré modulo un autre nombre premier.
– v. Résidu quadratique, quadratique
– a. Quadratic reciprocity
Triplets de Pythagore réciproques: relation avec la
somme des inverses des carrés: 1/a² + 1/b² = 1/c².
– v. Triplets de Pythagore
réciproque
– a. reciprocal Pythagorean triple
Rectangle: quadrilatère avec
côtés perpendiculaires deux à deux.
Parallélogramme
dont les côtés opposés sont égaux deux à deux.
Les diagonales sont égales et se coupent en leur milieu.
Le rectangle a deux axes de symétrie et un centre de symétrie.
– v. Rectangle, types de quadrilatères
– a. Rectangle: A rectangle is a 2D shape in geometry, having 4 sides and 4
corners. Its two sides meet at right angles. Thus, a rectangle has 4 angles,
each measuring 90 ̊. The opposite sides of a rectangle have the same
lengths and are parallel.
Rectangle (triangle -): triangle dont l'un
des angles est droit.
Il peut être isocèle (deux côtés égaux) ou scalène
(côtés inégaux).
– v. Triangle rectangle
– a. A right triangle has one right angle. It may be isosceles
or scalene.
Rectangle (trapèze -): trapèze dont l'un
des angles est droit.
– a. Right
trapezoid
Rectangle (produit): comme on dit le carré de a pour, implicitement, l'aire d'un carré de côté
a, pour un rectangle de côtés c et d, on dit le rectangle
c.d pour le produit c.d qui représente l'aire du rectangle.
Euclide raisonnait
essentiellement avec les aires
– v. Méthode d'Euclide
Rectification d'un arc
de courbe: le rendre droit
Méthode de construction pour passer de l'un à l'autre
Possibilité de calculer la longueur.
– a. Rectification: determining the length of an irregular arc segment.
Rectification du cercle: avec règle et
compas, construire un segment ayant la longueur de la circonférence du cercle.
– a. Circle rectification
Rectification uniforme: courbes approchées
par des segments de droites.
– a. Approximation of curves by line segments
Rectification d'un polyèdre: procédé consistant
à le tronquer à partir des milieux de ses arêtes.
– a. Rectification (truncating)
Rectiligne (figure -): ligne polygonale limitée par les lignes droites.
– v. Isothétique

Figure rectilinéaire: rectiligne avec
toutes les lignes voisines à angles droits (Illustration).
C'est une figure dépourvue de trous.
– a. Rectilinear figure
Mouvement rectiligne: mouvement qui
s'effectue le long d'une ligne droite.
– types: mouvement rectiligne uniforme, mouvement rectiligne uniformément
accéléré.
– a. Linear motion or rectilinear motion, uniform acceleration
Récurrence
(démonstration par -) ou démonstration par induction: on démontre que la
propriété, supposée vraie pour n, est aussi vraie pour n+1 et on constate en
outre qu'elle est vraie pour une certaine valeur de n0 (souvent n0
= 1); c'est donc, qu'à partir de cette valeur et par propagation (hérédité),
elle est vraie pour toutes les valeurs de n.
On dit aussi: raisonnement par récurrence.
– v. Démonstration
par récurrence, métaphore
des escaliers
– a. Mathematical induction: a proof technique
Suite ou série récurrente: chaque terme s’exprime à partir du terme qui
le précède ou de plusieurs, comme: Un = Un – 1 + Un
– 2.
– ex. Suite récurrente de Fibonacci: Formule de récurrence des fractales
– a. Recurrence relation: an equation that expresses the nth term of a sequence
as a function of the k preceding terms.
 Récursive: qui se définit en s’utilisant soi-même,
directement ou indirectement.
Récursive: qui se définit en s’utilisant soi-même,
directement ou indirectement.
Idée avec: image dans l'image comme sur cette illustration.
– ex. On peut définir la fonction factorielle de manière récursive: n! = (n –
1)! x n.
– v. Programmation récursive, fractales
– a. Recursion, recursive
Réduction:
contraire
d'agrandissement, zoom-arrière.
Homothétie: toutes les dimensions de la figure sont
multipliées par un facteur k inférieur à
1.
– a. Homothety or homothecy
Réductionnisme: tout peut être
décomposé et analysé en termes de composantes.
– v. Holistique, chaos
– a. Reductionism
Réduire une expression
polynomiale (ou une expression littérale): synonyme de simplifier, mettre ensemble
les termes de même nature.
– ex. x² + 4x + 2 + 5x + 3x² = 4x² + 9x + 4;
(4x – 2)² - (2x + 1)² = 16x² –
16x + 4 – (4x² + 4x + 1) = 12x² – 20x +3
– v. Techniques de base de
l'algèbre, mots usuels du
calcul
– a. Reduction: the rewriting of an expression into a simpler form; To simplify
and collect.
Réduire au même dénominateur: calcul qui conduit
à mettre toutes les fractions compatibles entre elles, prêtes à être
additionnées, car possédant le même dénominateur.
– image: toutes les tartes sont divisées en un même nombre de parts.
–
ex. ![]() au même dénominateur
deviennent:
au même dénominateur
deviennent: ![]()
–
méthode: On multiplie les deux termes de l'une par le dénominateur de l'autre,
ou plus astucieusement par le plus petit commun multiple (PPCM) des
dénominateurs.
– v. Dénominateur,
PPCM
– a. To find, to get a common denominator, a least common denominator
Réduire une figure: la rapetisser; la
reproduire à une échelle inférieure à 1.
Appliquer une homothétie
de rapport k < 1.
– a. Reducing and enlarging a geometric figure
Réduite d'un nombre
irrationnel: fraction irréductible approximant ce nombre.
– ex. Réduites de p: 22/7 ou 355/113.
Les réduites sont obtenues en utilisant un développement partiel de la fraction
continue du nombre irrationnel.
– v. Fractions
continues et réduites / Réduites
des constantes usuelles.
– a. Convergent or nth approximant
Réduite (variable aléatoire -): son espérance
mathématique est nulle et son écart-type
est égal à 1.
– v. Variable aléatoire centrée réduite
– a. Centered variable, standardized variable
Réel (nombre -): tous les nombres que vous
pouvez imaginer: entier, à décimales limitées, à décimales illimitées;
–
notation: ![]() ; privé du zéro
; privé du zéro ![]() ; réels positifs
; réels positifs ![]() ; réels négatifs
; réels négatifs ![]() .
.
–
propriété: ![]()
– v. Nombres réels, tous les types de
nombres
– a. A
real number is a value of a continuous quantity that can represent a distance
along a line
Référentiel: synonyme de repère,
système d'axes.
Notion utilisée surtout en mécanique pour indiquer dans quel monde
(référentiel) on se situe par rapport à un autre.
Référence utilisée pour décrire un mouvement, une trajectoire.
– ex. Le référentiel de l'observateur par rapport au référentiel du train en
mouvement.
– a. Frame of reference
Référentiel en mécanique: association d'un repère d'espace et d'une
échelle de temps.
Réflexion: synonyme de symétrie axiale (miroir).
– a. Reflection
symmetry, mirror symmetry
Réflexive* la propriété s'applique
à lui-même.
– notation: ![]()
– ex. a ³ a est une propriété réflexive car tout a
est égal à a.
a divise a et
réflexive.
a est enfant de a
est antiréflexive.
– v. Symétrique, transitive,
relation d'ordre, vocabulaire
des structures algébriques
– a. Reflexivity, reflective property
Réflexivité* relation
binaire telle que tout élément est en relation avec lui-même.
– a. Reflexive relation
Région: partie du plan
délimité par une frontière.
Région interne et région externe.
– a. Region (in the plane), interior region and exterior region
Règle
(à suivre): proche de méthode à suivre.
Règle de trois ou règle de proportionalité: dans un paquet de 10 bonbons, 3 sont à la
menthe.
Combien de bonbons à la menthe dans un paquet de 20 ?
Réponse: ![]() . On applique la règle de trois, ou du produit en croix.
. On applique la règle de trois, ou du produit en croix.
– v. Pourcentage, rapport, proportion, prorata, fraction,
multiplication
– a. Cross multiplication, "cross your heart"
Règle des signes: avec la
multiplication, deux mêmes signes donnent plus et deux
signes contraires donnent moins.
– ex. 2 × 2 = 4, (–2) (–2) = 4; (–2) × 2 = –4; 2 (–2) = –4
– ex. 3 (5 – 4) = 15 – 12 = 3 et
(–3) (5 – 4) = –15 + 12 = –3
– v. Règle des
signes, multiplication,
distributivité
Règle des priorités: façon de calculer
en suivant les conventions d'écriture des expressions littérales.
– v. Calculs algébriques, priorité des
opérations (PEMDAS …)
– a. Order of
operation, BEMDAS
Règle de Cramer: elle permet de
trouver la solution d'un système d'équations avec autant d'équations que
d'inconnues, valide lorsque le système a une solution unique.
– v. Règle de Cramer
– a. Cramer's rule: an
explicit formula for the solution of a system of linear equations with as many
equations as unknowns.
Règle et compas (construction à
-): construction de figures avec ces seuls instruments, la règle n'étant pas
graduée.
– v. Construction
à la règle et au compas, quadrature
– a. Straightedge
and compass construction, or ruler-and-compass construction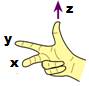
Règle de la main droite: disposition des
doigts servant de moyen mnémotechnique
en physique, notamment en électricité (Illustration).
– v. Règle du tire-bouchon.
– a. Right-hand rule
Réglée (surface -): idée de
construction à la règle.
Surface engendrée par une droite qui se déplace selon la variation d'un
paramètre.
Une surface est réglée si en chacun de ses points on peut faire passer une
droite entièrement contenue dans la surface. Le plan est l'exemple le plus
évident. Le cylindre et le cône en deux autres
exemples.
– ex. Cas du
cylindre, cas de l'hyperboloïde à une nappe.
– v. Génératrice, directrice, surface
développable et surface gauche
– a. Ruled surface, scroll: through every point of S there is a straight line
that lies on S.
Régression
linéaire*: trouver une droite qui représente une série de données, qui approxime
"au mieux" le comportement d'une variable, d'une statistique.
– Synonyme de droite de tendance.
– Calcul: la méthode la plus utilisée est celle des moindres carrés
– a. Linear regression attempts to model the relationship between two variables
by fitting a linear equation to observed data. The most common method for fitting a regression line is the method of
least-squares. Method of least squares.
Régression: en statistiques,
méthode qui permet d'analyser la relation d'une variable par rapport à une ou
plusieurs autres. Elle permet d'approcher une variable inconnue à partir
d'autres mieux connues.
– ex. Les algorithmes d'apprentissage statistique ne prédisent pas l'avenir;
ils se réfèrent à des cas connus du passé pour extrapoler à de nouveaux cas et,
ce à l'aide d'une régression sur les données.
– a. Linear regression
Droite de régression – v. Droite de régression
Régulier ou
simplifiable: Un élément est régulier si on peut simplifier.
– ex. a * c = b * c qui est simplifié en a = b.
– v. Vocabulaire
des structures algébriques
Relatif
(nombre -): nombre avec une signe + ou - .
Nombres entiers relatifs ou abrégés en entiers.
– notation: l'ensemble est noté ![]() .
.
– v. Entier relatif,
types de nombres, absolu, multiplication, règle des signes.
Relation: association d'un
élément d'un ensemble (antécédent) à un élément d'un autre ensemble (image).
Généralisation du concept d'application.
Une relation entre objets mathématiques d'un certain domaine
est une propriété qu'ont, ou non, entre eux certains de ces objets
– notation: ![]() .
.
Relation binaire entre deux
ensembles: un élément est associé à un élément du même ensemble; relation de E vers
E.
– v. Vocabulaire
des structures algébriques
– a. A binary relation associates elements of one set, called the domain, with
elements of another set, called the codomain
Relation d'ordre: relation binaire qui permet de comparer les éléments d'un ensemble entre
eux.
Quatre possibilités exclusives: plus petit, égal; plus grand ou incomparable
(diagramme de Hasse)
– ex. x ![]() y
y
– v. Vocabulaire
des structures algébriques
– a. Partially ordered set or poset
Relation de Bézout*
–
v. Identité de Bézout. et ses développements
Relation de Chasles
–
v. Chasles, Vvecteur, exemple d'application, inégalité
triangulaire
– a. Segment addition postulate.
Relation d'Euler: caractérise les
polyèdres par un invariant.
S + F – A = 2 avec S sommets, F faces et
A arêtes.
– v. Relation
d'Euler
– a. Euler's formula
Relation d'équivalence: fonction qui
définit une sous-famille aux propriétés semblables.
– ex. toutes les droites parallèles à une direction, tous les nombres dont le
reste de la division par 3 est 1.
– propriété: elle est réflexive, symétrique et transitive.
– v. Quotient (ensemble)
– a. Equivalence relation
Les éléments semblables sont
réunis en paquets formant des classes d'équivalence (des paquets d'éléments
semblables).
L'ensemble est constitué de
nouveaux (gros) éléments (les classes).
L'ensemble, ainsi divisé en paquets, est appelé l'ensemble quotient.
Relativité* notion de physique
qui dit que dans un train si vous lâchez une balle, elle tombera à vos pieds
comme cela se passe dans la cour de récréation, comme si la balle ignorait le
mouvement du train.
En fait, tous les objets à bord du train ont "pris" la vitesse du
train et, pour quelqu'un sur le quai, la balle tombe effectivement plus loin
que mes pieds, mais durant la chute mes pieds, eux aussi, ont avancé.
– propriété: Le principe de relativité affirme que les lois physiques
s'expriment de manière identique dans tous les référentiels
inertiels; les lois sont invariantes par
changement de référentiel inertiel.
– v. Relativité.
– a. Principe of relativity
Relativité restreinte** dit que la vitesse de la lumière est une constante (c)
et cette vitesse ne peut pas être dépassée.
Conséquence: les grandeurs comme le temps, la longueur ou la masse varient
selon les vitesses relatives des observateurs.
En outre, il y a équivalence entre matière et énergie via la célèbre formule E
= mc² .
– v. Relativité restreinte.
– a. Special relativity
Relativité générale** l'espace ne peut
être décrit qu'en y incluant le temps.
Un objet massif crée une déformation de cet espace.
L'effet est que tout autre objet massif proche est attiré par lui (image de la
bille qui tourne dans un vase).
La pesanteur est équivalente à une accélération, du
même type que celle que l'on subit dans un ascenseur.
– v. Relativité générale
– a. General relativity
Relèvement ou angle de
relèvement: angle que
fait avec le nord la direction d'un point à terre, d'un bateau, d'un astre, etc.
dans un plan horizontal.
– v. Cap, points cardinaux
– a. Bearing: the horizontal angle between the
direction of an object and another object, or between it and that of true
north.
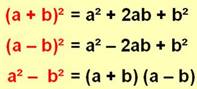 Remarquable (identité -): une formule qui
mérite d'être retenue par cœur; comme les trois indiquées sur l'illustration
Remarquable (identité -): une formule qui
mérite d'être retenue par cœur; comme les trois indiquées sur l'illustration
– v. Identités remarquables
– a. Standard algebraic identities
Rentrant (angle -): angle qui mesure de
180° à 360°.
– v. Saillant, types d'angles
– a. Reflex angle
Repdigit
ou nombre unifome: nombre formé que d'un seul chiffre.
– ex. 22, 555, 7777, 9999999 …
Les repunits ou nombres uniformes en 1 sont composés de 1: 11, 111,1111,
…
– v. Repdigit,
repunit
Repère: axes ayant même
origine permettant de désigner un point dans le plan ou l'espace.
Moyen de repérer les points de l'espace en listant leurs coordonnées.
Un repère est défini par un triplet ![]() , où O est un point du plan et les vecteurs i et j une base du plan vectoriel.
, où O est un point du plan et les vecteurs i et j une base du plan vectoriel.
Il en existe de différentes sortes selon les types d'axes: affine, direct,
log-log, semi-logarithme …
– v. Base et
repère, coordonnée,
référentiel.
– a. Coordinate system
Repère orthogonal: repère dont tous
les axes sont à angle droit, orthogonaux.
Repère orthonormé ou base orthonormé: repère orthogonal
avec la même unité de mesure sur chaque axe, prise comme unité.
– v. Repère
orthogonal et orthonormé
– a. Orthonormal basis
Repère cartésien ou système de
coordonnées cartésiennes: triplet ![]() pour le plan, ou quadruplet
pour le plan, ou quadruplet ![]() pour l'espace, formé d'un point O et d'une base (i, j) ou (i, j, k ) de vecteurs du plan ou de l'espace.
pour l'espace, formé d'un point O et d'une base (i, j) ou (i, j, k ) de vecteurs du plan ou de l'espace.
– v. Cartésien
– a. Cartesian coordinate system
Repère affine: généralisation,
mais souvent synonyme de repère cartésien, notamment dans le cas de 2 ou de 3
dimensions (on dit R2 ou R3).
– v. Cartésien, affine
– a. Affine coordinates
Représentation
(théorie des -)**: branche des mathématiques qui cherche des moyens de
combiner des éléments de base des mathématiques comme les symétries pour créer
des objets plus sophistiqués.
La théorie des représentations est un outil puissant, parce qu'elle réduit des
problèmes d'algèbre abstraite à des problèmes d'algèbre linéaire, un domaine
qui est bien compris.
Cette théorie crée un pont entre la théorie des groupes et l'algèbre linéaire
en attribuant une matrice à chaque élément d'un groupe, selon certaines règles.
Par exemple, l'élément d'identité du groupe sera affecté à la matrice
d'identité.
– v. Mathématiques condensées, nombres
p-adiques, perfectoides, programme
de Langlands
– a. Representation theory
Idée: une représentation
fournit une image simplifiée d'un groupe, tout comme une photo en niveaux de
gris peut servir d'imitation à faible coût de l'image couleur d'origine. En
d'autres termes, il se souvient de
certaines informations de base mais essentielles sur le groupe tout en oubliant
le reste.
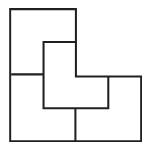
Reptuile: Forme divisible en
plusieurs copies qui lui sont semblables (illustration).
– a. a rep-tile or reptile (confusion possible avec reptile !)
is a shape that can be dissected into smaller copies of the same shape.
Repunit: nombre formé que du
chiffre 1.
– ex. 11, 111,1111, …
Le repunit 11 est un nombre premier. On en
connaît que quatre autres premiers, même si on conjecture
qu'ils sont en nombre infini.
– v. Repunit, repdigit
Réseau:
ensemble
de liaisons.
– ex. Le réseau électrique.
– a. (Bus) network, (electric) grid,
(internet) web
Réseau en combinatoire: synonyme de grille ou
quadrillage de dimension n × n.
– v. Chemins sur réseaux
– a. Grid, lattice path
Réseau en théorie des graphes: graphe connexe
orienté et valué.
– ex. Graphe d'un circuit électrique annoté des intensités sur chaque branche.
– v. Le pont de Königsberg
– a. Network theory: the study of graphs
as a representation of either symmetric relations or asymmetric relations
between discrete objects.
Réseau* en théorie des
nombres: forme de groupe
discret.
Réseau informatique: système de communication entre ordinateurs et
autres machines informatiques.
Le plus simple: deux ordinateurs reliés par un câble.
La liaison peut être un câble (cuivre ou fibre optique) ou les ondes
(Bluetooth, Wifi, téléphone).
Chaque machine est équipée d'une carte réseau (carte électronique) qui émet et
reçoit les données circulant sur le réseau selon son nom caractérisé par une
adresse (adresse IP).
– v. Adresse en décimales pointées (adresse IP), ordinateur (comment ça
marche)
– a. Data communication network (DCN)
Résidu: autre mot pour dire
reste de la division, spécifique du vocabulaire des congruences.
Résidu quadratique: entier a tel qu'il existe un entier x vérifiant ![]()
– v. Résidu quadratique
– a. Quadratic residue: an integer q is called a quadratic residue modulo n if
it is congruent to a perfect square modulo n.
Résidu cubique: idem quadratique
mais avec x3.
–
v. Congruence avec les cubes
– a. Cubic residue
Résolution: en mathématique,
solution d'un problème, d'une équation
Résoudre un problème, une équation, une énigme.
– v. Mots usuels du
calcul, techniques de
base de l'algèbre,
– a. Solving
Résolution des triangles: avec trois mesures
dans un triangle quelconque, trouvez la valeur des trois autres.
– v. Résolution
des triangles
– a. Solving triangles
Résolution ou définition d'une image: en informatique, quantité de pixels par unité de longueur.
– ex: Résolution d'un écran, d'une imprimante, de la souris, etc.
– ex. Un téléviseur
4k a une définition de huit millions de pixels
(3 840 x 2 160 = 8 294 400 pixels).
– a. Pixel density, pixels per inch (ppi), pixels per centimetre (ppcm)
Résolution: en métrologie, capacité à distinguer précisément des détails.
Plus petite variation de la grandeur détectable par l'instrument de mesure.
– ex: Un radar de bonne résolution sera capable de détecter un objet de petite
taille à grande distance ou aussi de distinguer (de discriminer) deux objets
(cibles) proches l'un de l'autre.
– v. Sensibilité, précision
– a. Resolution: smallest change in a quantity being measured that causes a
perceptible change in the corresponding indication.
Résolvante: Équation dérivée de
l'équation à calculer et qui en facilite la résolution.
– v. Équation résolvante
– a. Resolvent formalism
Matrice résolvante, opérateur résolvant**: Dans le cadre d'une
application linéaire, le but est de résoudre un système qui a la même matrice
que le système original, mais on cherche non pas un vecteur solution, mais une
matrice solution.
Resolvent matrix
Résoudre une équation
(résolution d'une équation): trouver les racines de cette équation.
– méthode de base: toute opération effectuée
d'un côté de l'égalité doit être effectuée de l'autre côté (principe de
l'équilibre des plateaux d'une balance).
– v. Équations et en vocabulaire des mathématiques
– a. To solve an equaton, a general rule for solving an equation, equation
solver
Résoudre par combinaison (ou par
élimination): dans un système d'équations, méthode qui consiste à multiplier deux des
équations par deux nombres tels que l'une des inconnues est automatiquement
éliminée.
– v. Système d'équations.
Résoudre par substitution: dans un système
d'équations, méthode qui consiste à exprimer une inconnue en fonction des
autres et, à la remplacer par son expression dans les autres équations.
– v. Système d'équations.
Résoudre un triangle: étant données
trois mesures (longueur des côtés et valeurs des angles) trouver les trois
mesures manquantes.
– v. Résolution des triangles
– a. To solve atrinagle, solving a triangle
Respectivement: veut dire dans
l'ordre indiqué.
– ex. Les moutons A et B sont blanc et noir respectivement veut dire que A est blanc et B est noir.
– a. Respectively
Reste: ce qui reste
lorsqu'un nombre est divisé un nombre entier de fois par une autre, comme la
chute de bois lorsqu'on débite un morceau de bois en mètre.
– ex. 26 / 5 = 5 reste 1.
– v. Division, modulo
– a. Remainder
Résultante (force -): veut dire résultat
de la somme des vecteurs.
– ex. La résultante des forces
de la pesanteur s'applique au centre de gravité d'un
objet.
– a. Net force: the vector sum of forces acting on a particle or object.
Résultat d'une
opération: nombre obtenu après
avoir effectué l'opération.
Plus généralement: ensemble des images d'une opération, d'une transformation.
– v. Somme et
différence, produit,
quotient, loi de
composition interne
– a. Result, output value of an operation; a product is the result of
multiplication,
Retourné (nombre -): nombre dont les chiffres sont écrits dans
l'autre sens, comme 123 et 321.
– v. Retourné
– a. Reversal of a positive integer, digit reversal
Retournement: une figure recto
passe en verso. La pièce pile passe sur face.
Isométrie
du plan qui inverse son orientation.
Plus simplement: une symétrie miroir avec ou non déplacement de l'image.
Retrancher: synonyme de
soustraire, ôter, retirer.
– v. Soustraction
– a. Substraction
Rétrograde (sens -): rotation dans le
sens des aiguilles d'une montre.
Valeur affectée du signe moins.
– v. Direct, orientation
– a. Clockwise (CW)
Rétrograde (transformation -): qui retourne la figure; le recto devient verso.
Synonyme
d'inverse, d'indirecte par opposition à directe.
Transformation
qui inclut une symétrie orthogonale
(une réflexion miroir, une sorte de retournement de la figure).
Les angles orientés sont opposés (signe -) dans la transformation.
Les isométries indirectes sont la réflexion (symétrie axiale) et la réflexion
glissée (réflexion plus translation)..
– v. Transformation directe, symétrie orthogonale, antidéplacement
– a. Reflection and glide reflection are indirect isometries because they do
flip the shape being transformed.
Rétropropagation: en intelligence artificielle,
algorithmes de remontée d'informations qui sert à calibrer (pondérer) un réseau
de neurones durant son "apprentissage".
– a. Backpropagation (BP): algorithm for training feedforward neural networks.
Réunion:
tous
les éléments des ensembles mis en
commun.
Les éléments retenus sont ceux de l'ensemble A ou de l'ensemble B ou …
– notation: ![]() .
.
– ex. réunion ({a, b}, {b, c)}) = {a, b, c}
– v. Opérateur OU
, intersection
– a. Union operator, disjonction
Révolution:
synonyme
de rotation autour d'un objet.
– ex. Une révolution complète de la Terre autour du soleil dure un an.
– a. Rotation refers to an object's spinning motion about its own axis.
Revolution refers the
object's orbital motion around another object.
Révolution (surface de -): engendrée par une
droite (directrice) en suivant une courbe (génératrice) parallèlement à une
droite (axe de révolution).
Une surface de ![]() .
.
– v. Cas
du cylindre
– a. Surface of revolution, generatrix (rotating curve), axis of rotation
Rhind
(papyrus -): écrit par le scribe Ahmès, il contient 87 problèmes d'algèbre, de
géométrie et d'arpentage avec les solutions. Usage des fractions égyptiennes.
– Histoire des
mathématiques
Rhombe: vieux nom pour losange.
Cette figure était associée aux louanges (losange en vieux français) sur les
armoiries féodales.
– étym. En latin rhombus est le
losange.
– a. La langue anglaise a conservé ce mot: rhombus, rhombohedron …
Rhombique: qui a la forme
d'un losange.
Rhomboèdre: parallélépipède dont
les six faces sont des losanges.
– v. Rhomboèdre
– a. Rhombohedron
Rhomboïde: quadrilatère en
forme de cerf-volant, qui admet pour axe de symétrie l'une de ses diagonales.
– a. Attention rhomboid en anglais désigne le parallélogramme dont les côtés
adjacents sont inégaux et sans angles droits.
RHS: Right hand side, la
partie droite d'une équation par exemple; LHS: left hand side.
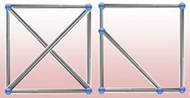
Rigide (polygone ou
graphe -): qui comporte des éléments qui rendent la forme géométrique indéformable (Illustration).
– proches: indéformable; déformable, flexible
– v. Polygone ou graphe rigide
– a. Rigid polygon or graph: distance-preserving. A graph that is not rigid is
said to be flexible
Romains
(chiffres -) ou numération romaine: I, II, III, IV, VI, VII, VIII, IX, X …
– v. Chiffres romains
– a. Roman numerals
 Rond (nombre -): nombre entier ou ramené à un entier par
arrondi.
Rond (nombre -): nombre entier ou ramené à un entier par
arrondi.
– v. Arrondi
– a. Round number
Nombre ronds (de Hardy): dont les facteurs sont très petits par rapport
au nombre.
si les facteurs sont inférieurs à racine carrée de n, il est "square-root
smooth".
– ex. 324 = 22 ٠34
– v. Nombres ronds ou à petits facteurs
– a. Round Number: a number that is the product of a considerable number of
comparatively small factors.
Rosace, rose, rhodonea:
famille
de courbes en r = sin (k.A).
– propriété notable: l'aire des pétales est égale à 50% ou 25 % du disque qui
les contient selon que k est pair ou impair.
– a.
Shape of a rose, rose, rhodonea curve
Rosette: terme réservé aux rosaces avec pétales qui se chevauchent.
En architecture et décoration, motif montrant les pétales vus du dessus
– a. Rosette
Rotation: transformation par
glissement d'une figure en la faisant pivoter dans un plan.
Par rotation, un point M est transformé en un point M' tel que MM' est un arc
de cercle de centre O, le
centre de la rotation, et d'angle ![]() , l'angle de la
rotation.
, l'angle de la
rotation.
Une symétrie
centrale est une rotation d'angle 180°.
– v. Transformations
Ne pas confondre rotation et
révolution
Rotation: un objet tourne sur lui-même;
Révolution: il tourne autour d'un autre objet.
– a. Rotation refers to an object's
spinning motion about its own axis.
Revolution refers the object's orbital motion around another object.
Mécanique: Un objet 2 est en rotation par rapport à un objet 1 si et seulement si il existe à chaque
instant une droite de l'objet 2 immobile par rapport à l'objet 1.
Rotosymétrique*: Un polygone est
dit rotosymétrique d'ordre n ou plus brièvement n-rotosymétrique quand il
présente un axe de rotation d'ordre n.
Roto-réflexion ou anti-réflexion**: une sorte
d'antidéplacement (isométrie qui renverse l'orientation) de l'espace euclidien
de dimension 3.
– a. Improper rotation or rotoreflection
Roto-inversion **: composée d'une
rotation autour d'un axe et d'une inversion par rapport à un point de cet axe.
Roue
(crible de la -): critère de primalité, alternative au crible d'Ératosthène.
Méthode qui s'appuie sur la connaissance des k plus petits nombres premiers et
évite l'analyse d'une grande quantité de nombres composés.
– v. Crible de la roue
– a. Wheel factorization is an improvement of the trial division method for
integer factorization.
Roulette: synonyme de cycloïde et autres courbes en -oïdes.
Une généralisation des cycloïdes, épicycloïdes, hypocycloïdes, trochoïdes, et
courbes développantes.
Courbe décrite par un point (générateur ou pôle) d'une courbe
qui roule sans glisser le long d'une autre courbe immobile.
– a. Roulette
Roulis: mouvement de
va-et-vient latéral d'un véhicule (navire, avion).
En regardant vers l'avant, le roulis est un balancement sur la droite puis la
gauche, etc.
– v. Les six degrés de liberté.
– a. Pitch, roll and yaw (tangage, roulis et
lacet).
Route: angle entre la
direction suivie par le véhicule (avion, bateau, …) et la direction du nord
– v. Cap
– a. Course
La route est égale au cap en l'absence de dérive. La dérive est due aux
courants ou aux vents. Dans le cas général, la route est égale au cap plus la
dérive: R = G + D.
RSA: méthode de cryptage qui n'hésite pas à laisser sa clé connue de
tous (clé publique), car le décodage est basé sur la factorisation
quasi-impossible de très grands nombres.
Le nom vient des initiales des inventeurs: Rivest, Shamir et Adleman;
– v. Cryptage ou chiffrement RSA.
– a. RSA (Rivest–Shamir–Adleman) is a public-key cryptosystem.
Ruban de Moebius: ruban collé pour
former une boucle, avec une extrémité retournée avant le collage.
Présente une seule surface, ce qui est extraordinaire.
La bouteille de Klein
est encore plus curieuse puisque, en plus, elle n'a même pas de bord.
– v. Moebius.
– a. Mobius strip
Rubik's cube ou cube de
Rubik: cube formé de
petits cubes articulés de couleurs, inventé en 1974 par Ernö Rubik, un
hongrois.
L'objet du puzzle consiste à redonner sa couleur à chaque face en faisant
pivoter une face de 9 cubes à la fois.
Une fois connus les principes, sa résolution demande de la patience mais n'est
pas très compliquée. Le résoudre en un temps record devient alors le défi.
L'algorithme théorique le plus court pour terminer le Rubik's cube est
baptisé algorithme de dieu.
3x3x3: forme la plus connue du cube
d'Erno-Rubik. Aussi connu sous le nom de cube hongrois, il se compose de 6
faces, composées elles-mêmes de 9 facettes de couleurs
2x2x2: ou pocket-cube ayant des rangées de 2 facettes en hauteur,
largeur et profondeur
Il existe aussi des 4x4x4 (revenge), 5x5x5 (professor) et 6x6x6 (beast).
–
v. Rubik
– a. Rubik's cube
![]()
|
Voir |
|
|
Aussi |
|
|
Autres |
|
|
Cette page |


