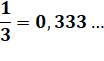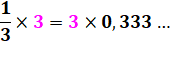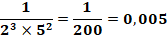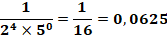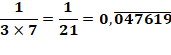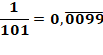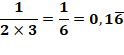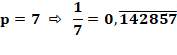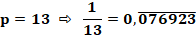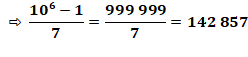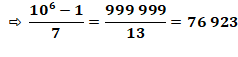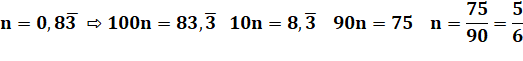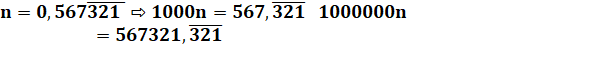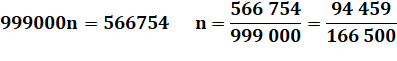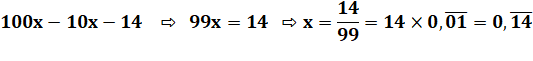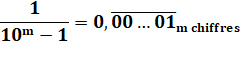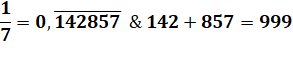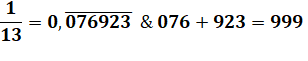|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
Humour
D'après un cartoon de
JIJI-Maths
Voir Pensées et Humour
|
NOMBRES PÉRIODIQUES Développement
décimal périodique Conversion d'un nombre décimal en fraction Nombre
à décimales ayant une tranche de décimales
qui se répètent. Ex: 78/17 = 4,5882352941176470 5882352941176470 5882352941176470 … Le
bloc de chiffres répété est appelé période
ou tranche récurrente (anglais: repetend).
Théorème Tout quotient
de deux entiers possède une écriture décimale finie ou
périodique. La
partie périodique peut être précédée d'un certain nombre de décimales. La fraction formée de deux
entiers est un nombre rationnel. |
Voir Cartographie
des nombres périodiques
Voir Développement décimal d'un nombre / Nombres à
permutations circulaires
Le saviez-vous
|
|
C'est
juste! Multiplions
maintenant par 3: |
|
Voir Nombres
rationnels et 0,999…
Formule express: calcul de la fraction (F)
égale au nombre périodique (D)

Voir Explications
Merci à Landri Gallaz pour
ses suggestions
![]()
|
|
|||
|
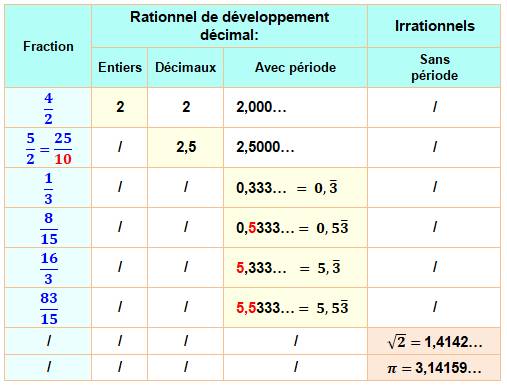
Un nombre rationnel peut s'exprimer sous la forme d'une
fraction, qui est, en fait, la division de deux nombres entiers. L'ensemble
des nombres rationnels est noté: Le développement décimal d'un
nombre rationnel (lorsqu'on effectue la division) peut prendre plusieurs
formes: entier, décimal ou avec période. |
|
||
|
Nombre entier |
Si la
division "tombe" juste. Aucun chiffre derrière la virgule. |
||
|
Nombre décimal |
Si le développement est limité. Exemples 5/2
= 25/10 = 2,5 = 2,5000… 123,456
= 123456/1000 = 123,456000… (= 15432 / 125 en simplifiant). |
||
|
Nombre avec période |
Si le
développement présente une suite de chiffres qui se répètent sans fin
Exemples Nombre
périodique avec période à un chiffre: 1/3 = 0.333… (3 est la période) Nombre
périodique avec période à plusieurs chiffres: 1/7 = 0,.142857142857… Nombre
périodique avec partie fixe décimale: 8/15 = 0.5333… Nombre
périodique avec partie fixe entière: 16/3 = 5,333… Nombre
périodique avec partie fixe entière et partie fixe décimale: 83/15 = 5,5333… Bouquet
final: 864 193 / 7 000 = 123,456 142857 142857 … |
||
|
Nombre irrationnel |
Nombre à
virgule, comportant une infinité de chiffres sans répétition >>> |
||
Merci à Laurine M. pour son questionnement
|
|
||
|
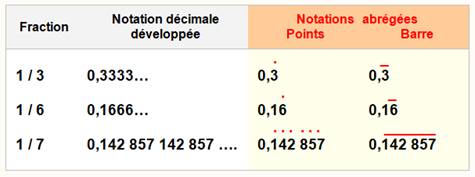
Notations classiques Pour
matérialiser sans ambiguïté les chiffres qui se répètent, les décimales récurrentes, on les surmonte d'un
point sur chacun ou d'une barre sur le bloc de chiffres répétés. |
Exemples
Plus rarement,
les décimales récurrentes sont mises entre parenthèses ou entre crochets. La barre
horizontale de surlignement s'appelle vinculum. |
|
|
Notation anglo-saxonne |
En anglais, la virgule devient un point et le zéro
initial est omis.
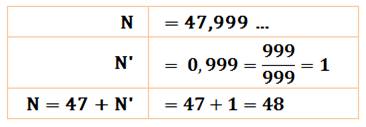
Bel
exemple d'emploi de cette notation dans la résolution du célèbre puzzle du quatre-quatre. Elle
permet d'obtenir le 9 avec seulement deux 4 de la manière suivante:
|
|
|
Notation indienne |
On trouve
parfois un "i" à la fin de la période. 1/7 = 0,142857 i Attention
à la confusion possible avec les nombres
complexes |
|
|
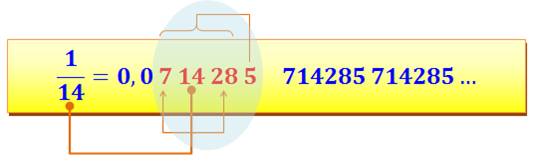
La fraction 1 / 14
présente une bien étrange curiosité.
|
|
|
||
|
Tout
nombre rationnel (n = p/q) a un développement décimal périodique
(éventuellement formé de 0 répétés). La
réciproque est vraie: un nombre périodique peut toujours être mis sous forme
rationnelle (une fraction). Every rational number has
a periodic (or terminating) decimal expansion. The converse is also true; a
periodic expansion always represents a rational number. |
Autre formulation Soit n un
nombre réel,
|
|
|
|
|||
|
Théorème du développement
périodique: Soit n un
nombre entier tel que n > 1 et PGCD (10, n) = 1, et soit a un autre nombre entier avec a Autrement dit: une fraction dont le numérateur est plus petit que le dénominateur et
dont le dénominateur n'est ni divisible par 2 ni par 5 a un développement
décimal périodique. Les trois cas possibles |
|||
|
Développement
décimal avec quantité de chiffres fixe si: |
n est terminé par un zéro. n divisible par 2 et par 5. |
|
|
|
Développement
décimal périodique pur (sans partie fixe) si: |
n divisible ni par 2 et ni par 5 |
|
|
|
Peu
comporter une partie fixe si: |
n est divisible par 2 ou par 5 |
|
|
Anglais:
periodic decimal expansion
|
Nombres périodiques |
|
|
|
Soit p un
nombre premier (hors 2 et 5):
|
|
|
|
Si L est
la longueur de la période, alors p divise 10L – 1; Le motif
de la période est M = (10L
– 1) / p = (99…9) / p. |
|
|
|
Petit théorème de Fermat (1640) ap – 1 avec p premier ne divisant
pas a. Voir Ce
théorème |
Application à notre cas Pour p premier, p divise 10p – 1 – 1. |
|
|
Amusements Le p-ième
chiffre de 1/p est le premier chiffre de la période. Le
précédent résulte de la division de 9 par l'unité de p. |
7éme
chiffre de 1/7 = 1 13éme chiffre de 1/13 = 0 6éme
chiffre de 1/7 = 7 car 7 x 7 = 49 12éme chiffre de 1/13 = 3 car 3 x 3 = 9 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
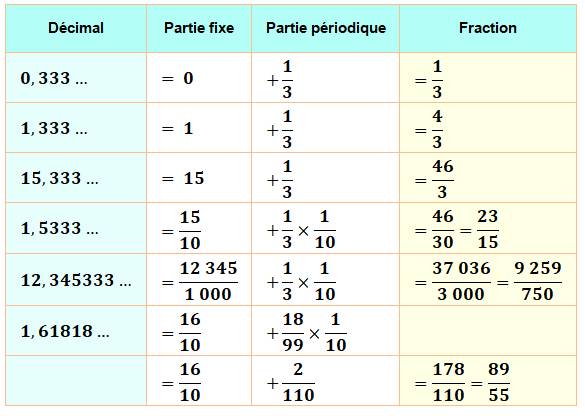
Période pure Nous
allons donner des exemples qui illustreront la procédure de conversion. 0,3333… Nombre cyclique de période 1
0,1212… Nombre cyclique de période 2
0,51212… Nombre cyclique de période 2 avec partie fixe
Autres exemples
|
||||||||||||||||||||||||||||||||||||||||
Voir Nombres rationnels / Nombres cycliques et sommes infinies /
Fraction pour approximer un irrationnel
/ Nombres en N/999…
Nombre 1,61818…
(Approximation du nombre d'or)
Site: Calculateur decimal/ fraction –
Calculis
|
|
|||
|
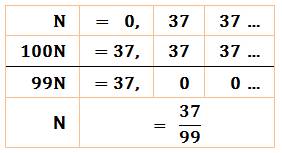
Comment
transformer un nombre périodique simple en
fraction? Multiplions
par 10Période = 102 Et faisons la
différence. Le cas échéant,
la fraction est réduite. |
|
||
|
Bilan |
La
fraction correspondant à un nombre périodique de période P, de longueur p,
est la fraction ayant pour numérateur P et pour dénominateur un 9-repdigit de longueur p. |
||
|
Comment
transformer un nombre périodique mixte en
fraction? Multiplions
par 10Longueur mixte = 102 Puis
multiplions par 10Période = 103 Et
différence des deux. |
|
||
|
Bilan |
La
fraction correspondant à un nombre périodique de période P, de longueur p,
avec partie mixte M de longueur m est la fraction ayant pour numérateur (MP –
M) et pour dénominateur un nombre de p fois 9 suivi de m zéros. |
||
|
Comment
transformer un nombre périodique avec partie
entière en fraction? On
calcule la fraction en ignorant la partie entière puis on ajoute la partie
entière. |
|
||
|
Bilan |
En
présence d'une partie entière, celle-ci est ajoutée à la fraction trouvée
pour la partie décimale. |
||
|
En
présence d'une période composée de 9? |
|
||
|
Bilan |
Validation
de l'écriture
courante des nombres en xxx,999 = xxx+1. |
||
Voir Justification
avec progression géométrique / Repunits
et nombres périodiques / Brève
812
|
|
|||
|
|
|||
|
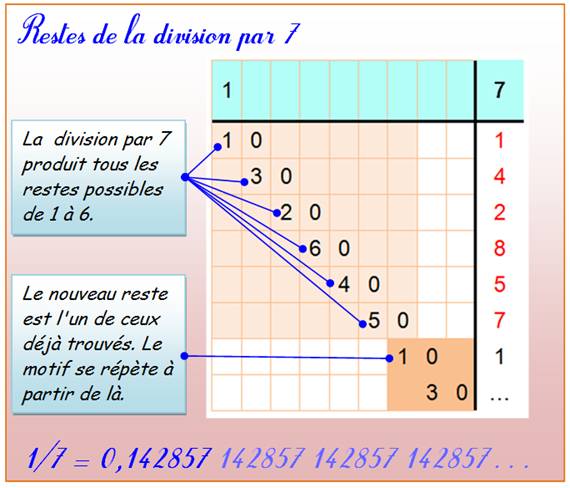
Les
chiffres de la période (division
euclidienne) Exemple 1/7 =
0,142857 …10 = 0,1111 …8 = 0,125125 …9 |
En base 10 10 = 1 x 7 + 3 3 x 10 = 4 x 7 + 2 2 x 10 = 2 x 7 + 6 6 x 10 = 8 x 7 + 4 4 x 10 = 5 x 7 + 5 5 x 10 = 7 x 7 + 1 1 x 10 = 1 x 7 + 3 etc. |
En base 8 8 = 1 x 7 + 1 1 x 8 = 1 x 7 + 1 1 x 8 = 1 x 7 + 1 etc. En base 9 9 = 1 x 7 + 2 2 x 9 = 2 x 7 + 4 4 x 9 = 5 x 7 + 1 1 x 9 = 1 x 7 + 2 etc. |
|
|
La longueur de la période L est déterminée par
la plus petite valeur telle que:
D'une
manière générale: |
Pour p = 7
La période est de 6 chiffres |
||
Voir Division par 9 / Division
posée / Base
de numération / Conversion
des nombres en base b – Programme / Nombre
142 857
Produit
de périodes

|
|
||
|
Le
développement décimal d'une fraction périodique de période paire avec
dénominateur premier, hors 2 et 5 est tel que la première moitié est le complément
à 9 de la seconde moitié. |
Exemples
|
|
|
|
||
|
Lorsqu'une fraction ne peut pas être convertie en nombre décimal, elle est périodique. |
|
|
|
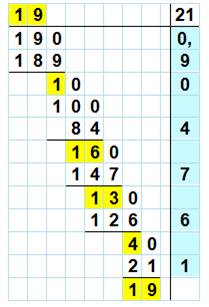
La
démonstration repose sur le fait que les restes sont compris entre 1 et 20 (en jaune sur l'exemple) et qu'à un
moment donné on retrouve la même quantité à diviser. La
succession des chiffres du quotient peut être plus ou moins longue entre 1 et
20 chiffres. |
|
|
|
|
|
|
Deux types
de nombres premiers selon leur période:
Voir Trouver
quand le premier est long ou pas Par exemple,
les nombres suivants possèdent la périodicité maximale possible. Ce sont les
nombres premiers longs.
n
= 17 p = 16 r = 0588235294 117647 n
= 19 p = 18 r = 0526315789 47368421 n
= 23 p = 22 r = 0434782608 6956521739 13 n
= 29 p = 28 r = 3448275862 0689655172 4137931 n
= 47 p = 46 r = 0212765957 4468085106 3829787234
0425531914 893617 n
= 59 p = 58 r = 1694915254 2372881355 9322033898
3050847457 6271186440 67796610 n
= 61 p = 60 r = 1639344262 2950819672 1311475409
8360655737 7049180327 8688524590 n
= 97 p = 96 r = 1030927835 0515463917 5257731958
7628865979 3814432989 6907216494 8453608247 4226804123 7113402061 855670 Conjecture Ces nombres
premiers particuliers, dits premiers
longs, sont en nombre infini et leur densité tend vers la constante
d'Artin. C = 0,373
955 813 6… |
|
Voir Conjecture / Nombre
0, 373… / Division védique
![]()
|
|
||
|
|
= 0,12345679 0123456790 … |
|
|
|
= 0,98765432 0987… |
|
|
|
= 0,123456789
0123456789 01234 ... |
|
|
|
= 0,123456789
123456789 1234 ... |
|
|
|
= 0,987654321
0987654321 … |
|
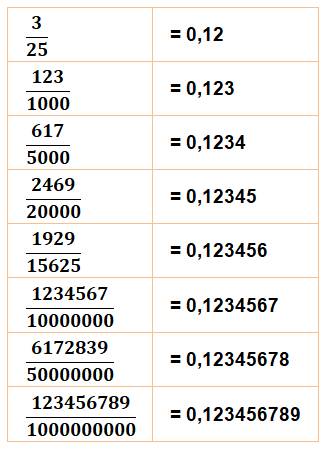
Pour
information – Nombres décimaux pannumériques
|
|
|
|
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()
Renvois de liens
>>> Nombre de cycles et leur
longueur
>>> Liste des valeurs
périodiques pour n < 100
>>> Nombres premiers longs
>>> Bilan
>>> 1/53 - exemple de 4e
catégorie
>>> Nombre périodique et
puissance de 2