Orientation Glossaire	Atlas / Usage des Nombres / Outils / Fondements / Théorèmes
Débutant DicoMot DicoNombre	CONJECTURES

Définition	Affirmation d'une loi que l'on pense être vraie, parce que largement vérifiée, sans exemple contraire, mais non démontrée. - Hypothèse formulée sur un énoncé dont on ne connaît pas la démonstration. - Problème non résolu.
Origine	Latin conjectura: conjecture (aussi: interprétation des songes). Conjectura mentis divinae: conjecture sur la pensée divine.
Expression	Se perdre en conjectures Se livre à des conjectures Ne pas confondre avec conjoncture

Anglais	Conjecture: Unsolved problem. Guess, assumption, inference and speculation.
En savoir plus	Démonstration Principales conjectures 23 problèmes de Hilbert 7 problèmes de la fondation Clay Autres problèmes ouverts Cinq conjectures citées dans le roman 676 Crises en maths
Cette page	http://villemin.gerard.free.fr/Referenc/Vocabula/GlosC/Conjectu.htm

Un peu d'anglais

A wealth of numerical evidence supports the conjecture, but so far a proof has eluded mathematicians.

La conjecture est attestée par une abondance de preuves numériques, mais à ce jour la preuve échappe aux mathématiciens.

Voir Anglais

Principales conjectures résolues (validées ou infirmées)

Voir	Nom - Auteur	Domaine	Origine	Qui	État	Fin
>>>	C. d Kepler	Empilement des sphères	1611	Kepler	Hales	2014
>>>	C. de Catalan	Nombres consécutifs et puissances.	1844	Catalan	Mihailescu	2002
>>>	C. de Bertrand	Nombre premiers entre n et 2n	1845	Bertrand	Tchebychev	1852
>>>	C. de Géométrisation	Classification des géométries.	1970	Thurston	Perelman (?)	2002
>>>	C. de Langlands	Théorie des nombres et de la représentation des groupes.			Lafforgue (?)	2002
>>>	C. de Poincaré	Sphère et espace tridimensionnel.	1904	Poincaré	Perelman	2002
>>>	C. de Fermat	Somme de puissances.	1637	Fermat	Wiles	1995
>>>	C. STW Shimura- Taniyama - Weil	Courbe elliptique et formes modulaires.	1968	STW	Wiles (partiel)	1995
>>>	Nb. de Carmichael	Il y en a une infinité.	1910	Carmichael	Alfort	1994
>>>	C. de Mordell	Quantité finie de solutions pour les surfaces diophantiennes à trou.	1922	Mordell	Falting	1984
	C. de Merten				Contre exemple	1983
>>>	C. des constellations de premiers	Quantité probable de constellations			Hardy et Littlewood
>>>	C. des Quatre couleurs	Coloriage des cartes.	1879	Cayley	Résolue	1976
	C. du pavage périodique	Tout pavage du plan peut se ramener à un pavage périodique.			Penrose - Fausse	1974
>>>	C. d'Euler	Somme de puissances		Euler	Contre exemple	1966
>>>	C. de Cantor	Hypothèse du continu.	1878	Cantor	Cohen - indécidabilité	1963
	C. de Ramanujan	x^2 + 7 = 2^n n'est possible que pour n = 3, 4, 5, 7 ou 15.	1911	Ramanujan	Trygve	1960
>>>	C. d'Euler	Carré gréco-latin.	17..	Euler	Bose …	1959
>>>	C. Polya	Quantité de facteurs	1919	Polya	Haselgrove	1958
	C. d'Erdös	"Erdős discrepancy problem"	1932	Erdös	Terence Tao	2015
	C. d'Erdös	Propriété des triangles: théorème d'Erdös-Mordell.	1935	Erdös	Mordell	1937
>>>	C.Duffin-Schaeffer	Approximation des réels par des fractions	1941	Duffin et Schaeffer	Dimitris Koukoulopoulos James Maynard	2019
>>>	Nb. de Fermat	Ils sont tous premiers.	1650	Fermat	Contre exemple
>>>	C. de corrélation gaussienne	Inégalité gaussienne	1955		Thomas Roven
>>>	C. de Fermat (et Pascal)	Tout nombre entier est la somme d'au plus trois nombres triangulaires.			Gauss
>>>	A. Gelfondr	La somme des chiffres d'un nombre premier a autant de chance d'être paire qu'impaire.	1968	Mauduit Rivat	Résolue	2010
>>>	Cartes	Trois couleurs suffisent si …	1976	Steinberg	Infirmée	2016
>>>	Courbure	Conjecture de la courbure L2 (relativité)	2000	Sergiu Klainerman	Sergiu Klainerman, Igor Rodnianski et Jérémie Szeftel	2016
>>>	Courbes	Conjecture du rectangle inscrit dans une courbe fermée	1911	Toeplitz	Joshua Greene et Andrew Lobb	2020

Principales conjectures ouvertes

>>>	C. ABC	Facteurs identiques dans A + B = C	1985	Oesterlé et Masser
>>>	C. d'Andrica	2cart maximum entre premiers
>>>	C. d'Artin	Nombres premiers et période maximale		Andrica
>>>	C de Bateman-Horn	Nombres premiers jumeaux et leur répartition	1962
>>>	C. de BSD Birch Swinnerton-Dyer	Équations diophantiennes - courbes elliptiques de genre Un - et leurs solutions
	C. de Fermat-Catalan	x^p + y^q = z^r avec 1/p+1/q+1/r <1 a un nombre limité de solutions		Fermat-Catalan
>>>	C. de Catalan-Dickson	Toute suite aliquote de termine en boucle ou par 1.
>>>	C. de Dyson	Aucun retourné d'une puissance de 2 n'est une puissance de 5.
>>>	C. Erdös-Szekeres	Quantité minimale de points pour obtenir à coup sûr un polygone convexe donné.
	C. Inverse de Galois	Tout groupe fini est le groupe de Galois d'une extension galoisienne des nombres rationnels. Hamet Seydi, sénégalais, élève de Grothendieck, aurait démontré ve qui deviendrait le théorème inverse de Galois.
>>>	C. de Gilbreath	Séquence sur la différence entre nombres premiers successifs
>>>	C. de Goldbach	Tout nombre pair est somme de deux nombres premiers.	1742	Goldbach
>>>	Conjecture F	Polynôme ax² + bx +c et génération de nombre premiers	1923	Hardy et Littlewood
	C. de Hodge	Géométrie complexe à partir de briques simples (Cohomologie)
>>>	C. de Landau-Siegel	Répartition des nombres premiers jumeaux	1936	Landau Siegel
>>>	C. de Legendre	Il existe toujours un nombre premier entre deux carrés successifs. Ex: 10² < 107 <11² < 131 < 12²
>>>	C. de Palis	En théorie du chaos, des phénomènes divergents s'accumulent vers le même attracteur.	1990	Palis
>>>	C. de Polignac	Infinité de premiers jumeaux, cousins, sexy …	1849	Polignac
>>>	C. de Riemann	Répartition des nombres premiers On la nomme hypothèse de Riemann pour signifier que l'on se situe au-delà de la simple "devinette" mathématique.	1859	Riemann
	C. de Schannel	Nombres transcendants
>>>	C. de Sierpinski	5/n = 1/a + 1/b + 1/c a toujours une solution		Sierpinski
>>>	C. de Syracuse (ou Collatz)	Le cycle 3n + 1 retombe toujours à 1.	1937	Collatz
>>>	C. de Turing et Church	Un problème ne pouvant être résolu par une machine de Turing ne peut l'être par l'esprit humain.		Turing et Church
>>>	C. d'Erdös-Straus	4/n = 1/a + 1/b + 1/c a toujours une solution		Erdös et Straus
	C. des 4 exponentielles	Parmi e^a.c, e^a.d, e^b.c, e^b.d , l'une est transcendante …
	Éq. de Navier-Stokes	Équations de la mécanique des fluides, turbulence
>>>	Nb. de Carmichael	Indicateur d'Euler 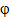(n) = 1 et ses solutions		Carmichaël
>>>	Nb. Parfait impair	Il n'en existe pas, mais ce n'est pas démontré.
	Nombres carrés plus 1	Il existe une infinité de nombres premier égal à un carré incrémenté de un
>>>	Nb. de Fermat	Il a une infinité de premiers de Fermat	1844	Eisenstein
>>>	Nb. premiers jumeaux	Il y en a une infinité
>>>	Rep-units	Il y en a une infinité
>>>	Pb. P / NP	Problème à combinaisons foisonnantes (cas du voyageur de commerce)