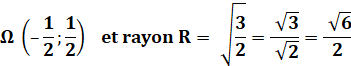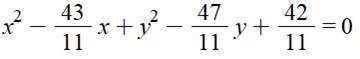NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/12/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	Propriétés				Glossaire Géométrie
INDEX Cercle Géométrie	Cercle	Propriétés	Équations	Théorèmes
	Programmation*	Fondements	Angles	Partage
			Tangente
		Sommaire de cette page >>> Équations du cercle >>> Trouver le rayon et le centre >>> Équation du cercle passant par trois points

* Programme Scratch

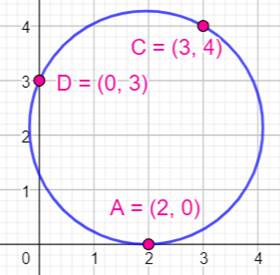
Équation du cercle

Tout point de la circonférence est à la distance R (rayon) du centre. De sorte que pour tout point M: x² + y² = r² (théorème de Pythagore)

Voir Centre du cercle / Construction du centre

ÉQUATIONS du CERCLE
Coordonnées cartésiennes Cercle de centre O (0, 0)	x² + y² = R²
Cercle de centre I (a, b)	(x – a)² + (y – b)² = R²
Coordonnées polaires	x = a + R cos y = b + R sin
Coordonnées paramétriques	x = a + R (1 – t²) / (1 + t²) y = b + 2Rt / (1 + t²) avec t = tg()
Avec diamètre AB (x1, y1, x2, y2)	(x – x1)(x – x2) + (y – y1)(y – y2) = 0

Voir Application à l'ennéagone et sa construction

Trouver le rayon et le centre
Équation	x² + y² + x – y – 1 = 0
Méthode	Mettre sous la forme d'une somme de deux carrés, l'un en x et l'autre en y.
Carré en x (Général)	x² + 2ax + a² = (x + a)²
Départ de carré en x (Ici)	x² + x
Égalité en x	2ax = x a = 1/2
Pour les x
Carré en y (Général)	y² + 2ay + a² = (y + a)²
Départ de carré en y (Ici)	y² – y
Égalité en y	2ay = –y a = –1/2
Pour les y
Retour à l'équation qui devient	x² + x + y² – y – 1 = 0
Forme finale
Paramètres du cercle

Voir Forme complexe / Suite pour le cercle passant par deux points quelconques

Équation du cercle par trois points – TROIS méthodes

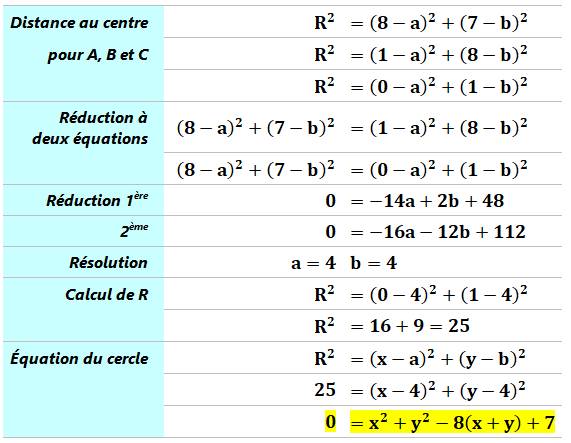
Distance au centre	Trois équations témoignant que chacun est à la même distance du centre du cercle.	>>>
Triangles rectangles inscrits	Trois équations témoignant que chacun est à la même distance du centre du cercle.	>>>
Médiatrices	Équations des deux médiatrices des segments joignant les trois points deux à deux.	>>>

Cercle par trois points – Avec centre		haut
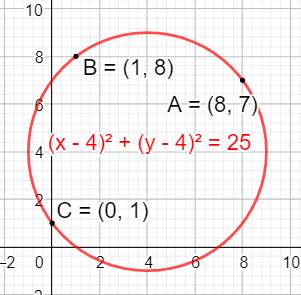
Problème Trouver l'équation du cercle passant par les trois points A, B et C. Idée Utiliser le fait que ces trois points sont à la même distance du centre du cercle dont les coordonnées inconnues sont a et b. Calculs On calcule les coordonnées a et b du centre du cercle, et on les injecte dans l'équation générique du cercle.

Équation avec triangles rectangles inscrits		haut
Problème Trouver l'équation du cercle passant par les trois points indiqués sur la figure. Idée Tracer les perpendiculaires à AD et CD en A et C. Elles se coupent en B. Les triangles rectangles ABD et BCD sont inscrits dans le cercle, alors BD est un diamètre du cercle. Étapes Trouver les équations des droites AD et CD. Trouver les équations des perpendiculaires. Leur pente est m' = –1/m, avec m la pente de la droite à laquelle elle est perpendiculaire. Elle passe par le point A ou C avec dans ces cas y = m'x + b ce qui permet de calculer b. Calculer les coordonnées du point d'intersection D: solution commune en x et y pour les deux perpendiculaires. Trouver l'équation du cercle dont le diamètre est BD (rappel: les angles sont droits en A et en C et BD est un diamètre). 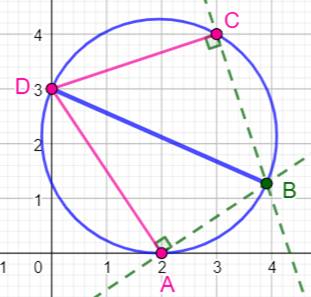Calculs En développant	Cercle passant par trois points Tracé des perpendiculaires et du diamètre BD Les triangles rectangles ABD et BCD sont inscrits dans le même cercle qui n'est autre que le cercle passant par A, C et D. 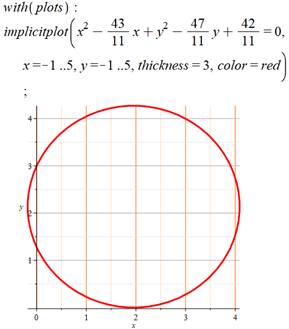Le point B est bien situé sur le cercle et Bd est un des diamètres. Vérification avec Maple

Voir Cercle et trois points

Suite	Arc de cercle – Coordonnées du point milieu Calcul de l'aire du cercle par intégrale Cercle d'Apollonius Théorèmes Cercle unité et triplets de Pythagore Programmation du dessin du cercle – Classique ou récursive Programmation du dessin du cercle avec Scratch
Voir	Cercle – Index Géométrie – Index
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/Equation.htm