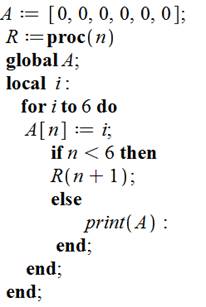Programmation récursivité

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/03/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Informatique
Débutants Programmation	Programmation				Glossaire Général
INDEX Programmation Informatique	Procédure	Palindrome	Récursivité	Redondance
		Sommaire de cette page >>> Induction et récursivité >>> Récursivité et factorielles >>> Récursivité et permutations >>> Programmation permutation avec "permute"

Récursivité

Comme les boucles d'oreilles de la Vache qui rit ou encore les fractales et leur autosimilarité, la récursivité est une invention diabolique qui se renvoie à elle-même.

Certains langages de programmation sont bien connus pour posséder ces propriétés: LISP ou PROLOG. Mais, il est possible d'implémenter des procédures récursives avec tout langage de programmation.

Exemple de définition récursive (qui utilise sa propre définition pour se définir)

Un nombre est polydivisible s'il est divisible par sa quantité de chiffres et si ce nombre tronqué de son unité est aussi polydivisible. >>>

Récursif

Récurrent: qui se répète, qui revient régulièrement

Du latin recurrens: revenant rapidement en arrière; de recurro: revenir en courant.

Maths: suite ou série récurrente: chaque terme s’exprime à partir du terme qui le précède. U_n = U_{n – 1}+ U_{n – 2}. Suite récurrente de Fibonacci.

Récursif: qui se définit en s’utilisant soi-même, directement ou indirectement. On peut définir la fonction factorielle de manière récursive: n! = (n – 1)! x n

Naturam expellas furca, tamen usque recurret: tu peux chasser le naturel à coups de fourche, il reviendra toujours au galop.

Induction et Récursivité
La démonstration par induction part du principe que si l'on sait une étape (départ) et que l'on sait passer d'une étape à la suivante (récurrence), alors on sait faire toutes les étapes.	Un algorithme récursif part du principe qu'ayant défini une procédure (une recette, une méthode) pour passer d'une étape à la suivante, il suffit de définir le départ et d'appliquer la dite procédure de manière répétitive.
Magie pour atteindre une démonstration sans explorer tous les cas	Magie pour atteindre un résultat, sans détailler toutes les étapes de calcul
Exemple avec la somme des entiers jusqu'à n: Je sais que si S_n = ½ n (n + 1) alors S_n+1 = ½ (n+1) (n + 2) et que cette formule est vraie pour n = 2 (en effet: ½ x2 x 3 = 3 et S est bien égal à 1 + 2 = 3.	Exemple avec le tracé du cercle Procédure cercle: avancer d'un pas et tourner à gauche d'un cran. Programme cercle: Procédure cercle tant que le point courant est différent du point de départ.

Récursivité & factorielles
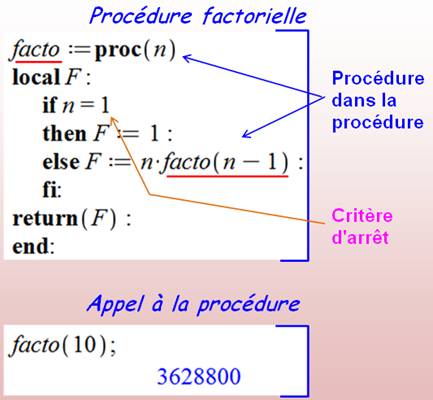
Méthode itérative (classique) F est mis à 1 pour commencer Cette valeur sera multipliée par n, avec n allant de 1 à 10, pour calculer factorielle 10. Programme très simple. Alors pourquoi aller chercher plus loin?
Méthode récursive Deux étapes: Mise en place d'une procédure, d'une sorte de fonction; puis, Appel à la procédure en indiquant la valeur de la factorielle cherchée. Dans la procédure, on retrouve un appel à la procédure! Bizarre! La procédure est appelée pour n décroissante à partir de 10, avec critère d'arrêt à 1.

Voir Programmation de la fonction factorielle (explications détaillées: algorithme, Maple et Scheme)

Récursivité & permutations
La plupart des programmes de maths possèdent un package capable de calculer directement les permutations. Voyons comment réaliser un algorithme puis un programme pour faire la même chose.		Exemple Maple Combinat est un groupe de programmes dédiés aux calculs en combinatoire. Permute (3) liste toutes les permutations des nombres 1, 2 et 3.
Méthode itérative (classique) Utilisation de boucles, une pour chaque nombre. Vérification que les trois nombres sont bien différents; et Impression des trois nombres. La logique du programme est ultra simple. La seule véritable difficulté, lorsque la quantité de nombre à permuter devient grande, consiste à énumérer toute la litanie des exclusions pour signifier que tous les nombres sont différents les uns des autres.
Astuce! Pour s'en sortir facilement avec le test des différences, on va utiliser la formation d'un ensemble {…}, lequel ne tolère pas les redondances. Ce qui veut dire que si l'ensemble comporte moins d'éléments que la collection originales, c'est qu'il y a redondance d'éléments.
Méthode récursive Voir Algorithme de permutation La méthode récursive fonctionne un peu comme le serpent d'Ouroboros qui s'avale la queue. La procédure consiste en une boucle qui écrit successivement 1, 2 et 3 dans la matrice A. L'idée consiste à passer trois fois dans cette boucle pour écrire les nombres aux rangs successifs:1, 2 et 3. À chaque itération, le programme inscrit ce qu'il a en mémoire (print). Lorsque la procédure est appelée (mise en route) par la simple instruction R(1) indiquant que le n initial sera 1, elle se déroule en imprimant à l'écran les valeurs indiquées ci-contre, toutes les permutations de 1, 2 et 3. Ce qui est appréciable: ne devoir exclure tous les cas où des nombres se répètent. Surtout pour un grand nombre de valeurs.		etc.
Programme pour six nombres permutés. Voici le programme pour six valeurs. Attention à l'impression qui peut être très volumineuse. Par exemple pour six chiffres, c'est déjà: 6! = 720. Notez quelques différences purement formelles entre ce programme et celui-ci-dessus: terminaison par end; ou encore, print(A) qui a l'avantage de évite de lister chaque valeur.

Programmation de permutations spéciales avec l'instruction "permute"
	Utilisation des programmes de combinatoire de Maple. Exemple pour les nombre n de 127 à 132. N est la liste des chiffres de n (effet de l'instruction convert) PN est la liste des permutations des chiffres de n. Q est la liste des nombres formés à partir de permutations et du calcul des nombres restitués à partir des chiffres de chaque permutation.
Explication de l'instruction composée calculant la valeur des nombres permutés

Voir Instruction seq / Premiers permutables / Programmation – Index

Retour	Programmation – Index
Suite	Algorithmes rapides de permutation – Programmation Application à l'énumération des combinaisons Arbre fractal avec programmation Processing Parenthèses – Générateur et compteur de paires valides Programme de tri rapide avec Python Programme récursif de calcul de la somme des chiffres concaténés Programme récursif de calcul de puissances Programme récursif de calcul du mot Fibonacci Programme récursif de multiplication par additions Programme récursif pour la racine numérique Quantité de partitions – Programme
Voir	Menu en en-tête Tour de Hanoï Palindromes – Nombres Palindromes – Mots et phrases Programmation – En savoir un peu plus
Site	Qu'est-ce que la récursivité – Dev Info
Cette page	http://villemin.gerard.free.fr/aInforma/10Palind.htm